FY2012 Annual Report
Computational Neuroscience Unit
Professor Erik De Schutter

Abstract
We use computational, data-driven methods to study how neurons and microcircuits in the brain operate. We are interested in how fundamental properties, such as a neuron’s morphology and its excitability, interact with one another during common neural functions like information processing or learning. Most of our models concern the cerebellum as this brain structure has a relatively simple anatomy and the physiology of its main neurons has been studied extensively, allowing for detailed modeling at many different levels of complexity.
1. Staff
General services and neuroinformatics
- Ivan Raikov, Technical Staff
- Tsuyuki Nakabayashi, Research Administrator/ Secretary
- Sachie Matsuoka, Research Administrator/ Secretary (from March 2013)
Molecular modeling
- Weiliang Chen, Researcher
- Iain Hepburn, Technical Staff
- Anant Jain, Technical Staff (from September 2012)
- Cory Simon, Intern (May-August 2012)
Cellular modeling
- Sungho Hong, Group Leader
- Shiwei Huang, Researcher
- Akira Takashima, Researcher (from March 2013)
- Haroon Anwar, Technical Staff
- Hermina Nedelescu, Special Research Student
- Arwel Pritchard, Intern (June-August 2012)
Network modeling
- Tom Close, Researcher
-
Daqing Guo, Researcher (till September 2012)
-
Mario Negrello, Researcher (till August 2012)
- Shyam Kumar Sudhakar, Special Research Student
- Pascal Warnaar, Special Research Student (till July 2012)
Rotation students
- Mohamed Abdelhack, Rotation Student (2nd term 2012)
- Viktoras Lisicovas, Rotation Student (2nd term 2012)
2. Collaborations
- Theme: Cerebellar physiology, multiple themes
- Type of collaboration: Scientific collaboration and graduate program
- Researchers:
- Professor M. Giugliano, University of Antwerp, Belgium
- Professor D. Snyders, University of Antwerp, Belgium
- Joao Couto, University of Antwerp, Belgium
- Q. Robberecht, University of Antwerp, Belgium
- K. Veys, University of Antwerp, Belgium
- Theme: Spiking activity of monkey cerebellar neurons
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor H.P. Thier, University of Tübingen, Germany
- A. Ignashchenkova, University of Tübingen, Germany
- Dr. M. Junker, University of Tübingen, Germany
- A. Schmigdlin, University of Tübingen, Germany
- Theme: Molecular identification of cerebellar signaling pathways and cerebellar optogenetics
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor G.J. Augustine, Korea Institute for Science and Technology (KIST), Korea
- Professor K. Tanaka, Korea Institute for Science and Technology (KIST), Korea
- Dr. J. Kim, Korea Institute for Science and Technology (KIST), Korea
- Theme: Modeling of effects of ethanol on the cerebellum
- Type of collaboration: Joint research
- Researchers:
- Professor C.F. Valenzuela, University of New Mexico, United States of America
- Theme: Correlation of neurons linked to their excitability
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor S.A. Prescott, University of Toronto, Canada
- Dr. S. Ratté, University of Toronto, Canada
- Theme: Purkinje cell morphology and physiology, modeling
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor M. Häusser, University College London, United Kingdom
- Professor H. Cuntz, Goethe University Germany
- Professor A. Watt, McGill University, Canada
- Dr. A. Roth, University College London, United Kingdom
3. Activities and Findings
3.1 Neuroinformatics standards
A pipeline for simulator-independent network modeling
The ability to develop models of complex neural networks in a simulator independent manner has been a longstanding goal of the computational neuroscience community. An important reasons is because the effect of subtle differences in simulator implementations, for example the timing of spike propagation (Morisson et al. 2007), on the qualitative behavior of networks with complex neuronal models is unclear a priori. In addition, the relevance of constraints placed on model design by fundamental assumptions in the simulator architecture and features that are not available in all simulators, such as gap junctions and active dendritic compartments, has not been extensively studied. To begin to address such issues, we developed a pipeline to translate xml-based network model descriptions into code suitable for the NEURON and NEST simulators.
We implement this approach for a cerebellar cortex model defined using a custom declarative architecture, based on NineML and NeuroML 2.0 where possible, and otherwise extended to meet the requirements of the model. Neuronal dynamics are described using a custom extension to the NineML language for conductance-based dynamics, which is compiled directly into simulator-native model formats (Raikov and De Schutter 2012). Connections between neuronal populations within the model are generated from a combination of morphologically based and soma-to-soma geometric connectivity rules. These rules are integrated into PyNN framework (Davison et al. 2008), which handles all the appropriate simulator-dependent connection routines. Where required by the NEURON simulator model, cell morphologies and gap junction connectors for the NEURON simulator are constructed by custom extensions to the PyNN framework, where the morphologies are built from descriptions in the NeuroML 2 morphology format.
In previous modeling, the behavior of the cerebellar granular layer sub-network has been shown to be strongly affected by the Golgi-to-Golgi gap junctions (de Souza and De Schutter 2011), making the cerebellar cortex an interesting system in which to study the implications of different implementations of gap junction connections. Therefore, the differences between the NEURON and NEST implementations of the cerebellar cortex model should lend considerable insight into the practical issues that could limit the development of truly simulator independent models.
3.2 Molecular mechanisms of synaptic plasticity
STEPS software development
Important new features were added to the stochastic reaction-diffusion simulator STEPS (Hepburn et al. 2012), resulting in the release of STEPS 2.0 in April 2013. The most important addition was the EField object to compute the membrane potential on the same tetrahedrical mesh in which the stochastic reaction-diffusion mechanisms are modeled (Hepburn et al. 2013). The tight and accurate integration of membrane potential calculation with the Stochastic Simulation Algorithm (SSA, Gillespie 1977) allowed for the investigation of stochastic calcium spikes in Purkinje cell dendrites described in section 3.3. In this scheme both channel gating and charge transitions through the channel pore can be fully stochastic. Next we strongly improved the deterministic modeling in STEPS by integrating the standard CVODE module (Cohen and Hindmarsh 1996) as one of the soultion engines. The STEPS implementation allows different some parts of the model to be run stochastically and other ones to be run deterministically. This hybrid modeling approach is a very effective way to identify the sources of stochasticity in complex systems (Anwar et al. 2013).
The role of dendritic spine morphology in compartmentalizing surface receptors
Since AMPA receptors are major molecular players in both short- and long-term plasticity, it is important to identify the time-scales of and factors affecting the lateral diffusion of AMPARs on the dendrite surface. Using a mathematical model, we studied how the dendritic spine morphology affects two processes: (1) compartmentalization of the surface receptors in a single spine to retain local chemistry and (2) the delivery of receptors to the post-synaptic density (PSD) of spines via lateral diffusion following insertion onto the dendrite shaft. Computing the mean first passage time (MFPT) of surface receptors on a sample of real spine morphologies revealed that a constricted neck and bulbous head serve to compartmentalize receptors, consistent with previous studies (Holcman and Schuss 2011). We found that the location of the PSD corresponds to the location at which the maximum MFPT occurs, the position that maximizes the residence time of a diffusing receptor.
Meanwhile, the same geometric features of the spine that compartmentalize receptors inhibit the recruitment of AMPARs via lateral diffusion from dendrite insertion sites. Spines with narrow necks will trap a smaller fraction of diffusing receptors in the their PSD when considering competition for receptors between the spines, suggesting that ideal geometrical features involve a tradeoff depending on the intent of compartmentalizing the current receptor pool or recruiting new AMPARs in the PSD. The ultimate distribution of receptors among the spine PSDs by lateral diffusion from the dendrite shaft is an interplay between the insertion location and the shape and locations of both the spines and their PSDs.
Probabilistic induction of cerebellar long-term depression
Many cellular processes involve a small number of molecules and undergo stochastic fluctuations in their levels of activity. Cerebellar long-term depression (LTD) is a form of synaptic plasticity expressed as a reduction in the number of synaptic AMPARs in Purkinje cells. We developed a stochastic model of the LTD signaling network, including a PKC-ERK-cPLA2 positive feedback loop and mechanisms of AMPAR trafficking, and tuned the model to replicate calcium uncaging experiments (Antunes and De Schutter 2012).
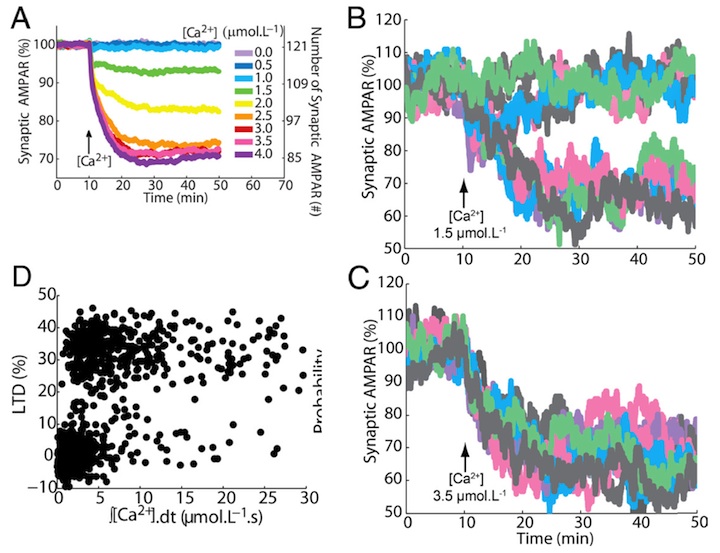
Figure 1: (A) Averaged output of the stochastic model: a graded reduction of the number of AMPARs depending on the amplitude of the calcium stimulus accurately replicates experimental LTD data (Tanaka et al. 2007). (B, C) In single spines (or single trial of the model) the response is bistable: each color represents a different run of the model. For a low calcium stimulus both non-LTD and LTD are observed (B), for a high stimulus only LTD (C). (D) These responses are probabilistic: the integrated stimulus calcium concentraion shows no clear threshold for LTD induction. Replicated from Antunes and De Schutter (2012).
The signaling network activity in single synapses switches between two discrete stable states (LTD and non-LTD, Figure 1B-C) in a probabilistic manner. The stochasticity of the signaling network causes threshold dithering and allows at the macroscopic level for many different and stable mean magnitudes of depression (Figure 1A). The probability of LTD occurrence in a single spine is only modulated by the concentration and duration of the signal used to trigger it, and inputs with the same magnitude can give rise to two different responses; there is no threshold for the input signal (Figure 1D). The stochasticity is intrinsic to the signaling network and not mostly dependent on noise in the calcium input signal, as has been suggested previously.
The activities of the ultrasensitive ERK and of cPLA2 undergo strong stochastic fluctuations. Conversely, PKC, which acts as a noise filter, is more constantly activated. Systematic variation of the biochemical population size demonstrates that threshold dithering and the absence of spontaneous LTD depend critically on the number of molecules in a spine, indicating constraints on spine size in Purkinje cells.
3.3 Cellular mechanisms regulating firing and synaptic properties of neurons
Geometric theory predicts bifurcations in minimal wiring cost trees in biology are flat
The complex three-dimensional shapes of tree-like structures in biology are constrained by optimization principles, but the actual costs being minimized can be difficult to discern. We analyzed and found that despite quite variable morphologies and functions, bifurcations in the scleractinian coral Madracis and in many different mammalian neuron types tend to be planar (Kim et al. 2012). We have proves that in fact bifurcations embedded in a spatial tree that minimizes wiring cost should lie on planes. This biologically motivated generalization of the classical mathematical theory of Euclidean Steiner trees is compatible with many different assumptions about the type of cost function. Since the geometric proof does not require any correlation between consecutive planes, we predicted that, in an environment without directional biases, consecutive planes would be oriented independently of each other. This was confirmed for many branching corals and neuron types. Consequently, it seems that planar bifurcations are characteristic of wiring cost optimization in any type of biological spatial tree structure.
3.4 Information processing in the olivocerebellar system
Complex spike waveforms in the awake monkey are determined by the interval to the previous complex spikeStrong controversy exists about the role of complex spikes in cerebellar Purkinje cells. The olivocerebellar system may be a generator of temporal motor patterns based on subthreshold oscillation in the inferior olive. Alternatively, the complex spike can act as a teacher or error signal and control plasticity of the parallel fiber synapses onto the Purkinje cell.
Complex spikes come in different shapes which are influenced by the state of the Purkinje cell and by bursting activity in the climbing fiber input. The waveform therefore could harbor coding information, reflecting conditions in different parts of the olivo-cerebellar system. The shape of the complex spikes can influence intracellular calcium levels in the Purkinje cell, which are critically involved in plasticity or can influence the output to the cerebellar nuclei.
We studied complex spike waveforms are described for the first time in the awake monkey, based on 50 extracellular recordings, spanning more than an hour each. In total over 3000 complex spikes from 10 different Purkinje cells were analyzed and described in respect of their stable variations of shape. On average a single Purkinje cell shows 12±5 stable waveform shapes. Overall, the +3000 complex spikes had 2 to 9 spikelets. The number of spikelets as well as onsets of the spikelets in different complex spike stable waveforms were analyzed. We found a significant correlation between the presence of specific stable waveforms and the preceding inter complex spikes interval length in many recordings, with the last spikelet of the complex spike being more delayed for short intervals to the preceding complex spike.
3.5 References cited
- Antunes G, De Schutter E (2012) A stochastic signaling network mediates the probabilistic induction of cerebellar long-term depression. Journal of Neuroscience 32: 9288-9300.
- Anwar H, Hong S, De Schutter E. (2012) Controlling Ca2+-activated K+ channels with models of Ca2+ buffering in Purkinje cells. Cerebellum 11: 681-693.
- Anwar H, Hepburn I, Nedelescu H, Chen W, De Schutter E (2013) Stochastic calcium mechanisms cause dendritic calcium spike variability. Submitted.
- Cohen SD, Hindmarsh AC (1996) CVODE, A Stiff/Nonstiff ODE Solver in C. Computers in Physics 10: 138-143.
- Davison AP et al.: PyNN: a common interface for neuronal network simulators. Frontiers in Neuroinformatics 2008, 2:11.
- de Souza FMS, De Schutter E (2011) Robustness effect of gap junctions between Golgi cells on cerebellar cortex oscillations. Neural Systems & Circuits 1: 7.
- Hepburn I, Chen W, Wils S, De Schutter E (2012) STEPS: efficient simulation of stochastic reaction-diffusion models in realistic morphologies. BMC Systems Biology 6: 36.
- Hepburn I, Cannon R, De Schutter E (2013 ) Efficient calculation of the quasi-static electrical potential on a tetrahedral mesh and its implementation in STEPS. Submitted.
- Holcman D, Schuss Z (2011) Diffusion laws in dendritic spines. Journal of Mathematical Neuroscience 1:10.
- Inagaki N et al. (2007) Separate oscillating cell groups in mouse suprachiasmatic nucleus couple photoperiodically to the onset and end of daily activity. Proceedings of the National Academy of Sciences USA 104: 7664 –7669.
- Kim Y et al. (2012) Geometric theory predicts bifurcations in minimal wiring cost trees in biology are flat. PLoS Computational Biology 8: e1002474.
- Morrison A et al: Exact subthreshold integration with continuous spike times in discrete-time neural network simulations. Neural Computation 19: 47–79.
- Myung J et al. (2012) Period coding of Bmal1 oscillators in the suprachiasmatic nucleus. Journal of Neuroscience 32: 8900-8918.
- Raikov I, De Schutter E (2012) The Layer-Oriented Approach to Declarative Languages for Biological Modeling. PLoS Computational Biology 8: e1002521.
-
Tanaka K et al. (2007) Ca2+ requirements for cerebellar long-term synaptic depression: role for a postsynaptic leaky integrator. Neuron 54: 787– 800.
4. Publications
4.1 Journals
- Antunes, G. & E. De Schutter (2012). "A stochastic signaling network mediates the probabilistic induction of cerebellar long-term depression." J Neurosci 32(27): 9288-9300.
- Anwar, H., Hong, S. & De Schutter, E. (2012). "Controlling Ca2+-activated K+ channels with models of Ca2+ buffering in Purkinje cells." Cerebellum 11(3): 681-693.
- Botta, P., Simoes de Souza, F.M., Sangrey, T., De Schutter, E. & Valenzuela, C.F. (2012). "Excitation of rat cerebellar Golgi cells by ethanol: further characterization of the mechanism." Alcohol Clin Exp Res 36(4): 616-624.
- Diaz, M. R., Wadleigh, A., Kumar, S., De Schutter, E. & Valenzuela, C.F. (2013). "Na+/K+-ATPase Inhibition Partially Mimics the Ethanol-Induced Increase of the Golgi Cell-Dependent Component of the Tonic GABAergic Current in Rat Cerebellar Granule Cells." PLoS One 8: e55673.
- De Schutter, E. (2012). "The importance of stochastic signaling processes in the induction of long-term synaptic plasticity." Neural Networks 36: Epub ahead of print.
- De Schutter, E., Ascoli, G.A. & Kennedy D.N. (2012). "Ten years of neuroinformatics." Neuroinformatics 10(4): 329-330.
- Hong, S., Robberechts, Q. & De Schutter, E. (2012). "Efficient estimation of phase-response curves via compressive sensing." J Neurophysiol 108(7): 2069-2081.
- Kim, Y., Sinclair, R., Chindapol, N., Kaandorp, J.A. & De Schutter, E. (2012). "Geometric theory predicts bifurcations in minimal wiring cost trees in biology are flat." PLoS Comput Biol 8(4): e1002474.
- Myung, J., Hong, S., Hatanaka, F., Nakajima, Y., De Schutter, E. & Takumi, T (2012). "Period coding of Bmal1 oscillators in the suprachiasmatic nucleus." J Neurosci 32(26): 8900-8918.
- Raikov, I. & E. De Schutter (2012). "The layer-oriented approach to declarative languages for biological modeling." PLoS Comput Biol 8(5): e1002521.
- Veys, K., Labor, A.J., De Schutter, E. & Snyders, D.J. (2012). "Quantitative single-cell ion-channel gene expression profiling through an improved qRT-PCR technique combined with whole cell patch clamp." J Neurosci Methods 209(1): 227-234.
4.2 Books and other one-time publications
Nothing to report
4.3 Oral Presentations
- De Schutter, E. (2012). Challenges of simulator-independent network modeling. Cosyne 2013 Workshops, , Large-scale neuronal simulations - science, languages, and platforms, Snow Bird, Utah, USA.
- De Schutter, E. (2012). Stochastic processes in Purkinje cell spines and dendrites. C7 + CEREBRATE ITN networks meeting, Amsterdam, Netherlands.
- De Schutter, E. (2012). An Introduction to Cerebellar Physiology and Function. IBITA Educational Day: Cerebellar function and pathology, Leuven, Belgium.
- De Schutter, E. (2012). Stochastic processes in spines and dendrites during learning. Annual meeting of Korean Society for Computational Neuroscience, Seoul, Korea.
- De Schutter, E. (2012). Introduction to neuroinformatics and data sharing. Computational Neuroscience Workshop on Behavior Informatics, Decatur, GA, USA.
- De Schutter, E. (2012). A stochastic signaling network mediates probabilistic induction of cerebellar synaptic plasticity. Workshop on Computational Neuroscience, Brain Science Institute, RIKEN, Japan.
- De Schutter, E. (2012). Data publication to improve data sharing. INCF Nodes Workshop, International Neuroinformatics Coordination Facility, Stockholm, Sweden.
- Hong, S. (2012). Single neuron firing properties impact correlation-based population coding. Workshop on Computational Neuroscience, Brain Science Institute, RIKEN, Japan.
4.4 Poster Presentation
- Hepburn, I., et al. (2012). A computational study of stochastic mechanisms in dendritic calcium spike generation. FENS Forum 2012. Barcelona, Spain.
- Nedelescu, H., et al. (2012). Visualizing the developing Purkinje cell dendritic forest using multicolor Brainbow mice. FENS Forum 2012. Barcelona, Spain.
- Negrello, M., et al. (2012). Reins and slingshots: contributions of cerebellar pauses to saccadic eye movements. FENS Forum 2012. Barcelona, Spain.
- Sudhakar, S. K., et al. (2012). A modeling study of how inhibition spreads through molecular layer gap junctions in the cerebellar cortex. FENS Forum 2012. Barcelona, Spain.
- Warnaar, P. and E. De Schutter (2012). A Purkinje cell in the awake monkey produces multiple stable complex spike waveforms. FENS Forum 2012. Barcelona, Spain.
- Anwar, H., et al. (2012). A computational study of stochastic mechanisms in dendritic calcium spike generation. CNS 2012 meeting. Atlanta/ Dcatur GA, USA.
- Chen, W. and E. De Schutter (2012). Improving Data Caching of the STochastic Engine for Pathway Simulation (STEPS). CNS 2012 meeting. Atlanta/ Decatur GA, USA.
- Close, T. G., et al. (2012). Exploring the functional implications of brain architecture and connectivity: a multi-simulator framework for biophysical neuronal models. CNS 2012 meeting. Atlanta/Decatur GA, USA.
- Guo, D., et al. (2012). A computational study on the spatial correlation of granule cell firing in the cerebellar cortex. CNS 2012 meeting. Atlanta/ Decatur GA, USA.
- Raikov, I., et al. (2012). Exploring the functional implications of brain architecture and connectivity: a declarative language framework. CNS 2012 meeting. Atlanta/Decatur GA, USA.
- Anwar, H., et al. (2012). A computational study of molecular mechanisms underlying variability of dendritic calcium spikes. Society for Neuroscience 2012. New Orleans, USA.
- Nedelescu, H., et al. (2012). Tracking anatomical changes in the maturing Purkinje cell dendritic forest. Society for Neuroscience New Orleans, USA.
- Hong, S., et al. (2013). Behavior-modulated correlation of cerebellar Purkinje neuron and network activity. COSYNE 2013. Saltlake City, USA.
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Summer Course
Okinawa Computational Neuroscience Course 2012
- Date : June 11 – June 28, 2011
- Venue : Seaside House, OIST
- Co-organizers: E. De Schutter, K. Doya & J. Wickens, OIST
- Speakers
- Abbott, Larry (Columbia University)
- Arbuthnott, Gordon (OIST)
- Bialek, William (Princeton University)
- Buzsaki, Gyorgy (New York University, School of Medicine)
- Canavier, Carmen (Department of Cell Biology and Anatomy LSU Health Sciences Center)
- De Schutter, Erik (OIST)
- Diesmann, Markus (Institute of Neuroscience and Medicine)
- Doya, Kenji (OIST)
- Häusser, Michael (University College London)
- Ishii, Shin (Kyoto University)
- Izhikevich, Eugene (Brain Corporation)
- Kuhn, Bernd (OIST)
- Lee, Daeyeol (Yale University School of Medicine)
- Marder, Eve (Brandeis University)
- Stephens, Greg (OIST)
- Yazaki-Sugiyama, Yoko (OIST)
6.2 Winter Course
Course in Molecular Neuroanatomy 2013
- Date : January 27 – February 8, 2013
- Venue : Seaside House, OIST
- Co-sponsor: The Allen Institute for Brain Science
- Co-organizers: E. De Schutter, T. Gilbert & J. Hohmann
- Speakers:
- Gordon Arbuthnott (OIST)
- Erik De Schutter (OIST)
- Terri Gilbert (AIBS)
- John Hohmann (AIBS)
- Chris Lau (AIBS)
- Luis Puelles (University of Murcia, Spain)
- George Paxinos (Monash University, Australia)
- Josh Royal (AIBS)
- John Rubenstein (University California San Francisco, USA)
- Charles Watson (Monash University, Australia)
6.3 Seminars
Microelectronic system for high-resolution mapping of extracellular electric fields applied to brain slices
- Date: April 12th, Thursday / 16:00-17:00
- Venue: Campus Lab1 Level D, Meeting room D014
- Speaker: Dr. Urs Frey, the RIKEN Quantitative Biology Center in Kobe



