FY2020 Annual Report
Computational Neuroscience Unit
Professor Erik De Schutter

See names on each tile, Dr. Sergio Verduzco is the unnamed person.
Abstract
We use computational, data-driven methods to study how neurons and microcircuits in the brain operate. We are interested in how fundamental properties, such as a neuron’s nanoscale morphology and its excitability, interact with one another during common neural functions like information processing or learning. Most of our models concern the cerebellum as this brain structure has a relatively simple anatomy and the physiology of its main neurons has been studied extensively, allowing for detailed modeling at many different levels of complexity. More recently we have also built models of hippocampal synapses.
1. Staff
- Molecular modeling
- Iain Hepburn, Technical Staff
- Andrew Gallimore, Staff Scientist
- Sarah Yukie Nagasawa, PhD Student
- Cellular modeling
- Sungho Hong, Group Leader
- Alexey Martyushev, Postdoctoral scholar
- Gabriela Capo Rangel, Postdoctoral scholar
- Audrey Denizot, Postdoctoral scholar
- Network modeling
- Sergio Verduzco, Postdoctoral scholar (till October 2020)
- Mykola Medvidov, Staff Scientist (till September 2020)
- Mizuki Kato, PhD Student
- Software development
- Weiliang Chen, Staff Scientist
- Jules Lallouette, Postdoctoral scholar
- Visiting Researcher
- Jihwan Myung, Taipei Medical University
- Samuel Melchior, EPFL
- Tristan Carel, EPFL
- Fernando Pereira, EPFL
- Giacomo Castiglioni, EPFL
- Yoshiyuki Asai, Yamaguchi University Graduate School of Medicine
- Yunliang Zang, Brandeis University
- Visiting Research Student
- Taro Yasuhi,Yamaguchi University School of Medicine
- Research Interns
- Haruki Shigeta, Tohoku University School of Medicine
- Rotation Students
- Mariia Pavelchenko (Term 1)
- Hugo Musset (Term 2)
- Javier Andrés Tejeda Mora (Term 2)
- Research Unit Administrator
- Chie Narai
2. Collaborations
- Theme: Cerebellar physiology, multiple themes
- Type of collaboration: Scientific collaboration and graduate program
- Researchers:
- Professor M. Giugliano, University of Antwerp, Belgium and SISSA, Italy
- Professor D. Snyders, University of Antwerp, Belgium
- Theme: Spiking activity of monkey cerebellar neurons
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor H.P. Thier, University of Tübingen, Germany
- Akshay Markanday, University of Tübingen, Germany
- Junya Inoue, University of Tübingen, Germany
- Peter Dicke, University of Tübingen, Germany
- Theme: Human Brain Project: simulator development
- Type of collaboration: Scientific collaboration
- Researchers:
- Prof. F. Schürmann, École Polytechnique Fédérale de Lausanne, Switzerland
- Dr. T. Carel, École Polytechnique Fédérale de Lausanne, Switzerland
- Dr. G. Castiglioni, École Polytechnique Fédérale de Lausanne, Switzerland
- Dr. F. Pereira, École Polytechnique Fédérale de Lausanne, Switzerland
- Theme: Molecular identification of cerebellar signaling pathways and cerebellar optogenetics
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor K. Tanaka, Korea Institute for Science and Technology (KIST), Korea
- Professor K. Tanaka, Korea Institute for Science and Technology (KIST), Korea
- Theme: Quantitative molecular identification of hippocampal synapses
- Type of collaboration: Scientific collaboration
- Researchers:
- Prof. Dr. Silvio O. Rizzoli, Medical University Göttingen, Germany
- Theme: Cerebellar molecular layer interneurons
- Type of collaboration: Joint research
- Researchers:
- Professor Alain Marty, Université Paris 5 René Descartes, France
- Theme: Cerebellar anatomy and physiology
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor C. De Zeeuw, Erasmus Medical Center, Rotterdam, The Netherlands
- Professor L.W.J. Bosman, Erasmus Medical Center, Rotterdam, The Netherlands
- Dr. M. Negrello, Erasmus Medical Center, Rotterdam, The Netherlands
- Theme: Purkinje cell morphology and physiology, modeling
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor M. Häusser, University College London, United Kingdom
- Professor A. Roth, University College London, United Kingdom
- Dr. S. Dieudonné, Ecole Normale Supérieure, Paris, France
- Theme: Circadadian rhythm generation
- Type of collaboration: Scientific collaboration
- Researchers:
- Professor J. Myung, Taipei Medical University, Taiwan
3. Activities and Findings
3.1 Software Development
Pycabnn: software to construct an anatomical basis for a physiologically realistic neural network model
Physiologically detailed models of neural networks are an important tool for studying how biophysical mechanisms impact neural information processing. An important, fundamental step in constructing such a model is determining where neurons are placed and how they connect to each other, based on known anatomical properties and constraints given by experimental data. We developed an open-source software tool, Pycabnn, that is dedicated to generating an anatomical model, which serves as the basis of a full network model (Wichert et al., 2020). We implemented efficient algorithms for generating physiologically realistic cell positions and for determining connectivity based on extended geometrical structures such as axonal and dendritic morphology.
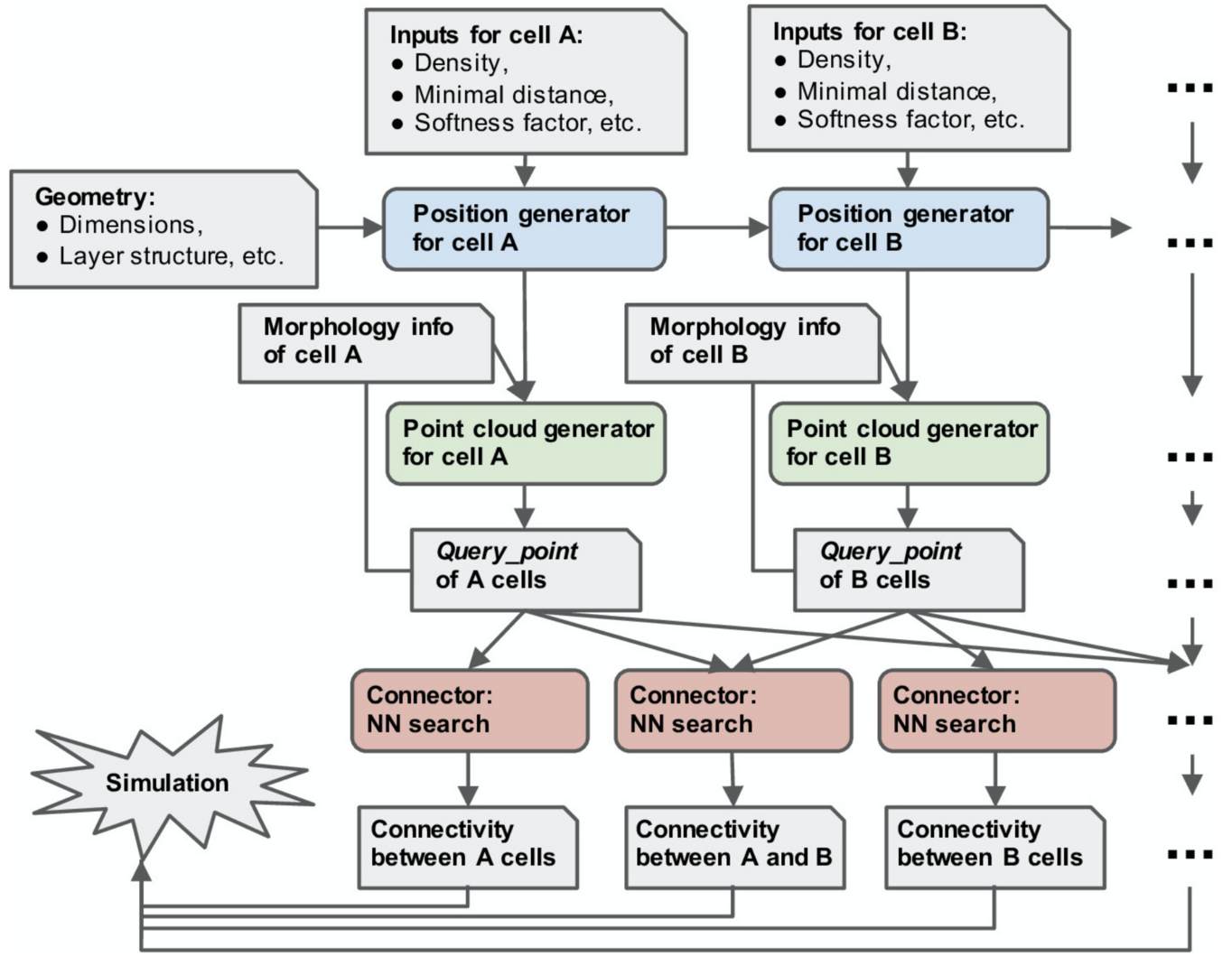
Figure 1: overview of the structure of pycabnn. After sequentially generating cell body positions of given neuron types (blue), point clouds representing morphological structures are generated (green) and stored in Query_point data structures with other information for simulation. Those Query_point data are then fed into Connector’s (red) that perform the nearest neighbor search and generate connectivity data in a format that a simulator can take as an input (from Wichert et al., Frontiers in Neuroinformatics 2020).
The capabilities and performance of Pycabnn were demonstrated by a network model of the cerebellar granular layer, which requires generating more than half a million cells and computing their mutual connectivity (Figure 2).
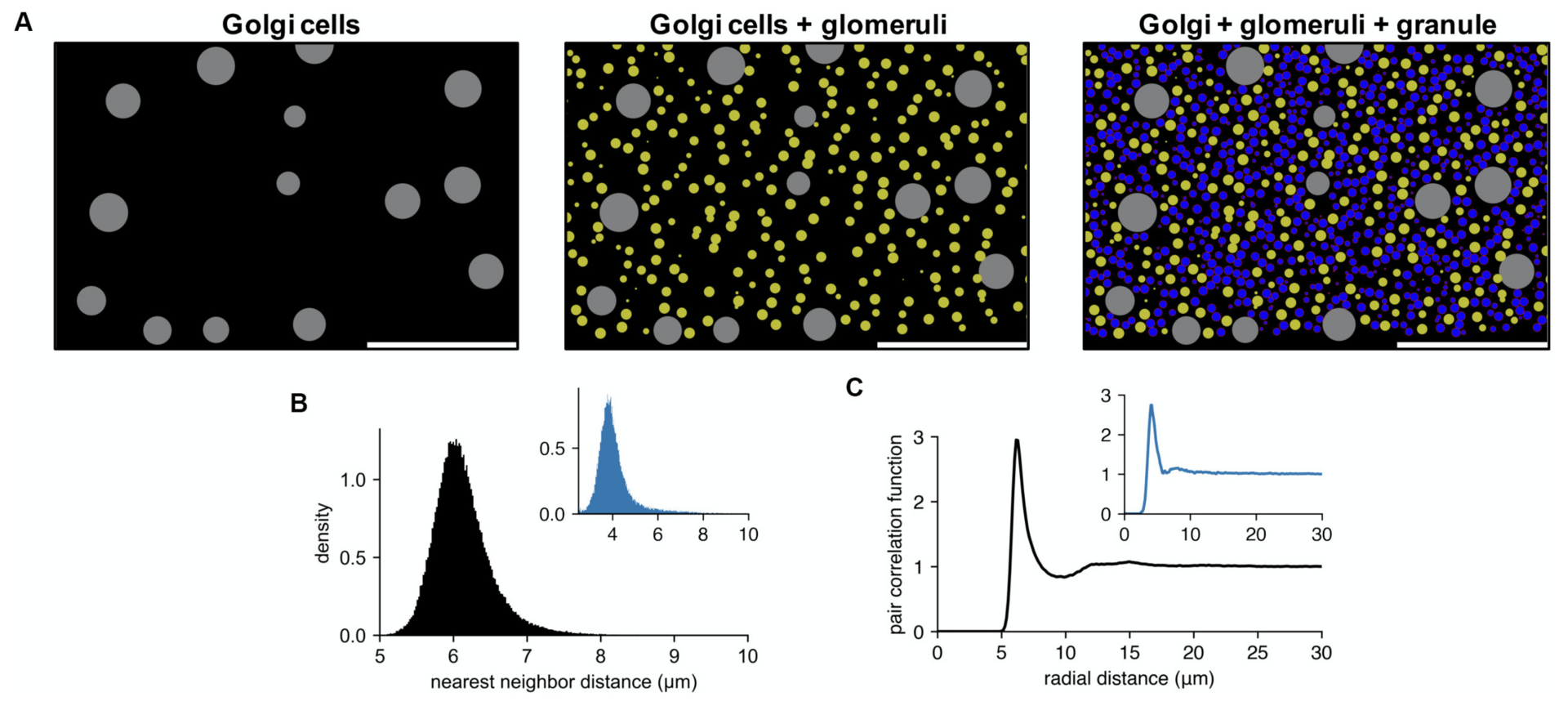
Figure 2: example of cell locations in a cerebellar granular layer network model. (A) Sequential generation of Golgi cells (left), glomeruli (middle), and granule cells (right) in a model of the granular layer in the rodent cerebellum. A small fraction of the cells is shown in a sagittal plane (x: sagittal, y: vertical direction). Scale bar: 100 μm. Physiological diameters (Golgi: 27 μm; Glomerulus: 8.39 μm; Granule: 6.15 μm) and density parameters (Billings et al., Neuron 2014; Sudhakar et al., PLoS Comp. Biol. 2017) are used. (B,C). Nearest neighbor distribution (B) and pair correlation function (C) of the model granule cells. Insets are based on experimental data from human cerebellum (Töpperwien et al., PNAS 2018). Peak locations are different in insets since they are based on human data where the granule cells are smaller ([diameter: 4.00 ± 0.02 μm (Töpperwien et al., 2018)] (from Wichert et al., 2020).
Pycabnn is efficient enough to carry out all the required tasks on a laptop computer within reasonable runtime, although it can also run in a parallel computing environment. Written purely in Python with limited external dependencies, pycabnn is easy to use and extend, and it can be a useful tool for computational neural network studies in the future.
3.2 Cellular mechanisms regulating firing and synaptic properties of neurons
Purkinje cell phase responses support transient oscillations
Both spike rate and timing can transmit information in the brain. Phase response curves (PRCs) quantify how a neuron transforms input to output by spike timing. PRCs exhibit strong firing-rate adaptation, but its mechanism and relevance for network output are poorly understood. In cerebellar Purkinje cells (PCs), phase responses to weak stimuli at low firing rates are small and surprisingly flat. With increased rates, responses in later phases become phase-dependent, with earlier onset-phases and gradually increasing peak amplitudes (Phoka et al., PLoS Comp. Biol. 2010; Couto et al., PLoS Comp. Biol. 2015).
This PRC property has never been theoretically replicated or explained, nor has its effect on synchronizing spike outputs been explored. We found that our recent PC model (Zang et al., Cell Reports 2018) reproduces this behavior well (Zang et al. eLife 2020; Figure 3).

Figure 3: PRC exhibits strong rate adaptation in PC model. (A) Schematic representation of the definition and computation of PRCs. The current pulse has a duration of 0.5 ms and an amplitude of 50 pA. Different spike rates were achieved by somatic current injection. (B) The rate adaptation of the flat part and the phase-dependent PRC peak. (C) PRC peak amplitudes at different firing rates fitted by the Boltzmann function. (D) Duration of the flat phase at different firing rates (from Zang et al., 2020).
Using our PC model, we demonstrate that the rate adaptation is caused by rate-dependent subthreshold membrane potentials efficiently regulating the activation of Na+ channels (not shown).
Next we asked whether these PRC properties could form the basis of high-frequency oscillations that have been observed in the PC layer of the adult cerebellar cortex (de Solages et al., Neuron 2008). We use a realistic PC network model to examine how rate-dependent responses synchronize spikes in the scenario of reciprocal inhibition-caused high-frequency oscillations (Figure 4). The network shows intermittent pairwise synchrony on the population level rather than spike-to-spike synchrony (Figure 4B). The changes in PRC cause oscillations and spike correlations only at high firing rates: 70 and 116 Hz in Figure 4D, not at low firing rates (10 Hz). The causal role of the PRC was confirmed using a simpler coupled oscillator network model (not shown).
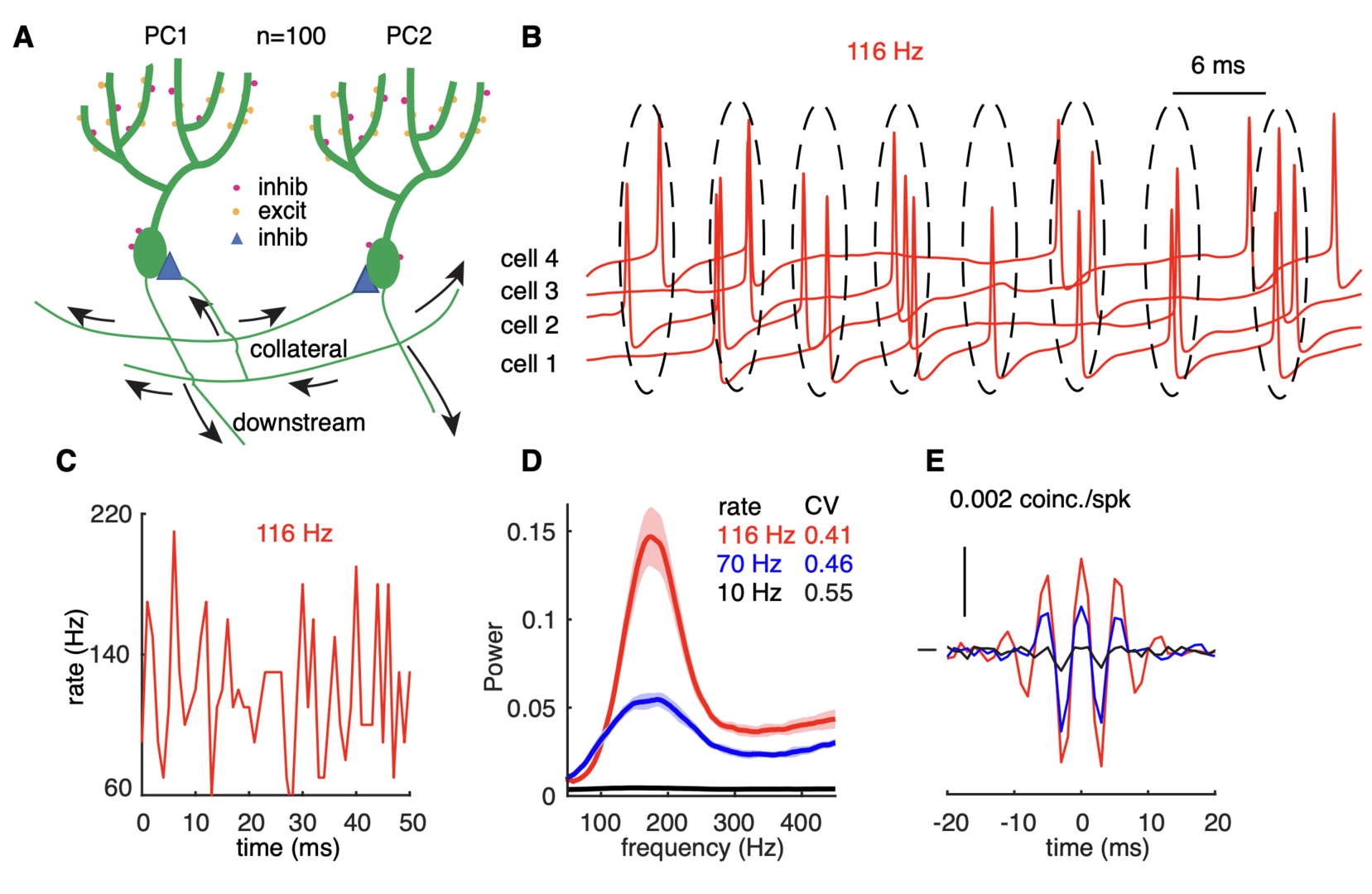
Figure 4: high-frequency oscillations show adaptation to cellular firing rates. (A) Schematic representation of the network configuration: synaptically excited PCs inhibit each other. (B) Example of sampled PC voltage trajectories in the network with clusters of intermittent population synchrony indicated. (C) Example of population rates in the network (time bin 1 ms). (D) The power spectrum of population rates of the network at different cellular rates and firing irregularity (CV of ISIs). (E) average normalized cross-correlograms between PC pairs at different cellular rates (from Zang et al., 2020).
Because the synchronizing mechanism depends on PC firing rates, we expect that it can be turned on and off relatively fast enabling transient oscillations between PCs. This was confirmed when population rates of the network were changed by the half-positive cycle of a 1 Hz sine wave (Figure 5A). The main and the third diagonals of the joint peristimulus time histograms matrix, corresponding to 0 ms-time lag correlation and 6 ms-time lag correlation respectively, are plotted to show the dynamic synchrony at transiently increased rates (bin size is 2 ms, Figure 5B). At low basal rates, there are no correlations between spikes. Both correlations start to increase ~250 ms after the onset of simulations when the cellular firing rate increases. Closely following rate changes, they decrease again when the cellular rates drop. It demonstrates that axon collateral-caused spike correlations can be achieved transiently, forming PC assemblies, to transmit a correlation code conjunctive with temporal cellular firing rate increases. Robust assembly formation occurred only between fast firing PCs when there were also slower firing PCs in the network (not shown).

Figure 5: correlations can be transient and robust to heterogeneous spike rates. (A) Population spike rates of PCs in the network. (B) The 0 ms- and 6 ms-time lag correlations between PCs increase with population rates (from Zang et al., 2020).
The results suggest that a population of PCs with increased spike rates can form a correlated assembly that will strongly affect downstream neurons even when it is surrounded by non-correlated neighboring PCs with decreased spike rates.
3.3 Information processing in neural networks
Lamina-specific neuronal properties promote robust, stable signal propagation in feedforward networks
Feedforward networks (FFN) are ubiquitous structures in neural systems and have been studied to understand mechanisms of reliable signal and information transmission. In many FFNs, neurons in one layer have intrinsic properties that are distinct from those in their pre-/postsynaptic layers, but how this affects network-level information processing remains unexplored.
We show that layer-to-layer heterogeneity arising from lamina-specific cellular properties facilitates signal and information transmission in FFNs (Han et al., NeurIPS 2020). Specifically, we found that signal transformations, made by each layer of neurons on an input-driven spike signal, demodulate signal distortions introduced by preceding layers (Figure 6).
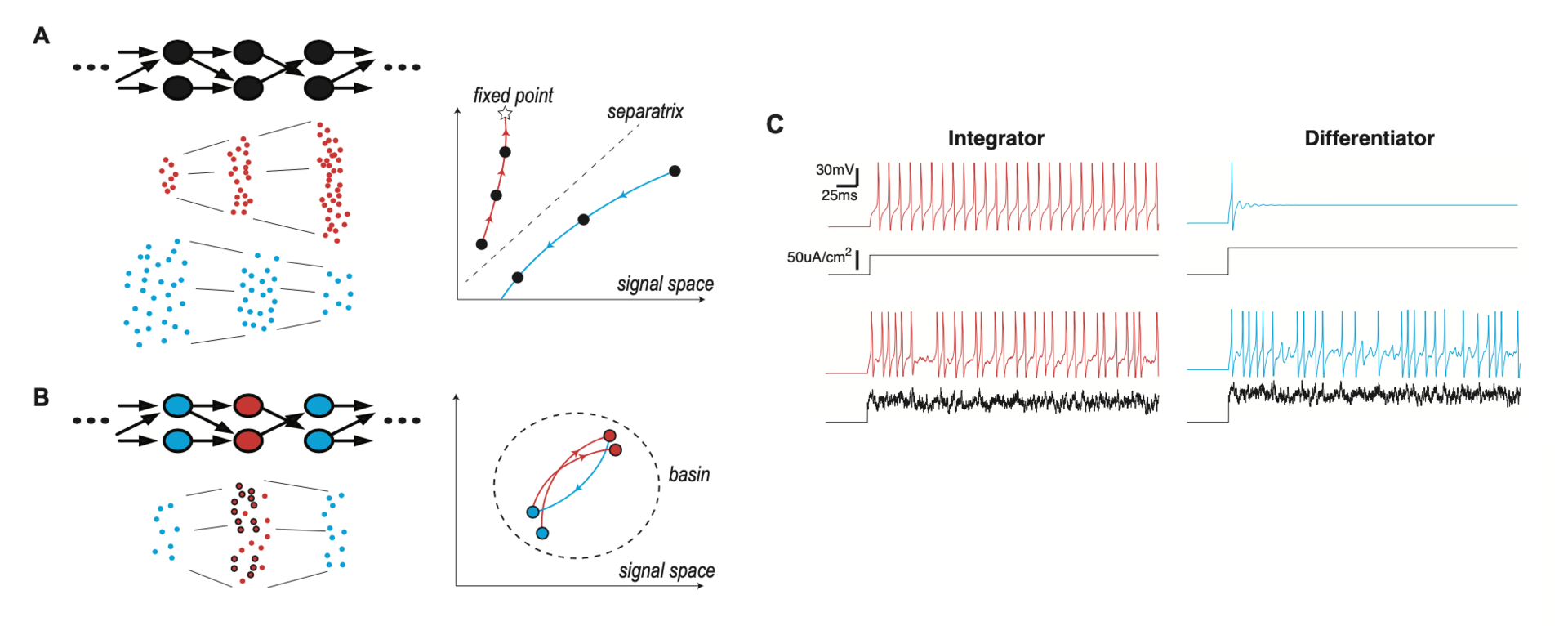
Figure 6: lamina-specific neuronal properties stabilize signal transmission in a network. (A) Left: FFN with a single cell type (Top), and spikes at each layer, in two different modes of signal propagation (Bottom). One mode is amplification by progressively evoking more and more synchronized spikes (red dots) and the other is dissipation by gradually losing spikes (blue dots). Right: Trajectories of the two propagating signals, in signal space. The x- and y-axes represent the total spike count and temporal width of the propagating signal, respectively. The star is a fixed point of signal transformation by individual layers, and the dotted line is a separatrix separating the two modes. (B) Left: FFN where neurons have lamina-specific intrinsic properties (Top). The right layer (blue) performs a compensatory transformation that selectively transforms a subset of input spikes (circled red dots), demodulating signal distortions introduced by the presynaptic middle layer (red) (Bottom). Right: Trajectory of the propagating signal in the signal space. The dotted circle is a region (basin) where the propagating signal is stabilized by compensating transformations (C) Membrane potential response (color) to constant or fluctuating current injection (black) for integrator and differentiator neuron models. (from Han et al., 2020).
This mechanism boosts information transfer carried by a propagating spike signal and thereby supports reliable spike signal and information transmission in a FFN. Using neural layers with such laminar specificity, we developed a model of the Drosophila antennal lobe network with three layers (not shown). We show that this model replicates key findings of a recent experimental study on optimal information transfer in a FFN (Jeanne and Wilson, Neuron 2015).
We then investigated whether this mechanism can also enhance signal transmission in larger networks. For this purpose, we extended the network to a deep heterogeneous FFN model by adding alternating layers of integrator or differentiator neurons. The deep FFN models had nine layers of 1,000 differentiator or integrator neurons, except for the input layer comprising differentiators. Each neuron was randomly connected to nine presynaptic neurons on average. We simulated how a packet of spikes, injected into the input layer, propagates through subsequent layers (Diesmann et al., Nature 1999). Spike generators randomly sampled in total α spike times from a normal distribution with variance σ2 and forced the input layer neurons to fire at the spike times, in addition to noisy spontaneous firing.
We found that the spike signals stably propagated in this network (Figure 7), whereas homogeneous networks, with only differentiators or integrators, showed opposing results: In the all-differentiator network, the evoked spike signal became increasingly synchronized and propagated as layer-wide synchronized spikes. In contrast, in the all-integrator network, the evoked spike signal became broader and less synchronized, until it eventually dissipated into spontaneously firing spikes.
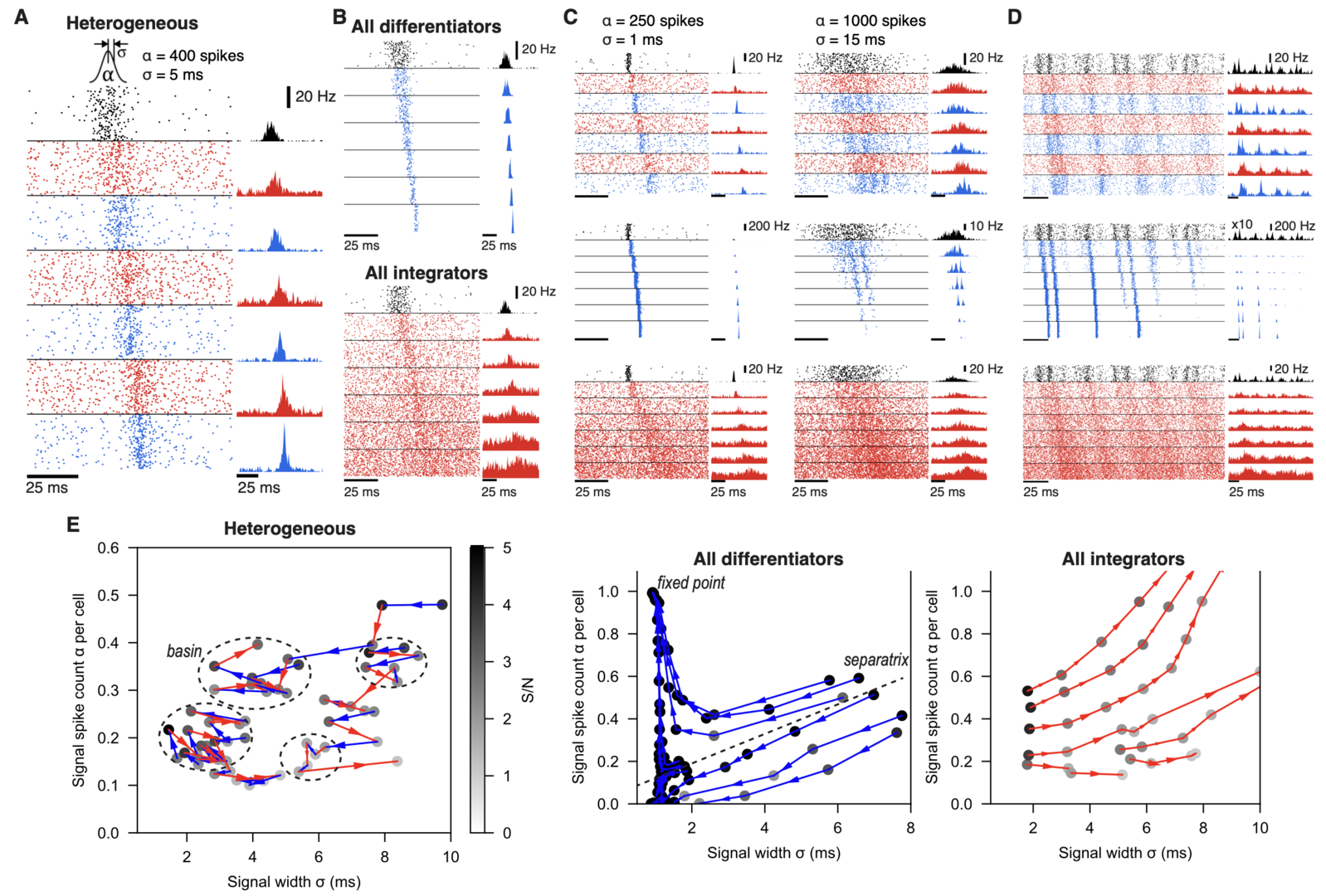
Figure 7: lamina-specific neuronal properties robustly stabilize spike signal propagation in deep FFNs. (A) Propagation in a heterogeneous network. Inset on top is the Gaussian distribution of spikes, evoked in the input layers (black). Dots (Left) and histograms (Right) are spikes and their firing rates, respectively. In all figures, blue and red represent differentiators and integrators, respectively. (B) Firing in homogeneous networks with only differentiators (Top) and integrators (Bottom). (C) Propagation of signals with different spike count (α) and width (σ). (D) Network firing with continuous noise current in the input layer. In the middle row (blue; all differentiator), the input layer firing rate is multiplied by 10 for clarity. (E) Analysis of signal transformations underlying stable propagation in the (σ, α) space. Each trajectory is formed by connecting (σ, α) of a propagating signal (dots) between adjacent layers, starting from the second layer output. Shade of each dot is the signal-to-noise ratio (S/N) and only points with S/N>1 are shown. Dotted circles mark “basins” where any propagating signal stays for ≥5 layers. A dotted line in the Middle panel is an approximated separatrix between trajectories toward a fixed point and dissipation. All models have 9 layers and the first 7 layers are shown in A-D for clarity (from Han et al., 2020).
Our study suggests that distinct cell types in neural circuits, performing different computational functions, facilitate information processing on the whole.
4. Publications
4.1 Journals
- E. De Schutter: Comment on “The growth of cognition: Free energy minimization and the embryogenesis of cortical computation". Physics of Life Reviews 36:1-2 (2020).
- D. Han, E. De Schutter and S. Hong: Lamina-specific neuronal properties promote robust, stable signal propagation in feedforward networks. Advances in Neural Information Processing Systems 33 (NeurIPS 2020)1828 (2020).
- Y. Zang, S. Hong and E. De Schutter: Firing rate-dependent phase responses of Purkinje cells support transient oscillations. eLife 9: 60692 (2020).
- I. Wichert, S. Jee, E. De Schutter, S. Hong: Pycabnn: Efficient and extensible software to construct an anatomical basis for a physiologically realistic neural network model. Frontiers in Neuroinformatics 14: 31 (2020).
- Y. Zang and E. De Schutter: The Cellular Electrophysiological Properties Underlying Multiplexed Coding in Purkinje Cells. Journal of Neuroscience 41: 1850-1863 (2021).
- S. Lindeman, S. Hong, L. Kros, J.F. Meijas, V. Romano, R. Oostenveld, M. Negrello, L.W.J Bosman, and C.I. De Zeeuw: Cerebellar Purkinje cells can differentially modulate coherence between sensory and motor cortex depending on region and behavior. Proceedings of the National Academy of Sciences USA 118: e2015292118 (2021).
4.2 Books and other one-time publications
Nothing to report.
4.3 Oral and Poster Presentations
- M. Kato, E. De Schutter, Simulating cell to cell interactions during the cerebellar development, CNS*2020 abstract P39 (2020, Online).
- A. Denizot, C. Cali, W. Chen, I. Hepburn, H. Berry, E. De Schutter, Reaction-diffusion simulations of astrocytic Ca2+ signals in realistic geometries, CNS*2020 abstract P41 (2020, Online).
- G. Capo Rangel, E. De Schutter, Responses of a Purkinje cell model to inhibition and excitation, CNS*2020 abstract P43 (2020, Online).
- A. Martyushev and E. De Schutter, 3D modeling of Purkinje cell activity, CNS*2020 abstract P44 (2020, Online).
- A. Markanday, S. Hong, J. Inoue, P. Dicke, E. De Schutter, P. Thier, Computational modeling of the input/output mapping in the cerebellar cortex, CNS*2020 abstract P200 (2020, Online).
- A. Denizot, C. Cali, H. Berry, E. De Schutter, Effect of the geometry of the endoplasmic reticulum on astrocytic Ca2+ signals at tripartite synapses: insights from simulations in realistic 3D geometries, SfN Global Connectome: A Virtual Event., January 11-13 2021.
- A. Denizot, C. Cali, H. Berry, E. De Schutter, Elucidating the morphology of the endoplasmic reticulum in fine astrocyte branchlets and its effect on calcium signals. Virtual Glia Trainee Symposium, March 11-13 2021.
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 OIST Computational Neuroscience Course 2020: Cancelled
- Date: June 29- July 16, 2020
- Venue: OIST Seaside House
- Organizers: Erik De Schutter (OIST), Kenji Doya (OIST), Bernd Kuhn (OIST), and Tomoki Fukai(OIST)
7. Other
Nothing to report.



