FY2022

Computational Neuroscience Unit
Professor Erik De Schutter

Abstract

We use computational, data-driven methods to study how neurons and microcircuits in the brain operate. We are interested  in how fundamental properties, such as a neuron’s nanoscale morphology and its excitability, interact with one another during common neural functions like information processing or learning. Most of our models concern the cerebellum as this brain structure has a relatively simple anatomy and the physiology of its main neurons has been studied extensively, allowing for detailed modeling at many different levels of complexity. More recently we have also built models of hippocampal synapses.

1. Staff

• Molecular modeling
  • Ryo Nakatani, PhD Student (from September 2022)
  • Sarah Yukie Nagasawa, PhD Student
• Cellular modeling
  • Sungho Hong, Group Leader
  • Alexey Martyushev, Postdoctoral scholar (till March 2023)
  • Gabriela Capo Rangel, Postdoctoral scholar
  • Audrey Denizot, JSPS Research Fellow (till December 2022)
• Network modeling
  • Mizuki Kato, PhD Student (till August 2022)
• Software development
  • Weiliang Chen, Staff Scientist
  • Iain Hepburn, Technical Staff
  • Jules Lallouette, Postdoctoral scholar
• Visiting Researcher
  • Andrew Gallimore, KAKENHI co-PI
  • Sergio Verduzco
  • Christos Kotsalos, EPFL
  • Tristan Carel, EPFL
  • Kerstin Lenk, TU Graz, Austria
• Visiting Research Student
  • Taro Yasuhi,Yamaguchi University School of Medicine
  • Domas Linkevicius, Edinburgh University
• Rotation Students
  • Tjon Saffira Yan
  • Juliana Silva de Deus
  • Rui Fukushima
• Research Interns
  • Quang Truong Duy Dang
  • Tim Kreuzer
  • Mohamed Rashed
• Research Unit Administrator
  • Chie Narai

2. Collaborations

• Theme: Spiking activity of monkey cerebellar neurons
  • Type of collaboration: Scientific collaboration
  • Researchers:
    • Professor H.P. Thier, University of Tübingen, Germany
    • Akshay Markanday, University of Tübingen, Germany
    • Junya Inoue, University of Tübingen, Germany
       
• Theme: Human Brain Project: simulator development
  • Type of collaboration: Scientific collaboration
  • Researchers:
    • Prof. F. Schürmann, École Polytechnique Fédérale de Lausanne, Switzerland
    • Dr. T. Carel, École Polytechnique Fédérale de Lausanne, Switzerland
    • Dr. G. Castiglioni, École Polytechnique Fédérale de Lausanne, Switzerland
    • Dr. A. Cattabiani, École Polytechnique Fédérale de Lausanne, Switzerland
       
• Theme: Quantitative molecular identification of hippocampal synapses
  • Type of collaboration: Scientific collaboration 
  • Researchers:
    • Prof. Dr. Silvio O. Rizzoli, Medical University Göttingen, Germany
       
• Theme: Cerebellar anatomy and physiology
  • Type of collaboration: Scientific collaboration
  • Researchers:
    • Professor C. De Zeeuw, Erasmus Medical Center, Rotterdam, The Netherlands
    • Professor L.W.J. Bosman, Erasmus Medical Center, Rotterdam, The Netherlands
    • Dr. M. Negrello, Erasmus Medical Center, Rotterdam, The Netherlands
       
• Theme: Purkinje cell morphology and physiology, modeling
  • Type of collaboration: Scientific collaboration
  • Researchers:
    • Professor M. Häusser, University College London, United Kingdom
    • Professor A. Roth, University College London, United Kingdom
    • Dr. S. Dieudonné, Ecole Normale Supérieure, Paris, France
    • Taro Yasuhi,Yamaguchi University School of Medicine

• Theme: Circadadian rhythm generation
  • Type of collaboration: Scientific collaboration
  • Researchers:
    • Professor J. Myung, Taipei Medical University, Taiwan

3. Activities and Findings

3.1 Software Development

STEPS 4.0: Fast and memory-efficient molecular simulations of neurons at the nanoscale

Recent advances in computational neuroscience have demonstrated the usefulness and importance of stochastic, spatial reaction-diffusion simulations. However, ever increasing model complexity renders traditional serial solvers, as well as naive parallel implementations, inadequate. We recently released version 4.0 of the  STochastic Engine for Pathway Simulation (STEPS) project (Chen, Carel et al., 2022).

Its core components have been designed for improved scalability, performance, and memory efficiency. STEPS 4.0 aims to enable novel scientific studies of macroscopic systems such as whole cells (see 3.3) while capturing their nanoscale details. This class of models is out of reach for serial solvers due to the vast quantity of computation in such detailed models, and also out of reach for naive parallel solvers due to the large memory footprint.

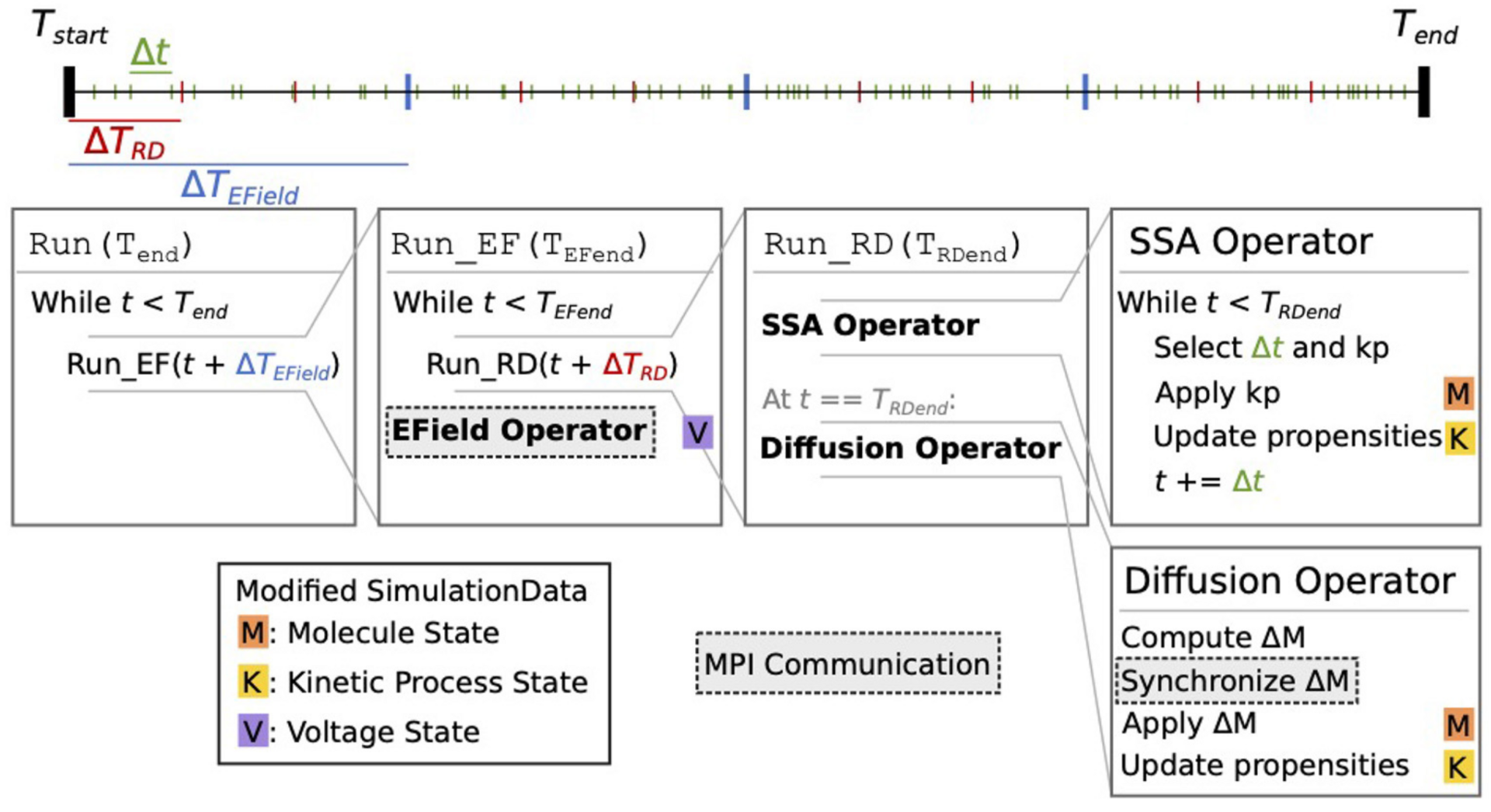
Figure 1: Schematic representation of the STEPS 4 simulation core loop. It shows nested loops running, respectively, EField Operator for membrane potential calculation at fixed T_Efield time steps and SSA Operator implementing the well-mixed Gillespie method followed by a Diffusion Operator (from Chen, Carel et al., 2022).

Based on a distributed mesh solution, we introduced a new parallel stochastic reaction-diffusion solver and a deterministic membrane potential solver in STEPS 4.0 (Figure 1). The distributed mesh, together with improved data layout and algorithm designs, significantly reduced the memory footprint of parallel simulations in STEPS 4.0. This enables massively parallel simulations on modern HPC clusters and overcomes the limitations of the previous parallel STEPS 3 implementation.  We benchmarked performance improvement and memory footprint on three published models with different complexities, from a simple spatial stochastic reaction-diffusion model, to a more complex one that is coupled to a deterministic membrane potential solver to simulate the calcium burst activity of a Purkinje neuron. Simulation results of these models suggest that the new solution dramatically reduces the per-core memory consumption by more than a factor of 30, while maintaining similar or better performance and scalability (Figure 2).

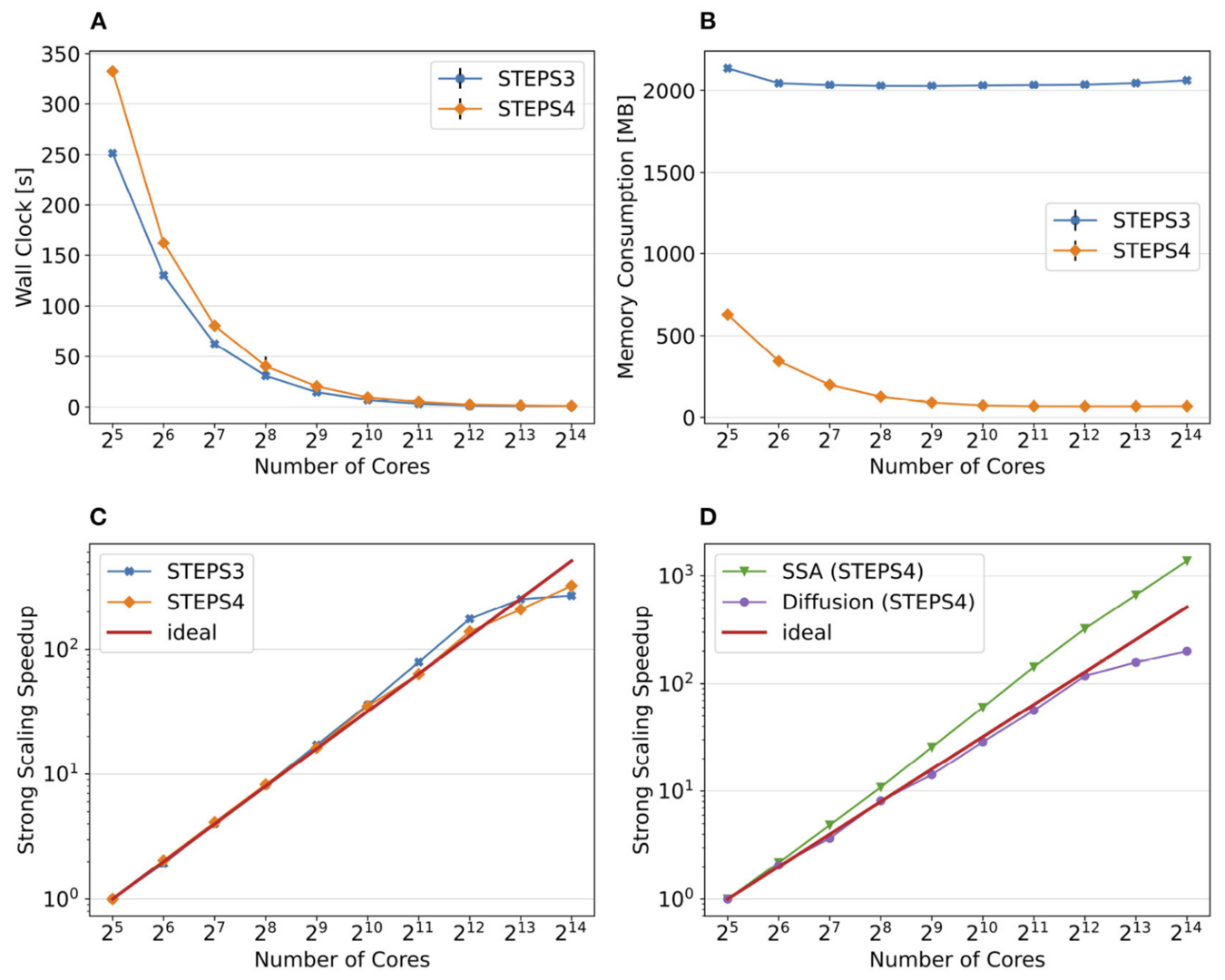
Figure 2: Comparison of performance and memory use of STEPS 4 to the previous STEPS 3 version for the calcium burst model. (A) Steady decrease of simulation time cost can be observed in both STEPS 4 and STEPS 3 simulations. (B) The memory footprint of STEPS 4 is superior compared to the STEPS 3 counterparts which consumes more than 2GB of memory per core for the whole series. (C) Both STEPS 4 and STEPS 3 demonstrate linear to super-linear scaling speedup. (D) Component scalability analysis of STEPS 4 suggests that the diffusion operator in STEPS 4 exhibits linear speedup until 1024 cores, while the SSA operator shows a remarkable super-linear speedup throughout the series (from Chen, Carel et al., 2022).

3.2 Modeling astrocytes

Control of calcium signals by astrocyte nanoscale morphology

Much of the Ca²⁺ activity in astrocytes is spatially restricted to microdomains and occurs in fine processes that form a complex anatomical meshwork, the so-called spongiform domain. A growing body of literature indicates that those astrocytic Ca²⁺ signals can influence the activity of neuronal synapses and thus tune the flow of information through neuronal circuits. Because of technical difficulties in accessing the small spatial scale involved, the role of astrocyte morphology on Ca²⁺ microdomain activity remains poorly understood. We used computational tools and idealized 3D geometries of fine processes based on recent super-resolution microscopy data to investigate the mechanistic link between astrocytic nanoscale morphology and local Ca²⁺ activity.

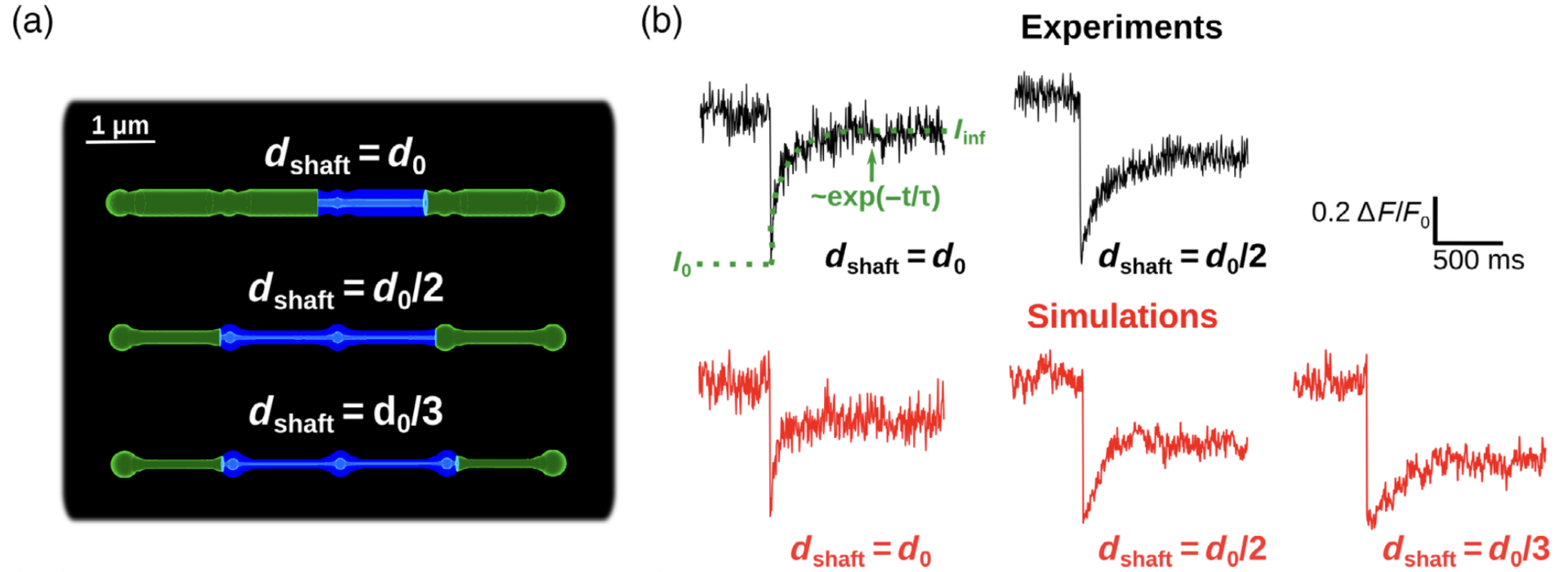
Figure 3: Simulations confirm that thin shafts favor node compartmentalization. (a) Geometries of different shaft widths used in the bleaching simulations. Blue color represents the bleached volume, which varied depending on the value of dshaft in order to fit experimental values. (b) Representative experimental (top, from Arizono et al. Nat. Comm. 2020) and simulation (bottom) traces for different shaft width values (from Denizot et al. 2022).

We test whether the geometries used are a good approximation of the ultrastructure of the gliapil by comparing molecular diffusion flux in those geometries with those reported experimentally. To do so, we simulated photobleaching experiments (Figure 3) and found a good match to the data. Simulations demonstrate that the nano-morphology of astrocytic processes powerfully shapes the spatio-temporal properties of Ca²⁺ signals generated by IP₃ mediated release from the endoplasmic reticulum. Small diameter shafts promote  local Ca²⁺ activity and these stronger signals then spread to neighboring nodes (Figure 4).

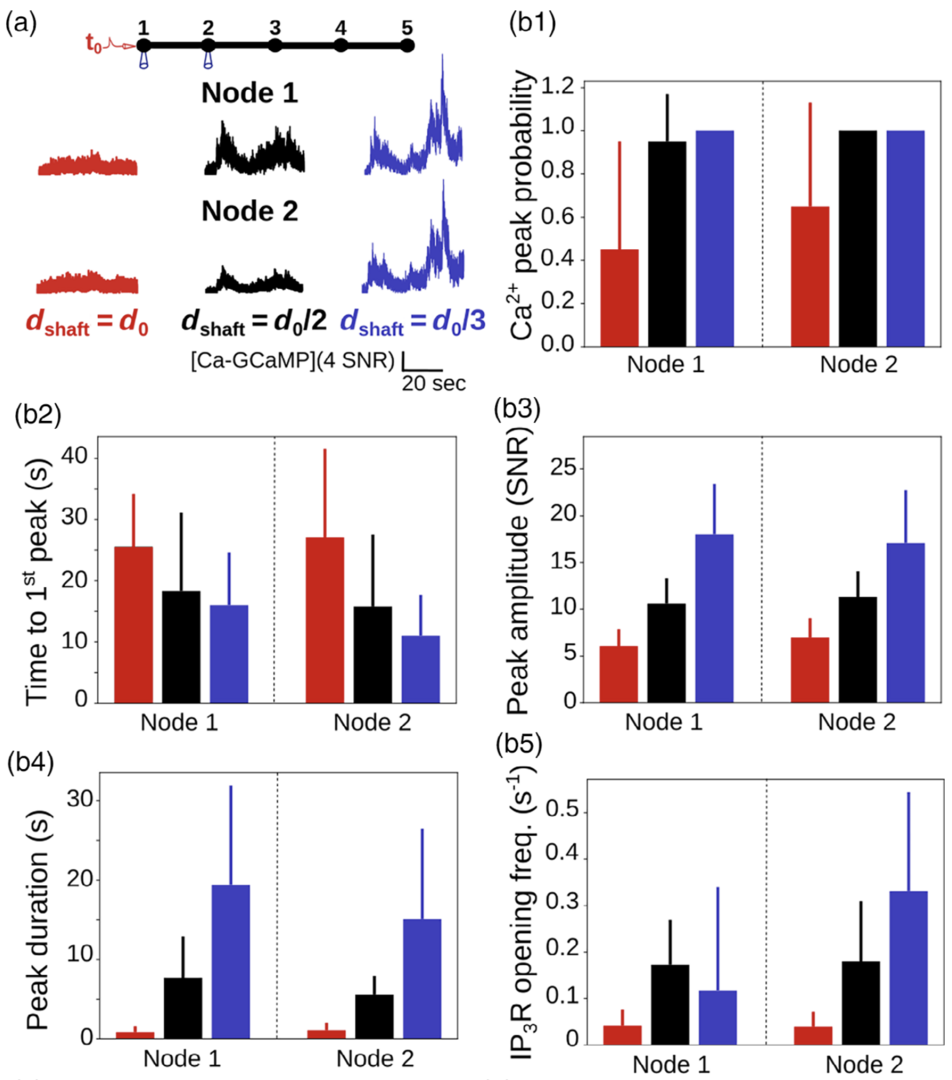
Figure 4: Ca²⁺ peak probability, amplitude and duration increase when shaft width decreases. (a) (top) Neuronal stimulation protocol simulated for each geometry: Node 1 was stimulated  while Ca²⁺ activity was
monitored in node 2. (bottom) Representative Ca²⁺ traces for different shaft widths. (b) Quantification of the effect of dshaft on Ca²⁺ signal characteristics data are represented as mean ± STD, n = 20. Ca²⁺peak probability increases (***, b1), time to 1st peak decreases (***, b2), peak amplitude (***, b3) and duration (***, b4) increase when dshaft decreases (from Denizot et al. 2022). 

The model predicts therefore that upon astrocytic swelling, hallmark of brain diseases,  astrocytic signal propagation will be reduced (Figure 5).  Overall, this study highlights the influence of the complex morphology of astrocytes at the nanoscale and its remodeling in pathological conditions on neuron-astrocyte communication at so-called tripartite synapses, where astrocytic processes come into close contact with pre- and postsynaptic structures.

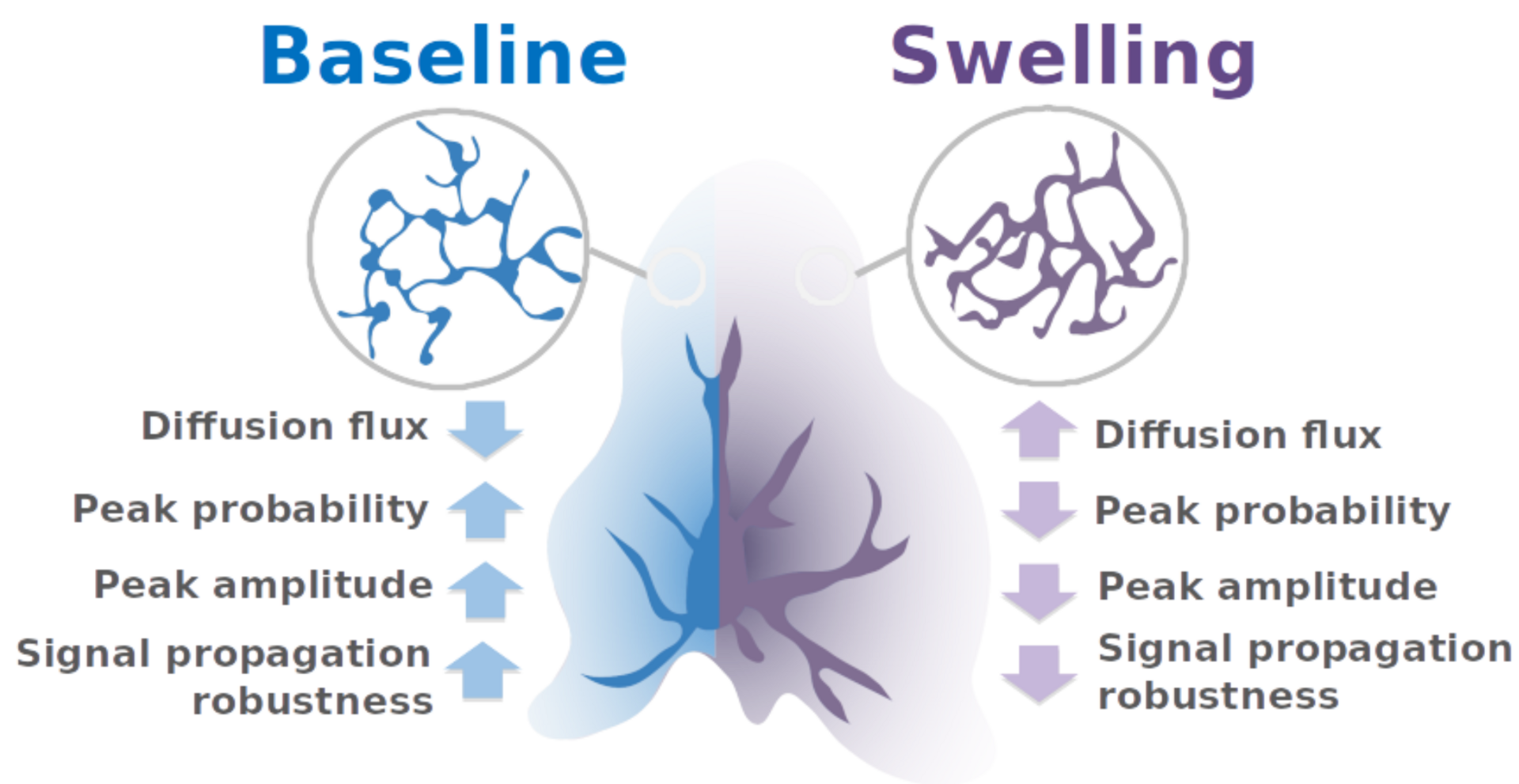
Figure 5: summary of the pathological effect of astrocytic swelling on signal propagation with astrocytes.

3.3 Single cell modeling

Modeling Neurons in 3D at the Nanoscale

For decades, neurons have been modeled by methods developed by early pioneers in the field such as Rall, Hodgkin and Huxley, as cable-like morphological structures with voltage changes that are governed by a series of ordinary differential equations describing the conductances of ion channels embedded in the membrane. In recent years, advances in experimental techniques have improved our knowledge of the morphological and molecular makeup of neurons, and this has come alongside ever-increasing computational power and the wider availability of computer hardware to researchers. This has opened up the possibility of more detailed 3D modeling of neuronal morphologies and their molecular makeup at the nanoscale, a new, emerging component of the field of computational neuroscience.
Many scientists may be familiar with 1D models yet unfamiliar with the more detailed 3D description of neurons. In Chen, Hepburn et al. (2022) the steps required for building such models from a foundation of the more familiar 1D description are described. They fall broadly into two categories: morphology and how to build a 3D computational mesh based on a cable-like description of the neuronal geometry or directly from imaging studies, and biochemically how to define a discrete, stochastic description of the molecular neuronal makeup. This was demonstrated this with a full Purkinje cell model, implemented in 3D simulation in STEPS 3.6 (Figure 6).

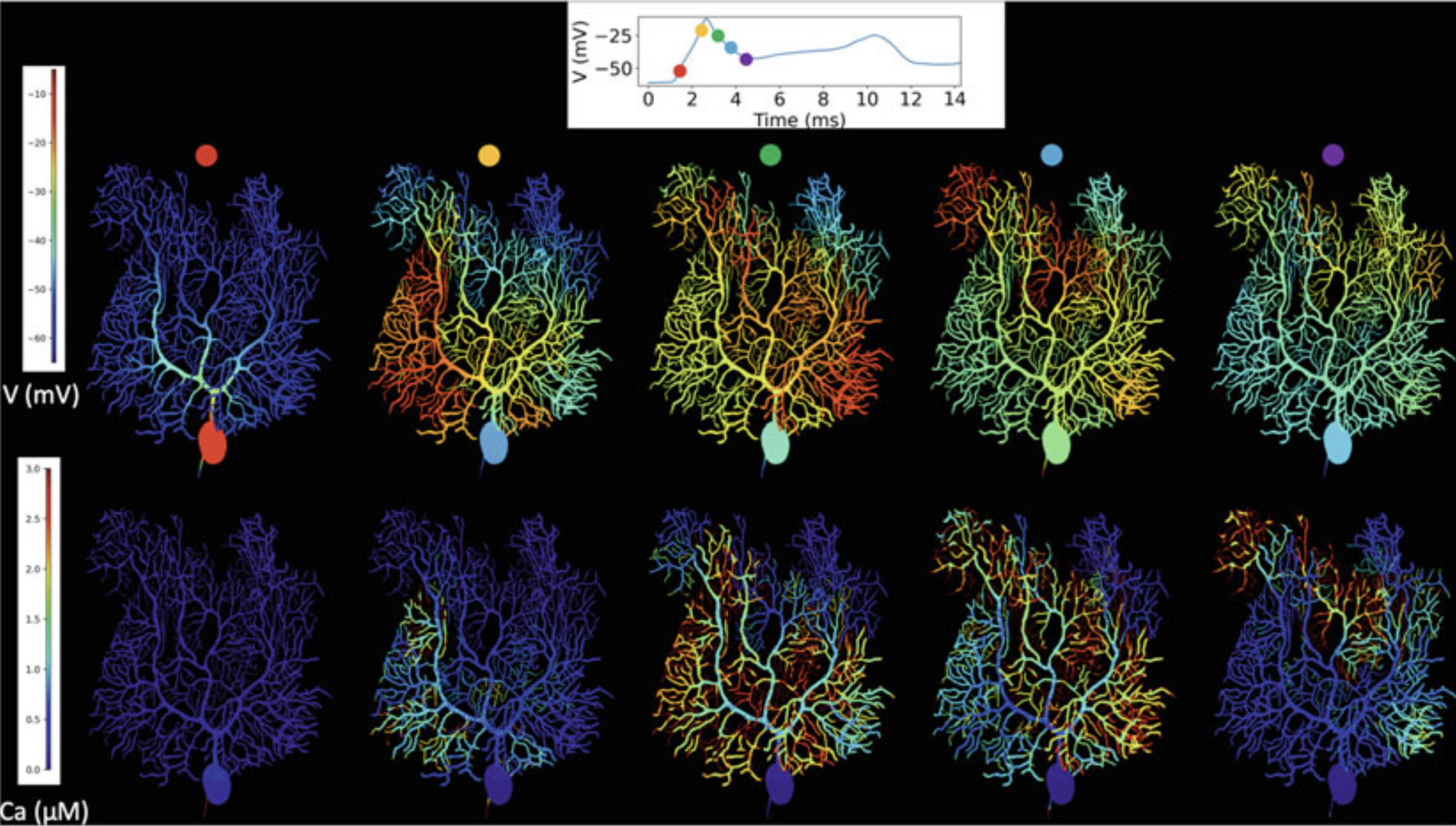
Figure 6: Complex spike simulation in a STEPSmodel of the Purkinje cell during the first dendritic spike. Top: membrane potential, full voltage trajectory in the smooth dendrite shown in inset. Bottom: calcium concentrations in a constant volume under each surface triangle. For calcium concentrations a truncated color scale was used to highlight lower concentrations, maximum dendritic con-centration was approximately 10 μM, truncated at 3 μM. Simulation was run on 160 cores with a run-time of 5.5 h, using STEPS 3.6 without core splitting (from Chen, Hepburn et al., 2022).

3.4 Motor control modeling

A differential Hebbian framework for biologically-plausible motor control

Verduzco-Flores et al. (2022) explore a neural control architecture that is both biologically plausible, and capable of fully autonomous learning. It consists of feedback controllers that learn to achieve a desired state by selecting the errors that should drive them. This selection happens through a family of differential Hebbian learning rules that, through interaction with the environment, can learn to control systems where the error responds monotonically to the control signal (Figure 7).

In a more general case, neural reinforcement learning can be coupled with a feedback controller to reduce errors that arise non-monotonically from the control signal. The use of feedback control can reduce the complexity of the reinforcement learning problem, because only a desired value must be learned, with the controller handling the details of how it is reached.This makes the function to be learned simpler, potentially allowing learning of more complex actions. Verduzco-Flores et al. (2022) uses the inverted pendulum problem to illustrate the approach. Figure 8 shows how it could be extended to hierarchical architectures.

Self-configuring feedback loops for sensorimotor control

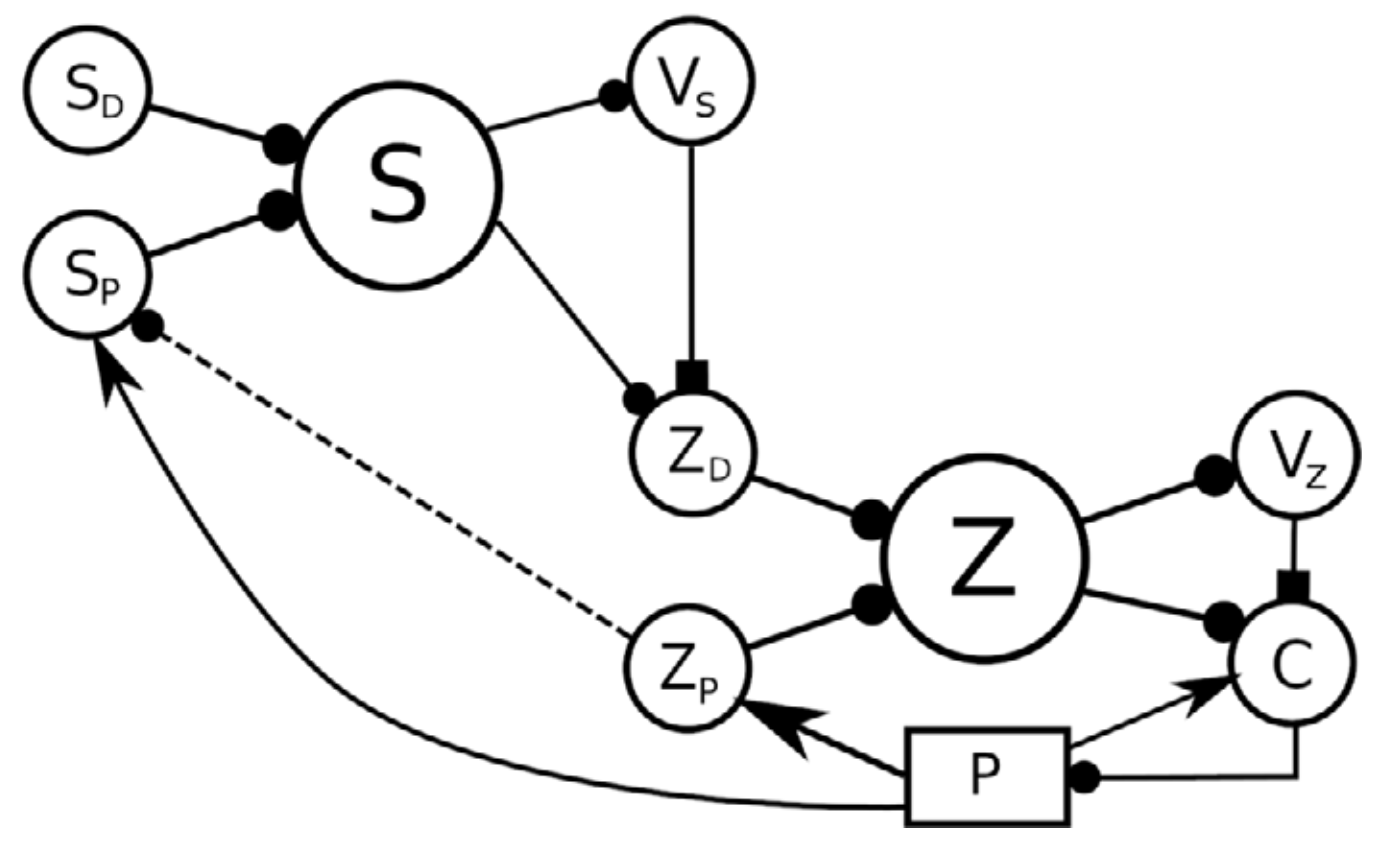
How dynamic interactions between nervous system regions in mammals performs online motor control remains an unsolved problem. Verduzco Flores and De Schutter (2022) show that feedback control is a simple, yet powerful way to understand the neural dynamics of sensorimotor control. We used a minimal model comprising spinal cord, sensory and motor cortex, coupled by long connections that are plastic (Figure 9).

Figure 9: Main components of the model of Verduzco-Flores and De Schutter, 2022. In the left panel, each box stands for a neural population, except for P, which represents the arm and the muscles. Arrows indicate static connections, open circles show input correlation synapses, and the two colored circles show possible locations of synapses with the learning rule in Verduzco-Flores et al., 2022. In the static network all connections are static. A : afferent population. SA : Somatosensory cortex, modulated by afferent input. SP : somatosensory cortex, prescribed pattern. SPA : population signaling the difference between SP and SA. M : primary motor cortex. C : spinal cord. Inside the C box the circles represent the excitatory (CE) and inhibitory (CI) interneurons, organized into six pairs. The interneurons in each pair innervate an alpha motoneuron (α), each of which stimulates one of the six muscles in the arm, numbered from 0 to 5. The trios consisting of CE, CI, α units are organized into agonists and antagonists, depending on whether their α motoneurons cause torques in similar or opposite directions. These relations are shown in the right-side panel.

It succeeds in learning how to perform reaching movements of a planar arm with 6 muscles in several directions from scratch after a few reaches (Figure 10). The model satisfies biological plausibility constraints, like neural implementation, transmission delays, local synaptic learning and continuous online learning. Using differential Hebbian plasticity the model can go from motor babbling to reaching arbitrary targets in less than 10 min of in silico time.

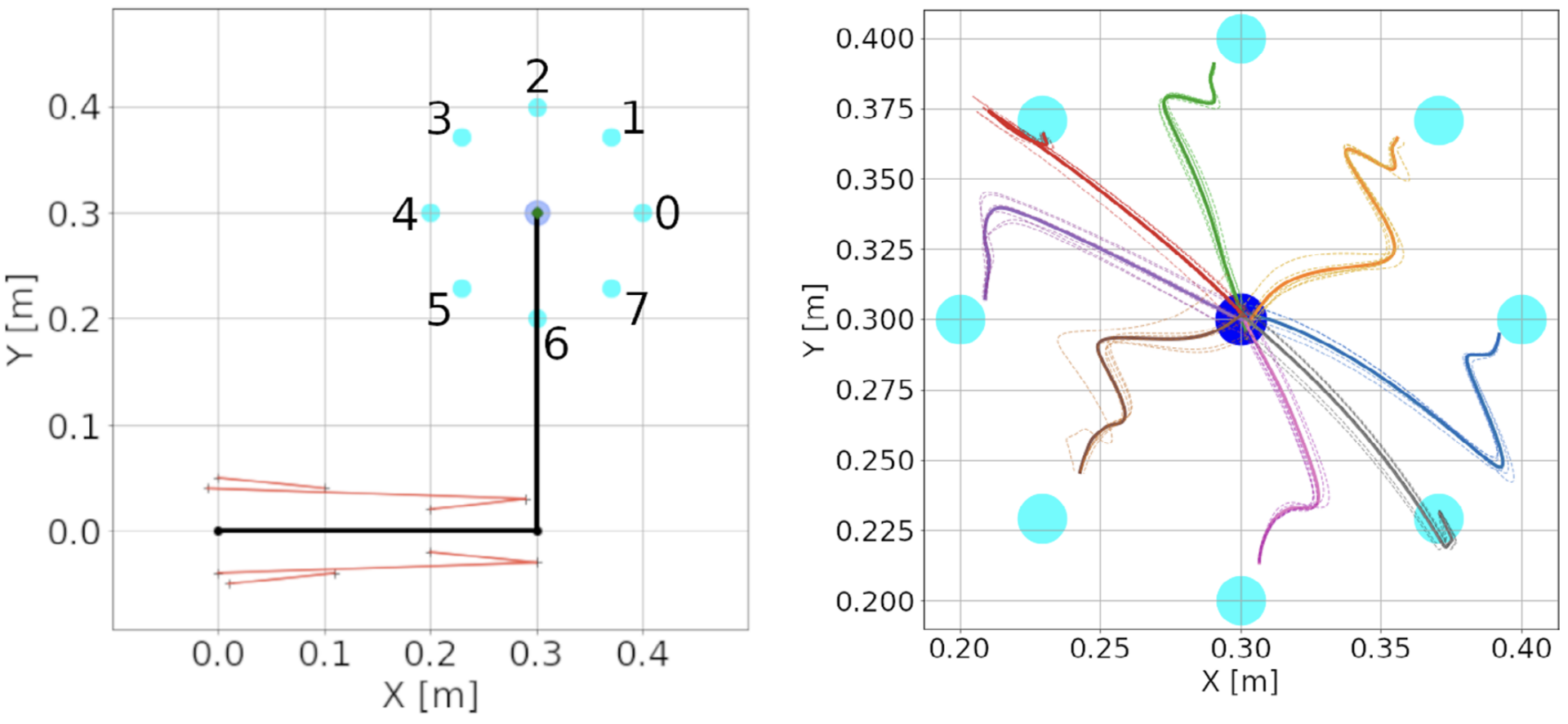Figure 10: Center-out reaching. (A) The arm at its resting position, with hand coordinates (0.3, 0.3) meters, where a center target is located. Eight peripheral targets (cyan dots) were located on a circle around the center target, with a 10 cm radius. The muscle lines, connecting the muscle insertion points, are shown in red. The shoulder is at the origin, whereas the elbow has coordinates (0.3, 0). Shoulder insertion points remain fixed. (B) Hand trajectories for all reaches in the spinal learning configuration. The trajectory’s color indicates the target. Dotted lines show individual reaches, whereas thick lines indicate the average of the 6 reaches. While the arm successfully reaches the targets, it's final movements are ataxic (from Verduzco-Flores and De Schutter, 2022).

Moreover, independently of the learning mechanism, properly configured feedback control has many emergent properties: neural populations in motor cortex show directional tuning (Figure 11) and oscillatory dynamics, the spinal cord creates convergent force fields that add linearly, and movements are ataxic (as in a motor system without a cerebellum).

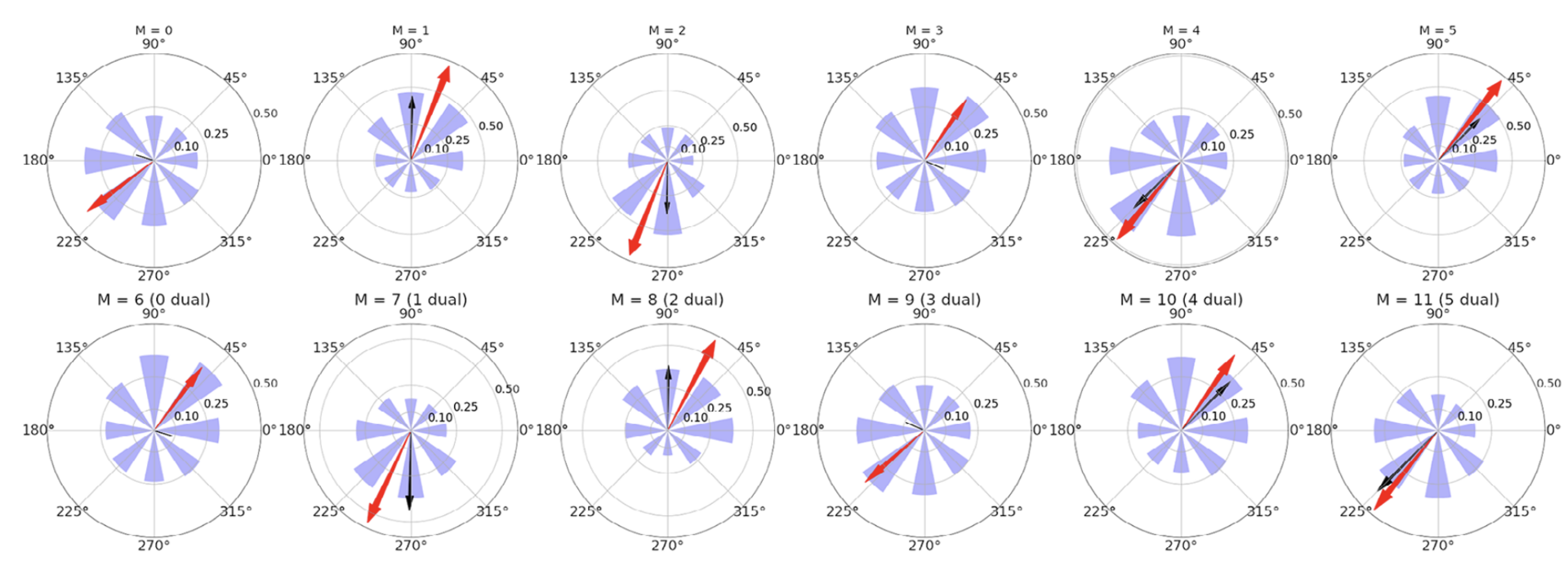
Figure 11: Directional tuning of the units in motor cortex (M) for a simulation with the spinal learning model. Average firing rate per target, and preferred direction for each of the 12 units in M. Each polar plot corresponds to a single unit, and each of the 8 purple wedges corresponds to one of the 8 targets. The length of a wedge indicates the mean firing rate when the hand was reaching the corresponding target. The red arrow indicates the direction and relative magnitude of the preferred direction vector. The black arrow shows the predicted preferred direction vector (from Verduzco-Flores and De Schutter, 2022).

4. Publications

4.1 Journals

1. S. Verduzco-Flores and E. De Schutter​: Self-configuring feedback loops for sensorimotor control. eLife: 77216.
2. A. Denizot, M. Arizono, V.U. Nägerl, H. Berry and Erik De Schutter: Control of Ca²⁺ signals by astrocyte nanoscale morphology at tripartite synapses. Glia 70: 2378-2391.
3. W. Chen, I. Hepburn, A. Martyushev and E. De Schutter: Modeling Neurons in 3D at the Nanoscale. In: Giugliano, M., Negrello, M., Linaro, D. (eds) Computational Modelling of the Brain. Advances in Experimental Medicine and Biology 1359: 3-24. Springer, Cham.
4. W. Chen, T. Carel, O. Awile, N. Cantarutti, G. Castiglioni, A. Cattabiani, B. Del Marmol, I. Hepburn, J.G. King, C. Kotsalos, P. Kumbhar, J. Lallouette, S. Melchior, F Schürmann and E. De Schutter: STEPS 4.0: Fast and memory-efficient molecular simulations of neurons at the nanoscale. Frontiers in Neuroinformatics 16: 883742.
5. S. Verduzco-Flores, W. Dorrell and E. De Schutter: A differential Hebbian framework for biologically-plausible motor control. Neural Networks 150: 237–258.
6. A. Covelo , A. Badoual and A. Denizot: Reinforcing Interdisciplinary Collaborations To Unravel The Astrocyte "Calcium Code". Journal of Molecular Neuroscience 72: 1443–1455.
7. L. Medlock, K. Sekiguchi, S. Hong, S. Dura-Bernal, W. Lytton and S. Prescott: Multiscale computer model of the spinal dorsal horn reveals changes in network processing associated with chronic pain. Journal of Neuroscience 42: 3133-3149.

4.2 Preprints

1. M. Kato and E. De Schutter: Models of Purkinje cell dendritic tree selection during early cerebellar development. Preprint at https://www.biorxiv.org/content/10.1101/2022.10.18.512799v1.
2. E. De Schutter: Efficient simulation of neural development using shared memory parallelization. Preprint at https://www.biorxiv.org/content/10.1101/2022.10.17.512465v1.
3. A. Denizot, M.F. Veloz Castillo, P. Puchenkov, C. Calì and E. De Schutter: The endoplasmic reticulum in perisynaptic astrocytic processes: shape, distribution and effect on calcium activity.
   Preprint at https://www.biorxiv.org/content/10.1101/2022.02.28.482292v1.
4. A. Markanday*, S. Hong*, J. Inoue, E. De Schutter and P. Thier: Multidimensional cerebellar computations for flexible kinematic control of movements.
   Preprint at https://www.biorxiv.org/content/10.1101/2022.01.11.475785v1.

4.3 Books and other one-time publications

Nothing to report

4.4 Oral and Poster Presentations

1. A.MARKANDAY, S. HONG, J. INOUE, E. DE SCHUTTER, P. THIER; Multidimensional cerebellar computations for flexible kinematic control of movements, Neuroscience 2022, Society for Neuroscience, November 2022. (Poster)
2. A. Denizot, M. F. Veloz Castillo, P. Puchenkov, C. Cali, E. De Schutter. Ultrastructural and functional study of the endoplasmic reticulum in perisynaptic astrocytic processes, Neuroscience 2022, Society for Neuroscience, online, November 2022. (Poster)
3. E. De Schutter, Modeling the tripartite synapse at the nanoscale, 12th European Conference on Mathematical and Theoretical Biology, Heidelberg, Germany. September 19, 2022.
4. A. Martyushev, E. De SchutterNanoscale computational modeling explains why evolutionary shift happened, NEURO2022, Okinawa, Japan, Fri. Jul 1, 2022. (Poster)
5. S. Yukie Nagasawa, I. Hepburn, A. R. Gallimore, E. De Schutter, Stochastic spatial modeling of vesicle-mediated trafficking of AMPA receptors for understanding hippocampal synaptic plasticity mechanisms, NEURO2022, Okinawa, Japan, Fri. Jul 1, 2022.(Poster)
6. A. Denizot, M. Fernanda Veloz Castillo, C. Calì, E. De Schutter, Endoplasmic reticulum-plasma membrane contact sites in perisynaptic astrocytic processes: properties and effects, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022.(Oral)
7. S. Hong, A. Markanday, J. Inoue, E. De Schutter, P. Thier, Multidimensional cerebellar computations for flexible kinematic control of movements, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022(Oral).
8. J. Lallouette, E. De Schutter, A novel python programming interface for STEPS, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022.(Poster)
9. W. Chen, T. Carel, I. Hepburn, J. Lallouette, A. Cattabiani, C. Kotsalos, N., P. Kumbhar, J. Gonzalo King, E. De Schutter, The STEPS distributed solver: Optimizing memory consumption of large scale spatial reaction-diffusion parallel simulations, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022.(Poster)
10. M. Kato, E. De Schutter, A computational model for dendritic pruning in the cerebellum induced by intercellular interactions, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022.(Poster).
11. I. Hepburn, W. Chen, J. Lallouette, A. Gallimore, S. Yukie Nagasawa, E. DeSchutter, Parallel modeling of vesicles in STEPS, NEURO2022, Okinawa, Japan, Sat. Jul 2, 2022.(Poster)
12. A. Denizot, M. F. Veloz Castillo, P. Puchenkov, C. Cali, E. De Schutter. The endoplasmicreticulum in fine astrocytic processes: presence, shape, distribution and effect on Ca2+ activity, Federation of European Neuroscience Societies Forum 2022, Paris, France, July 2022. (Poster)
13. G. CapoRangel, Understanding brach-specific parallel fiber computation in a Purkinje cell through a heterogenous ion channel density model, Dendrites 2022, EMBO Workshop Dendritic anatomy, molecules and function, Heraklion, 23-26 May, 2022.(Oral)

4.5 Invited talks

1. Title: Modeling the tripartite synapse.
   Invitation: Quantitative Synaptology talk, Universitäts medizin Göttingen, Germany.
   Date: September 2, 2022.
   Speaker: Erik De Schutter (remote).

2. Title: Modeling the tripartite synapse at the nanoscale.
   Invitation (symposium): 12th European Conference on Mathematical and Theoretical Biology, Heidelberg, Germany.
   Date: September 19, 2022.
   Speaker: Erik De Schutter.

3. Title: Multidimensional cerebellar computations for flexible kinematic control of movements.
   Invitation: Dr. Paul Chadderton, School of Physiology, Pharmacology & Neuroscience, University of Bristol, Bristol, UK.
   Date: June 13, 2022.
   Speaker: Hong Sungho (Group Leader).

4. Title: Neural geometry and dynamics of cerebellar computations.
   Invitation: Dr. Jihwan Myung, Graduate Institute of Mind, Brain and Consciousness, Taipei Medical University, Taipei, Taiwan (remote).
   Date: December 16, 2022.
   Speaker: Hong Sungho (Group Leader).

5. Intellectual Property Rights and Other Specific Achievements

Nothing to report

6. Meetings and Events

6.1 OCNC: OIST Computational Neuroscience Course 2022

• Dates: June 13-29 (arrival June 12, departure June 30)
• Venue: OIST Seaside House
• Co-organizers: Kenji Doya (OIST), Tomoki Fukai (OIST), and Bernd Kuhn (OIST)
• Sponsers: SECOM Science and Technology Foundation, JapanDr. First Last (Affiliation)

7. Other

Nothing to report.