[Seminar] Classification of classical spin liquid in the large-S limit

Speaker

Dr. Han Yan - Rice University
HY’s reserach interest is in frustrage magnets and spin liquids, as well as intersections between high-energy theory and condensed matter theory.
He is currently a Junior Fellow at Rice Academy of Fellows, Rice University, and is supervised by Prof. Andriy Nevidomskyy in the Department of Physics and Astronomy.
Before joining Rice, HY obtained his Ph.D. from OIST, under supervison of Prof. Nic Shannon in the TQM Unit (co-supervised by Prof. Hirotaka Sugawara). He is the receipient of the Peter Gruss Doctoral Dissertation Excellence Award (2021), the Award for Student Excellence in Graduate Research (inaugural awardee, 2019), and the JSPS DC2 Fellowship (2018 - 2020).

Title

Classification of classical spin liquid in the large-S limit

Abstract

Classical spin liquids are arguably one of the most interesting types of classical matter. They are described often by the classical limit of gauge theories (electrostatics), and can be upgraded to topological orders or gapless quantum liquid states if equipped with proper quantum dynamics.
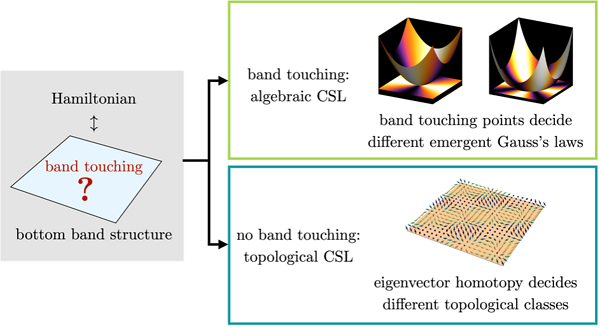
In this work, we present a classification scheme for classical spin liquids in the large-S limit. In this limit, the spin components are effectively real scalars, so the spectrum of the Hamiltonian accurately describes their properties. We found that the ground state degeneracy corresponds to flat bands at the bottom of the spectrum, and it crucially decides the physics of the classical spin liquid. When there is a singular band-touching between the top bands and the bottom ones, the system has algebraic correlaion. The ground state is then described by a generalized Gauss’s law, whose algebraic form is determined by the band touching structure. A much less studied category is when the flat bands are gapped from the top ones. In this case, the correlation is short-ranged, but the classical spin liquid can be distinguished from a trivial paramagnet by the fragile topological homotopy of the bottom bands. Besides building the general mathematical framework of the classification, I will also show some concrete examples and discuss experimental applications.

Join Zoom Meeting

Meeting ID: 920 8887 3379