FY2019 Annual Report
Theory of Quantum Matter Unit
Professor Nic Shannon
Abstract
FY2019 was an unusual, but none the less productive, year for OIST's Theory of Quantum Matter (TQM) Unit. The year began with Prof. Shannon on Sabbatical in Munich, and ended with all travel and scientific events being cancelled as result of the COVID-19 pandemic.
The TQM Unit welcomed a new PhD student, Ms Leilee Chojnacki, and celebrated Dr Judit Romhanyi moving on to a faculty position at the University of California, Irvine. Meanwhile Han Yan successfully defended his PhD Thesis, and was awarded OIST's inaugural Award for Student Excellence in Graduate Research. The Unit was also part of a succesful bid for a Grant-in-Aid for Scientific Research on Innovative Areas titled “Quantum Liquid Crystals” (KAKENHI Grant No. JP19H05825). And the former Unit member, Dr Olga Sikora, succesfully defended her Habilitation Thesis in Poland, based on work carried out in the TQM Unit.
The Unit published 10 papers in FY 2019, including one article in Proceedings of the National Academy of Science, three in Physical Review Letters (one of which was singled out as an Editor's suggestion and featured in Physics Magazine) and six in Physical Review B (one of which was also singled out as an Editor's suggestion). These covered a range of topics in the physics of quantum materials, and topological phases of matter.
Research highlights included the (probable) identification of quantum spin nematic phases in both volborthite and BaCdVO(PO4)2; the explanation of negative thermal expansion in CdCr2O4; the discovery of a "ripple" phase in honeycomb lattice antiferromagnets; further discoveries about the connections between fractons and holography; and the discovery of a route to fracton phases in real materials and an exploration of the properties of water ice in electric field. A significant new theme also emerged over the course of the year, namely use of Machine Learning as a tool for solving theoretical physics problems
The Unit remained active in promoting its work, giving a total of 30 presentations in FY2019, including 22 invited talks, among them seminars at MIT, Oxford, and Princeton. Many of the Unit also participated in the program "Topological Quantum Matter: Concepts and Realisations" at the Kavli Institute for Theoretical Physics (KITP,) in Santa Barbara, which was co-organised by Prof. Shannon. However two of the most significant conferences in which Unit members were due to participate, the APS March Meeting, and the JPS Spring Meeting, were cancelled as a result of the coronavirus.
The TQM Unit hosted a smaller number of visits and semianrs in FY 2019 than in previous years, both because of Prof. Shannon's sabbatical, and travel restrictions coming from the coronavirus. None the less 7 researchers did visit the Unit, giving 6 seminars. And at the end of FY2019, the TQM moved its seminar series online, by way of Zoom.
Outreach activity also took an interesting new turn: the TQM Unit was the subject of a film commissioned by the American Physical Society for its "APS TV", and a second film, profiling the Unit's former student Rico Pohle, was commissioned by OIST.
1. Staff
- Dr. Judit Romhanyi, Staff Scientist (~2019.08)
- Dr. Matthias Gohlke, Postdoctoral Scholar
- Dr. Geet Rakala, Postdoctoral Scholar
- Dr. Tokuro Shimokawa, Postdoctoral Scholar
- Ms. Leilee Chojnacki, PhD Student
- Mr. Soshi Mizutani, PhD Student
- Ms. Kimberly Remund, PhD Student
- Mr. Andreas Thomasen, PhD Student
- Mr. Han Yan, PhD Student
- Ms. Megumi Ikeda, Research Unit Administrator
2. Collaborations
2.1 Polarization plateaus in hexagonal water ice
- Type of collaboration: Joint research
- Researchers:
- Dr. Matthias Gohlke, OIST
- Prof. Roderich Moessner, MPI-PKS Dresden, Germany
- Prof. Frank Pollmann, TU Munich, Garching, Germany
2.2 Field-induced pseudo-Goldstone mode and nematic phase in the Kitaev-Gamma model
- Type of collaboration: Joint research
- Researchers:
- Dr. Matthias Gohlke, OIST
- Mr. LI Ern Chern, University of Toronto, Canada
- Prof. Yong Baek Kim, University of Toronto, Canada
2.3 Machine learning the spinnon dynamics
- Desctiption: we explore how modern machine learning (ML) methods can be used to extend the time dependent dependent correctors which are obtained by tDMRG algorithm for quantum spin chain system with spinnon dynamics, and the performance is compared to the Bethe ansatz solution and the existing linear prediction method. For this project, ML and tDMRG calculations are carried out by Mizutani while Bethe ansatz calcuation is carried out by Caux, under the supervision of Shannon, Pollmann and Caux.
- Type of collaboration: Joint research
- Researchers:
- Mr. Soshi Mizutani, OIST
- Prof. Nic Shannon, OIST
- Prof. Frank Pollmann, Technical Univeristy of Munich
- Prof. Jean-Sébastien Caux, Institute of Physics, University of Amsterdam
2.4 Machine learning the quench dynamics
- Description: We apply machine learning based forecasting methods to extend the quenching signal of bose gas density function computed by DMFT and tDMRG and its long time behavior.
For this project, ML implementation is carried out by Mizutani while DMFT and tDMRG calcuations are carried out by Grundner, under the supervision of Shannon and Schollwöck. - Type of collaboration: Joint research
- Researchers:
- Mr. Soshi Mizutani, OIST
- Prof. Nic Shannon, OIST
- Mr. Martin Grundner, Ludwig Maximilian University of Munich
- Prof. Ulrich Schollwöck, Ludwig Maximilian University of Munich
2.5 Investigating Magnetic Phases of Matter Using Autoregressive Neural Networks
- Description: This collaboration investigates changes of state in condensed matter physics research by training a neural network to produce and sample probability distributions of spin-configurations. The network is trained through free energy minimization using state-of-the-art machine learning technology.
- Type of collaboration: Joint research
- Researchers:
- Prof. Judit Romhanyi, University of California Irvine
- Prof. Nic Shannon, OIST
- Mr. Andreas Thomasen, OIST
2.6 Chaotic Few-Body Vortex Dynamics in Rotating Bose-Einstein Condensates
- Description: Chaotic phenomena in physics are ubiquitous and numerous examples exist in the natural world as soon as one goes beyond the classical two-body problem. These are interesting because while the equations of motion are known, the solutions are generally not known analytically, and their evolution is hard to predict.In this study we tracked the trajectories of 4 vortices in a Bose-Einstein condensate and identified chaotic behavior arising when one of the vortices had opposite winding as compared to the others. Chaotic behavior is generally observed most strongly when three or more vortices are in the vicinity of each other. These collisional events appear to be the main cause of chaotic behavior in Bose Einstein condensates we investigated.
- Type of collaboration: Joint research
- Researchers:
- Prof. Thomas Busch, OIST
- Dr. Angela White, OIST
- Dr. Lee O'Riordan, OIST
- Dr. James Schloss, OIST
- Mr. Tiantan Zhang, Norwegian University of Science and Technology
- Mr. Andreas Thomasen, OIST
2.7 Quantum dipolar spin ice in applied magnetic field
- Description: Quantum Monte Carlo simulations of a quantum dipolar spin ice in applied magnetic field.
- Type of collaboration: Joint research
- Researchers:
- Prof. Karlo Penc, Budapest
- Prof. Nic Shannon, OIST
- Prof. Frank Pollmann, TUM
- Dr. Olga Sikora, IFJ Krakow
2.8 Hard plates on a cubic lattice
- Type of collaboration: Joint research
- Researchers:
- Dr. Geet Rakala, OIST
- Prof. Kedar Damle, TIFR Mumbai, India
- Prof. Deepak Dhar, IISER, Pune, India
2.9 Triangular Ising antiferromagnet with further neighbour interactions
- Type of collaboration: Joint research
- Researchers:
- Dr. Geet Rakala, OIST
- Prof. Kedar Damle, TIFR Mumbai, India
2.10 Numerical simulation of spin-1 magnets
- Type of collaboration: Joint research
- Researchers:
- Ms. Kimberly Remund, OIST
- Dr. Rico Pohle. Waseda University
- Prof. Judit Romhanyi, University of California Irvine
- Prof. Yutaka Akagi, The University of Tokyo
- Prof. Nic Shannon, OIST
2.11 Generalized hyperbolic fracton model
- Description: We study the generalized classical fracton topological order and subsystem symmetry protected states in the hyperbolic space. We will explore the subsystem symmetries of these models, the boundary state representations, and their relation to holographic entanglement entropy.
- Type of collaboration: Joint research
- Researchers:
- Mr. Han Yan, OIST
- Dr. Dominic Joseph Williamson, Stanford Universty
- Dr. Zhu-Xi Luo, KITP, University of California, Santa Barbara
2.12 Machine learning complex order
- Type of collaboration: Joint research
- Researchers:
- Mr. Han Yan, OIST
- Dr Ludovic Jaubert, Bordeaux
- Mr Nicolas Sadoune, LMU
- Dr Wan Ke, LMU
- Prof. Lode Pollet, LMU
- Prof. Nic Shannon, OIST
2.13 Topological bands in quantum magnets
- Type of collaboration: Joint research
- Researchers:
- Mr. Andreas Thomasen, OIST
- Mr Han Yan, OIST
- Prof. Judit Romhanyi, UCI
- Prof. Karlo Penc, Budapest
- Prof. Nic Shannon, OIST
2.14 Imaging magnetic monopoles in spin ice
- Type of collaboration: Joint research
- Researchers:
- Mr. Ankur Dahr, OIST
- Dr Ludovic Jaubert, CNRS Bordeaux
- Prof. Nic Shannon, OIST
- Prof. Tsumoru Shintake, OIST
3. Activities and Findings
1. Theory of exotic spin liquid sheds light on entanglement structure of quantum gravity.
The holographic principle has played a central role in the modern study of quantum gravity. It states that gravitational theory in a negatively curved spacetime is equivalent to a conformal quantum field theory on its boundary. Many toy models have been built to help us understand holography more intuitively, including the perfect tensor-networks, the bit-threads model, and more recently the fracton model proposed by the author.
In this work, the author proposed that all three types of toy models can be unified under the same picture: geodesic string condensation. Furthermore, a rank-2 U(1) gauge theory, previously discussed in the constex of "fractons", and as a theory of exotic spin liquids, can also be considered as a linearized limit of gravity, and displays holographic properties when embedded in a curved space-time. This work illuminates the how the holographic toy models are connected with gravity concretely.
This work was published as: "Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Han Yan, Phys. Rev. B 102, 161119(R) (2020).
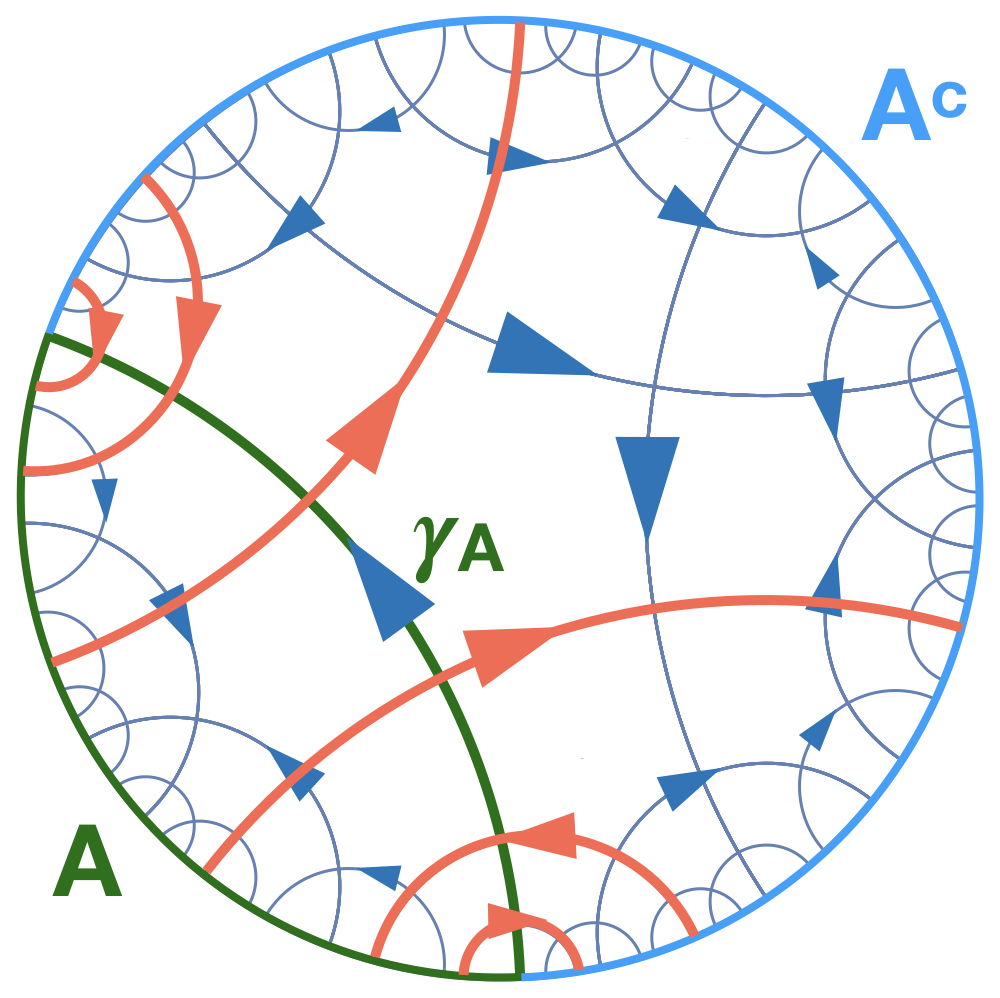
Fig.1 The bit-thread web emerging from the rank-2 U(1) gauge theory. Each thread carries entangled information shared by two boundary points. It is the condensation of these bit threads on geodesics of a negatively-curved space time which approximates the entanglement structure of holography at leading order.
2. Exotic states of matter mimicking the entanglement features of gravity
“Emergence” is a fascinating theme in condensed matter physics: many exotic theories that were invented to understand the fundamental constituents and interactions of the universe are found to exist in many-body systems --- not as the microscopic laws but as collective phenomena. It is thus intriguing to ask, are there any many-body systems that mimic gravity? In particular, can they mimic the informational properties of gravity like the entanglement structure, instead of the field-aspect ones like gravitons?
In this project, we give an affirmative answer, thanks to the recent development in understanding some exotic forms of matter called fracton states. Unlike conventional many-body systems where the global and local symmetries play the crucial role of determining their properties, the fracton states of matter have subsystem symmetries, which operate on a lower-dimensional space of the system, but not locally. Such systems were found to satisfy a few essential properties of gravity in the context of holography or AdS/CFT. That is, when embedded in the space of negative curvature, the fracton model shows very similar entanglement structure to gravity.
As a sequel to our first paper, making the initial discovery, the second paper provides more in-depth insight into the physics. We show that in a dual language of the system told in vertices and arrows, the fracton model is equivalent to a web of bit-threads — a well-known toy model construction widely used by people who study AdS/CFT. The dual description also helps us to quantify the holography breaking at finite temperature and the black hole microstate degrees of freedom.
This work leads to a universal picture of different toy models (tensor-networks, bit-threads, fracton states) with the advantage of known bulk theory. Hopefully, it will help us to make a more solid connection between toy models and genuine gravity.
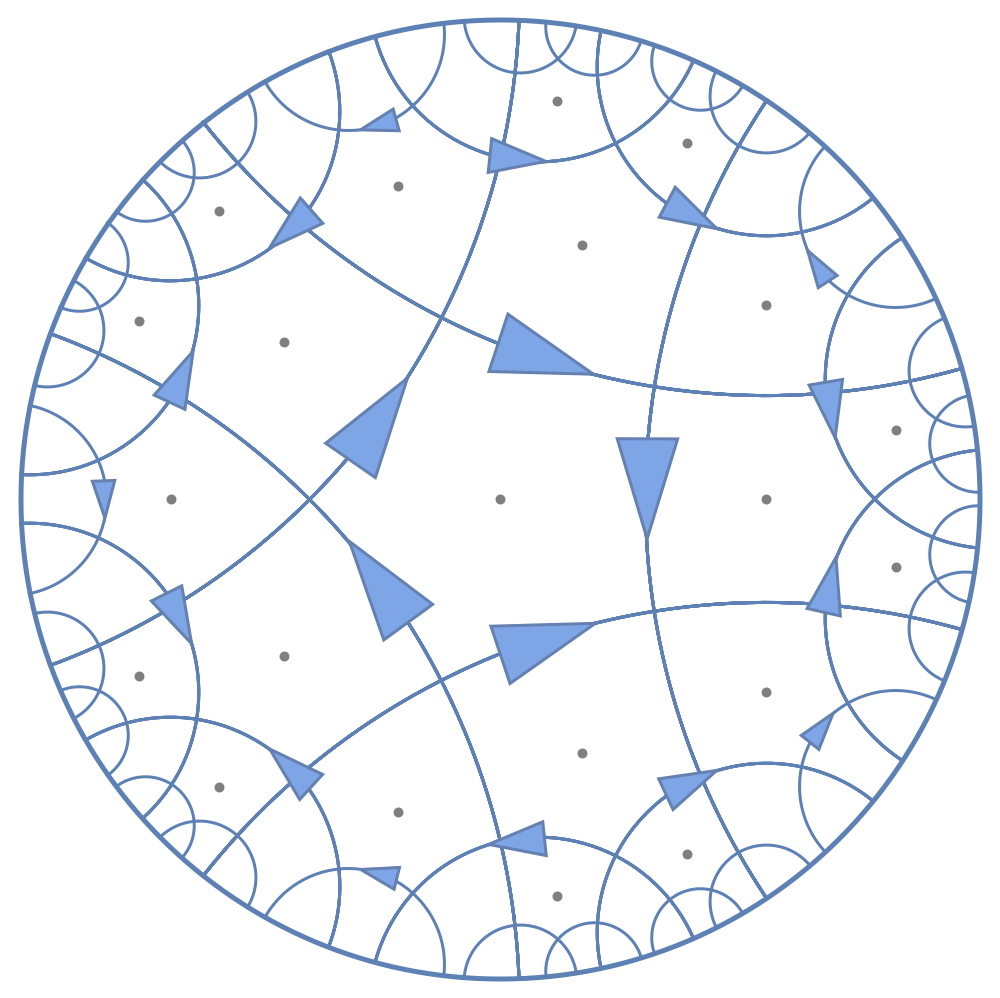
Fig.2 The dual eight vertex model at zero temperature. Each geodesic carries a binary arrow as one bit of information. It can be viewed as a bit thread. The web of evenly distributed bit threads satisfy the Ryu-Takayanagi formula of entanglement entropy of the boundary.
This work was published in the article: "Hyperbolic Fracton Model, Subsystem Symmetry, and Holography II: The Dual Eight-Vertex Modelar" Han Yan, Rev. B 100, 245138 (2019)
3. Interpreting frustrated magnets: man versus machine
Machine learning has already revolutionised the way we think about tasks as complex as driving a car. But can machines also do science ? In this project, we revisit a challenging problem in condensed-matter physics, the determination of the phase diagram of frustrated magnet, originally studied by Taillefumier et al., [Phys. Rev. X 7 041057 (2017)] (cf. FY2016 Annual Report). The model in question is the XXZ model on a pyrochlore lattice, and the particular challenge lies in the fact that this supports three different types of spin liquid phases, as well as both conventional, and unconventional forms of magnetic order (cf. upper panel of Fig.).
The machine learning method used was a Support Vector Machine (SVM) with a tensorial kernel (TK) and graphical analysis, previously introduced by J. Greitemann et al. [Phys. Rev. B 99, 060404(R) (2019)]. This method of machine learning does not require the machine to be "trained" on established examples, and can be "interpreted", i.e. it is possible to interrogate the machine about how it reached its final decision. Starting from spin configurations taken from classical Monte Carlo simulation, the TK-SVM correctly identified all of the phases found by Taillefumier et al. without any prior information about the type of phases present, completely reproducing the published phase diagram (cf. lower panel of Fig.1) . Moreover, the machine also correctly identified the organisational principle behind each phase, determining the correct order parameters for each of the ordered phases, and the correct local constraint for each of the spin liquids.
The striking success of the TK-SVM in this case suggests that it will be possible to solve the phase diagrams of complex models without human input.
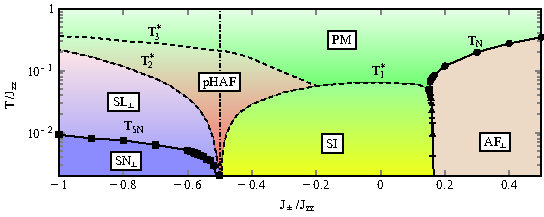
Fig.3(upper panel): Phase digram of the XXZ model on a pyrochlore lattice, as published by Taillefumier et al. [Phys. Rev. X 7, 041057 (2017)]. The phase digram is shown as a function of temperature and transverse exchange; three different forms of spin liquid compete with both magnetic and spin--nematic order.
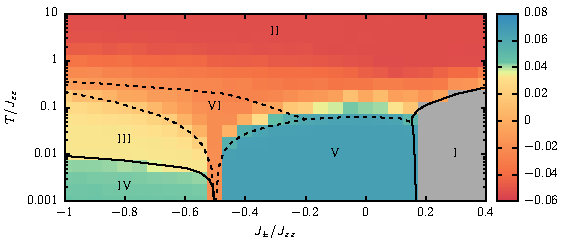
Fig.3(lower panel): Phase digram of the XXZ model on a pyrochlore lattice, as determined by machine learning, in the study by J. Greitemann et al. [Phys. Rev. B 100, 174408 (2019)]. The machine correctly identifies the same six phases as were found in the original study by Taillefumier et al., including three different types of spin liquids.
This work was a collaboration between members of the TQM Unit (OIST), members of the Theoretical Nanophysics Group (LMU Munich), and Dr Ludovic Jaubert of LOMA (CNRS Bordeaux). It was published as: "Identification of hidden order and emergent constraints in frustrated magnets using tensorial kernel methods", Jonas Greitemann, Ke Liu, Ludovic D.C. Jaubert, Han Yan, Nic Shannon, Lode Pollet, Phys. Rev. B 100, 174408 (2019)
4. Polarization Plateaus in Hexagonal Water Ice Ih
The most common form of Ice on earth can be considered as a paragon of geometric frustration. In the 1930s experiments revealed a discrepancy in the entropy between spectroscopic measurements and when integrating over the specific heat. This discrepancy stems from an extensive residual entropy caused by the ice rules: a single proton is placed on each of the four oxygen-oxygen link per oxygen site. There are two protons bonded covalently to each oxygen ion forming H2O molecules, while the two other protons form hydrogen bonds. As such the ice rules impose local constraints that prevent the H2O molecules from ordering and leave an extensively degenerate proton subsystem with a finite residual entropy.
In this study, we have been considering a minimal model of hexagonal Ice Ih and how an external electric field affects the proton configuration. Depending on the direction the field is applied, the extensive degeneracy of the proton configurations is either fully or only partially lifted. The latter occurs if the field is applied along certain easy axis and a polarization plateau at intermediate polarization is observed. The remaining ground states within these intermediate polarization plateaus can be described in terms of dimer models on the honeycomb and the square lattice, respectively. Upon tilting the external field slightly away of these easy axis, we observe an order-disorder transition of Kasteleyn type into a plateau at saturated polarization and vanishing entropy. In this work, the transition has been investigated analytically using the Kasteleyn matrix approach and numerically using a modified directed-loop Monte Carlo simulation.
While the emergent dimers on a honeycomb lattice are known from pyrochlore spin ice in a magnetic field, the emergent dimers on a square lattice are due to the different lattice structure of Ice Ih. It remains an interesting question, whether the intermediate polarization plateaus can be observed experimentally in Ice Ih.
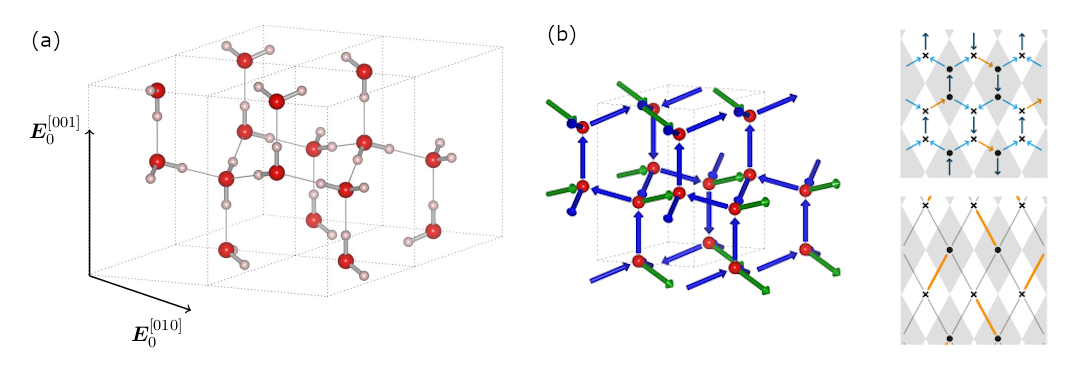
(a) Structure of Ice Ih and the two field directions considered.
(b) Upon applying the field along the [010] axis, a polarization plateau at intermediate polarization exists in which the remaining degrees of freedom (blue spins) map to dimers on a rhombic lattice.
This work was published in the article: "Polarization plateaus in hexagonal water ice Ih" Matthias Gohlke, Roderich Moessner, and Frank Pollmann, Phys. Rev. B 100, 014206 (2019)
5. Putative spin-nematic phase in BaCdVO(PO4)2
Like Volborthite, described below, BaCdVO(PO4)2 is a quasi-two dimensional magnet, with competing ferromagnetic and antiferromagnetic interactions. In such systems, it has been proposed that a new state of matter, known as a "spin nematic", can occur in high magnetic fields. BaCdVO(PO4)2 has previously been discussed as a candidate for spin-nematic order [A. Smerald, H. T. Ueda, and N. Shannon, Phys. Rev. B 91, 174402 (2015)], but until now, relatively little has been known about the experimental phase diagram of this material.
In this paper, we identify for the first time the nature of the magnetic grounds state of BaCdVO(PO4)2 in the absence of magnetic field, and present evidence for the existence of a novel magnetic phase in applied magnetic field, consistent with predictions of spin-nematic order. Evidence in support of this conclusion comes from elastic neutron scattering and dynamical susceptibility measurements on powder samples of BaCdVO(PO4)2. These results, in combination with recent thermodynamics measurements on single crystals [K. Y. Povarov, V. K. Bhartiya, Z. Yan, and A. Zheludev, Phys. Rev. B 99, 024413 (2019)], establish BaCdVO(PO4)2, like Volborthite, as a strong candidate for spin-nematic order.
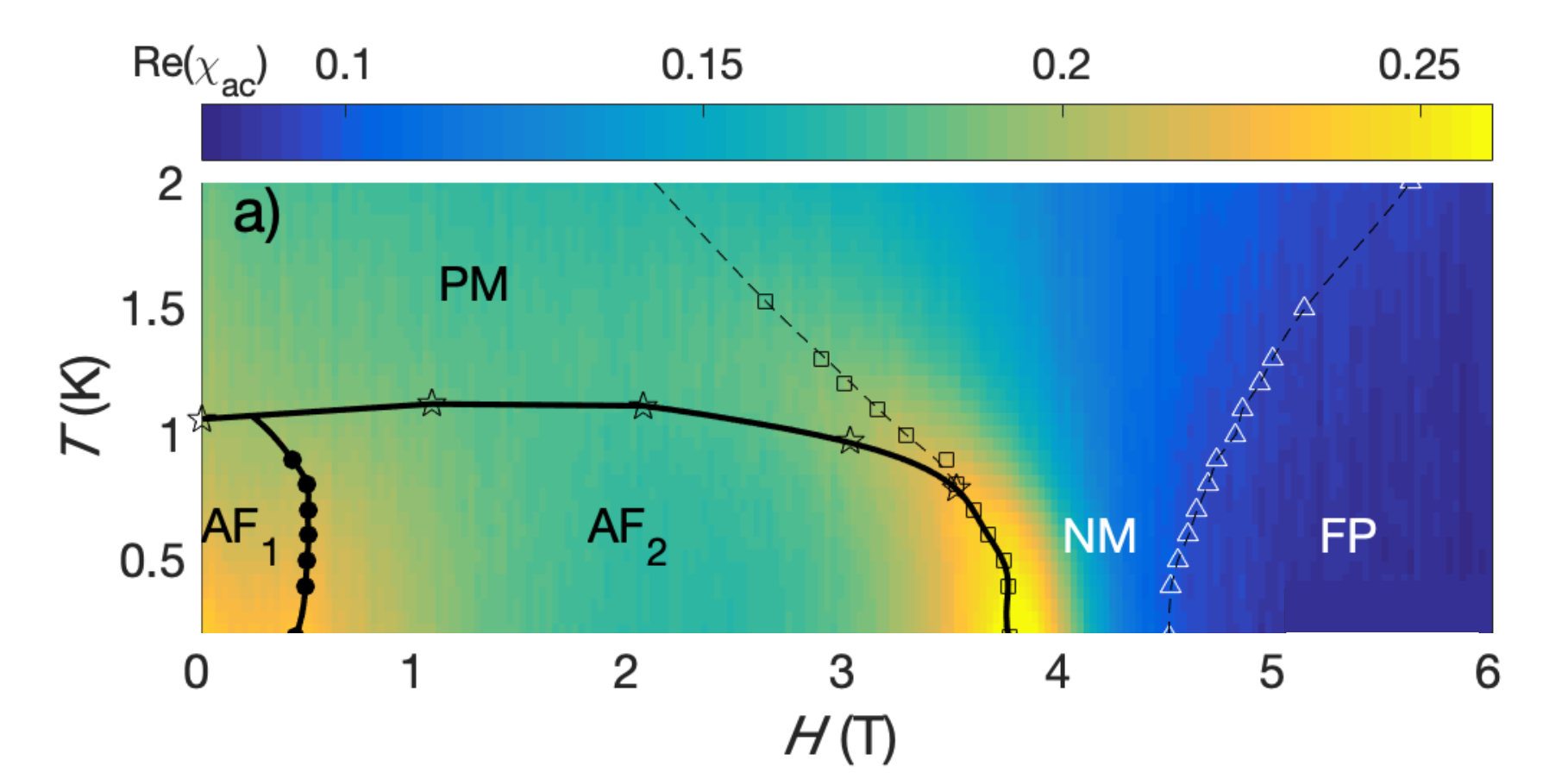
Fig.5 Magnetic phase diagram of BaCdVO(PO4)2, as determined by measurements of magnetic susceptibility, showing how conventional magnetic order vanishes for fields approaching 4T, providing evidence for a new non-magnetic phase where spin-nematic order has been predicted.
This work was published in the article: "Putative spin-nematic phase in BaCdVO(PO4)2" M. Skoulatos, F. Rucker, G.J. Nilsen, A. Bertin, E. Pomjakushina, J. Ollivier, A. Schneidewind, R. Georgii, O. Zaharko, L. Keller, Ch. Rüegg, C. Pfleiderer, B. Schmidt, N. Shannon, A. Kriele, A. Senyshyn, and A. Smerald, Phys. Rev. B 100, 014405 (2019)
6. Chaotic few-body vortex dynamics in rotating Bose-Einstein condensates
Chaotic phenomena in physics are ubiquitous and numerous examples exist in the natural world as soon as one goes beyond the classical two-body problem. These are interesting because while the equations of motion are known, the solutions are generally not known analytically, and their evolution is hard to predict.
In this study we tracked the trajectories of 4 vortices in a Bose-Einstein condensate and identified chaotic behavior arising when one of the vortices had opposite winding as compared to the others. Chaotic behavior is generally observed most strongly when three or more vortices are in the vicinity of each other. These collisional events appear to be the main cause of chaotic behavior in Bose Einstein condensates we investigated.
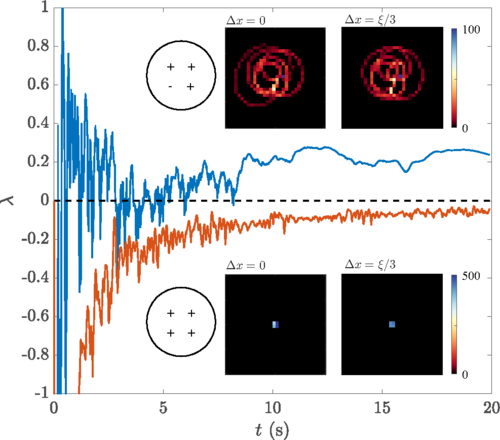
Fig.6 : The insets show the histograms of the COM trajectories calculated over 20 s of evolution for the system of four vortices when the position of a single vortex has been shifted by Δx=0ξ and Δx=ξ/3. The upper two panels depict the corresponding trajectories after the direction of rotation of a single vortex has been reversed, whereas the lower row displays the trajectories for the case where all vortices corotate. The main curve plots the corresponding Lyapunov exponents, calculated from the shown COM trajectories. The negative Lyapunov exponents (orange) indicate that shifting the vortex about the initial position still ensures the stability of vortex trajectories. Reversing the direction of circulation of a single vortex (blue) however leads to fluctuations about zero, eventually leading to a fully positive exponent.
This work was published in the article: "Chaotic few-body vortex dynamics in rotating Bose-Einstein condensates", Tiantian Zhang, James Schloss, Andreas Thomasen, Lee James O'Riordan, Thomas Busch, and Angela White, Phys. Rev. Fluids 4, 054701 (2019).
7. Possible observation of quantum spin-nematic phase in the frustrated magnet volborthite
Every child learns that water freezes in the cold of winter, and evaporates quickly in the heat of summer. Scientifically, these transformations between solid, liquid and gas are called phase transitions, and the fact that the same atoms can exhibit different phases lies at the heart of our understanding of the material world. A fourth phase of matter was discovered, by chance, late in 19th century, when Freiedrich Reinitzer tried to make crystals from molecules of cholesterol. Reinitzer noticed that as he cooled his solution of cholesterol towards its freezing point, it underwent a marked change in its physical properties, while remaining a liquid. This was the first observation of a "liquid crystal", a phase of matter in which rod- or disk-shaped molecules align like the atoms in a solid, while continuing to flow like a liquid.
Liquid crystals have since become an important part of every-day life, and are integral to the displays in most electronic devices. Meanwhile, the search for new phase of matter, including quantum analogies of liquid crystals, has become an increasingly important field of research. One long-sought example is the "quantum spin nematic", in which the quantum state of magnetic atoms mimic the rod-like molecules of a nematic liquid crystal. The possibility of this new phase of matter was first pointed half a century ago [M. Blume and Y. Y. Hsieh J Appl Phys 40, 1249 (1969); A. F. Andreev, I. A. Grishchuk, J Exp Theor Phys 97, 467 (1984)]. And it is now well understood how competing, or "frustrated", interactions between the ions in a magnet can give rise to a spin-nematic phase [A. V. Chubukov, Phys. Rev. B 44, 4693 (1991); N. Shannon et al., Phys. Rev. Lett., 96, 027213 (2006)]. None the less, despite their considerable interest, quantum spin nematics have proved very difficult to observe in experiment.
In this work, we report the possible observation of a quantum spin nematic in the naturally occuring mineral, volborthite. Volborthite contains copper atoms which are magnetic, with interactions of type needed to promote a spin-nematic state in high magnetic field [O. Janson et al., Phys. Rev. Lett. 117, 037206 (2016)]. We have probed the magnetic behaviour of the copper atoms by carrying out high-precision measurements of the way in which crystals of volborthite absorb heat, in fields of up to 33 Tesla. The results we find are consistent with the existence of a quantum spin-nematic phase, at temperatures below 1.5 Kelvin, for magnetic fields ranging from 25.5 to 27.5 Tesla.
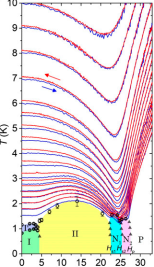
Fig.7 Magnetic phases found in volborthite in magnetic field of up to 33 Tesla, as determined by measurements of the magnetocaloric effect and specific heat. The phase marked "N2", occurring for temperatures below 1.5 Kelvin, bears the hallmarks of a spin nematic phase.
This work was published in the article: "Possible observation of quantum spin-nematic phase in a frustrated magnet", Yoshimitsu Kohama, Hajime Ishikawa, Akira Matsuo, Koichi Kindo, Nic Shannon, and Zenji Hiroi, Proc. Natl. Acad. Sci. 116, 10686 (2019).
4. Publications
4.1 Journals
- Han Yan, Owen Benton, Ludovic D.C. Jaubert and Nic Shannon, Rank-2 U(1) spin liquid on the breathing pyrochlore lattice, doi: 10.1039/Phys. Rev. Lett. 124.127203 (2020)
- Han Yan, Hyperbolic Fracton Model, Subsystem Symmetry, and Holography II: The Dual Eight-Vertex Model, doi: 10.1103/PhysRevB.100.245138 (2019)
- Tokuro Shimokawa, Tsuyoshi Okubo and Hikaru Kawamura, Multiple-q states of the J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet under magnetic fields, doi: 10.1103/PhysRevB.100.224404 (2019)
- Jonas Greitemann, Ke Liu, Ludovic D.C. Jaubert, Han Yan, Nic Shannon and Lode Pollet, Identification of emergent constraints and hidden order in frustrated magnets using tensorial kernel methods of machine learning, doi: 10.1103/PhysRevB.100.174408 (2019)
- Matthias Gohlke, Roderich Moessner, and Frank Pollmann, Polarization plateaus in hexagonal water ice Ih, doi: 10.1103/PhysRevB.100.014206 (2019)
- M. Skoulatos, F. Rucker, G.J. Nilsen, A. Bertin, E. Pomjakushina, J. Ollivier, A. Schneidewind, R. Georgii, O. Zaharko, L. Keller, Ch. Rüegg, C. Pfleiderer, B. Schmidt, N. Shannon, A. Kriele, A. Senyshyn, and A. Smerald, Putative spin-nematic phase in BaCdVO(PO4)2, doi: 10.1103/PhysRevB.100.014405 (2019)
- Tokuro Shimokawa, and Hikaru Kawamura, Ripple state in the frustrated honeycomb-lattice antiferromagnet, doi: 10.1103/PhysRevLett.123.057202 (2019)
- L. Rossi, A. Bobel, S. Wiedmann, R. Küchler, Y. Motome, K. Penc, N. Shannon, H. Ueda, and B. Bryant, Negative thermal expansion in the plateau state of a magnetically-frustrated spinel, doi: 10.1103/PhysRevLett.123.027205 (2019)
- Y. Kohama, H. Ishikawa, A. Matsuo, K. Kindo, N. Shannon and Z. Hiroi, Possible observation of quantum spin nematic phase in a frustrated magnet, doi: 10.1073/pnas.1821969116 (2019)
- Han Yan, Hyperbolic fracton model, subsystem symmetry, and holography, doi: 10.1103/PhysRevB.99.155126 (2019)
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
Invited Talks at Conference
- Matthias Gohlke "Field Induced Pseudo-Goldstone Mode and Nematic States in Kitaev Magnets" 3rd Asia-Pacific Workshop on Quantum Magnetism, Shanghai, China (2019.11.18)
- Han Yan "Fracton States of Matter as Toy Models of Holography" Youth Symposium on Theoretical High Energy Physics, Southeast University, China, (2019.08.21)
- Nic Shannon "Quantum Liquid Crystals in Magnets" Kickoff Meeting: Quantum Liquid Crystals, Tokyo, Japan (2019.08.19)
- Nic Shannon "From half moons to Chern numbers" TEMM and the joint TCM-magnetism IoP symposium, Abigdon, UK (2019.07.17)
- Judit Romhanyi "Topologically nontrivial excitations in quantum magnets" Competing Interactions and Colossal Responses in Transition Metal Compounds, Telluride Intermediate School, Colorado, USA (2019.06.27)
- Nic Shannon "An Introduction to Quantum Spin Liquids" 3rd TRR 80 Summer School" Functionality of Correlated Materials, Germany (2019.06.27)
Contributed Talks
- Tokuro Shimokawa "Finite and zero temperature physics in the S=1/2 bilayer breathing-kagome magnet", 第14回量子スピン系研究会, Akita, Japan (2020.01.08)
- Tokuro Shimokawa "Finite-temperature properties of the S=1/2 Shastry-Sutherland model" The Physical Society of Japan, Gifu, Japan (2019.09.13)
- Matthias Gohlke "Dynamical and Topological Properties of the Kitaev Model in a [111] Magnetic Field" 2019 Autumn Meeting, The Physical Society of Japan, Gifu, Japan (2019.09.13)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice antiferromagnet" Computational Approaches to Quantum Many-body Problems (CAQMP), ISSP, The University of Tokyo, Japan (2019.07.22)
- Nic Shannon "Designer spin liquids" DPG Fall Meeting, Regensburg 2019, Germany (2019.04.01)
Seminars
- Han Yan "Fracton States of Matter as Toy Models of Holography" Princeton Center for Theoretical Science, Princeton University, USA (2019.11.21)
- Han Yan "Rank–2 U(1) spin liquid on the breathing pyrochlore lattice" Condensed Matter Theory Seminar, MIT, USA (2019.11.12)
- Han Yan "Fracton States of Matter as Toy Models of Holography" Center for Theory of Quantum Matter, University of Colorado Boulder, USA (2019.10.25)
- Han Yan "Hyperbolic fracton model, subsystem symmetry, and holography" High Energy Accelerator Research Organization (KEK), Ibaraki, Japan (2019.09.19)
- Han Yan "Rank-2 U(1) spin liquid on the breathing pyrochlore latticeRank-2 U(1) spin liquid on the breathing pyrochlore lattice" Condensed Matter Theory Group, Paul Scherrer Institute, Switzerland (2019.08.06)
- Han Yan "Fracton Model and Holography" Condensed Matter Theory Group Technical University of Munich, Germany, (2019.08.01)
- Han Yan "Fracton Model and Holography" LOMA, University of Bordeaux, France (2019.07.23)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice Heisenberg antiferromagnet" Tokyo University of Science, Tokyo, Japan (2019.07.19)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice Heisenberg antiferromagnet" Technical University of Munich, Munich, Germany (2019.06.06)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice Heisenberg antiferromagnet" Helmholtz-Zentrum Dresden-Rossendorf, Dresden, Germany (2019.06.04)
- Judit Romhanyi "Hall responses in larger spin quantum magnets" RIKEN, Saitama, Japan (2019.06.03)
- Nic Shannon "Designer spin liquids" Laboratoire de Physique Théorique, Toulouse, France (2019.05.23)
- Nic Shannon "A Hitchiker's Guide to Frustrated Magnets" LOMA of the University of Bordeaux, France (2019.05.21)
- Nic Shannon "Designer spin liquids" MPI for Solid State Research, Germany (2019.05.16)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice Heisenberg antiferromagnet" RIKEN, Japan (2019.05.15)
- Nic Shannon "An Introduction to Quantum Spin Nematics" ETH Zürich, Hönggerberg, Switzerland (2019.05.09)
- Nic Shannon "Designer spin liquids" University of Oxford, UK (2019.04.16)
Poster Presentations
- Nic Shannon "Theory of Quantum Matter Unit" OIST-Hitachi joint symposium, Hitachi R&D, Japan (2020.02.17)
- Tokuro Shimokawa "Ground state and thermodynamic properties of the S=1/2 bilayer breathing-kagome Heisenberg magnet" Computational Approaches to Quantum Many-body Problems (CAQMP) 2019 , Kashiwa, Japan (2019.08.05)
- Geet Rakala "Hard plates on a cubic lattice" Statphys 27, Buenos Aires, Argentina (2019.07.10)
- Han Yan "Fracton Model and Holography" YITP, Kyoto University, Japan (2019.06.12)
5. Intellectual Property Rights and Other Specific Achievements
-
APS TV Film : Film about the TQM Unit commisioned for APS TV, and made to be shown at the 2020 March Meeting of the American Physical Society.
6. Meetings and Events
Seminar
6.1 Hopfions in 3D dimer models
- Date: March 26, 2020
- Venue: Zoom Seminar
- Speaker: Dr. Grigory Bednik (University of California Santa Cruz, USA)
6.2 First-principles study for material science
- Date: March 10, 2020
- Venue: OIST Campus Lab3
- Speaker: Associate Prof. Yasutomi Tatetsu (University Center for Liberal Arts Education, Meio University, Japan)
6.3 Quantum spin liquid candidate Ca10Cr7O28 – A spinon description
- Date: February 18, 2020
- Venue: OIST Campus Lab3
- Speaker: Mr. Jonas Sonnenschein (Freie University of Berlin, Germany)
6.4 Magnetic Field Induced Competing Phases in Kitaev Magnets
- Date: January 22, 2020
- Venue: OIST Campus Lab1
- Speaker: Dr. Ryui Kaneko (Institute for Solid State Physics, University of Tokyo, Japan)
6.5 Numerical simulations of spin-1 magnets
- Date: April 25, 2019
- Venue: OIST Campus Lab1
- Speaker: Dr. Rico Pohle (Waseda University, Japan)
6.6 Finite-temperature spectra of spin-orbit coupled Mott insulators
- Date: April 24, 2019
- Venue: OIST Campus Lab1
- Speaker: Prof. Youhei Yamaji (Department of Applied Physics, the University of Tokyo, Japan)
6.7 Representation of Quantum Many-body System by Neural Networks
- Date: April 17, 2019
- Venue: OIST Campus Lab2
- Speaker: Mr. Nobuyuki Yoshioka (University of Tokyo, Katsura group, Japan)
7. Other
Nothing to report.



