FY 2024 Research & Annual Reports

The Theory of Quantum Matter (TQM) Unit carries out research into a wide range of problems in condensed matter and statistical physics, with an emphasis on the novel phases of matter found in frustrated magnets. Other topics of current interest include the application of machine learning to problems in physics, and algorithmic aspects of quantum computing.
This work is described in the Annual Reports listed in the menu on the left side of this page. These provide details of all of the research carried out by the TQM Unit, publications and presentations by Unit members, outreach activity, and seminars given by visitors to TQM in OIST. Reports are organised by the Japanese financial year, with FY2023 running from April 1st 2023 until March 31st 2024.
Recent research results, and preprints, are described below.
Phase transitions in quantum control landscapes
Quantum computation requires reliable preparation of particular initial states. In general, this is a difficult process due to limitations of the operations experimentalists can apply on qubits to change their state and practical imperfections which may arise from the apparatus used. We have investigated the space of possible protocols which may be used in a realistic setting and found that the protocols which lead to a successful preparation of the required state (called optimal protocols) break up into different connected families. Within one family, individual protocols can be smoothly transformed into each other using local modifications. The characteristics of such protocols are controlled by multiple parameters present in the experimental setup, and for our work we have focused only on the total time allowed for the evolution of the state (T). As a function of T, we find phase transitions between regimes where we have isolated optimal protocols and where extended families of protocols exist. This finding suggests that there is an entirely new set of transitions to investigate in the space of protocols for quantum control problems.
We have used a variety of analytical and numerical techniques borrowed from statistical mechanics to analyze these phase transitions and also studied realistic protocols which comprise of pulse sequences of magnetic fields. We have analyzed single and two qubit systems in detail and found a fundamentally new type of phase transition (topological in nature) for the latter. Our techniques can be extend to few-qubit systems in a straightforward manner."
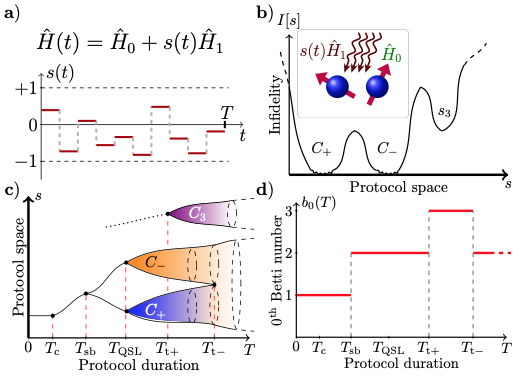
Figure caption : control landscape in Eq. (1). a) Piecewise-constant protocols s(t) control a system H_0 by modulating the external drive H_1 for a total duration T (inset panel (b)). b) Illustration of the optimization landscape I[s] for a fixed protocol duration T . Depending on T, the landscape possesses a different number of basins of attraction; in this schematic, two basins are associated with the connected components C+,C− of the infinite- dimensional optimal level set and one with the local trap s3. c) Sketch of the optimal level set {arg min_s I[s]} as a function of T. Topological transitions at Tsb, Tt+ and Tt– marks sudden change in the number of connected components b_0(T). d) Topological CLPTs correspond to jump-discontinuities of a topological invariant known as the 0th Betti number b_0(T) as a function of T; the T_QSL transition does not affect b_0(T).
This work is described in the preprint "Topological phase transitions in a constrained two-qubit quantum control landscape" Nicolò Beato, Pranay Patil, and Marin Bukov, arXiv:2411.08736, and "Towards a theory of phase transitions in quantum control landscapes", Nicolò Beato, Pranay Patil, and Marin Bukov, arXiv:2408.11110
Witnessing Disorder in Quantum Magnets
There are no clean samples in nature. Therefore, when we come to discuss the entanglement properties of quantum materials, the effects of disorder must be taken into account. This question is of particular interest for high-entangled states, such as quantum spin liquids, which lie outside the Landau paradigm for classifying phases of matter. In this work, we explore what experimentallyaccessible measures, in the form of concurrence, residual tangle and quantum Fisher information, can teach us about the entanglement in the presence of disorder. As a representative example, we consider the Tomonaga-Luttinger liquids (TLL) and disorder-driven random singlet (RS) states found in antiferromagnetic quantum spin chains. Using quantum Fisher information and residual tangle, we demonstrate that both TLL and RS states exhibit multi-partite entanglement. In the case of the RS state, we attribute this to entanglement localized below a crossover length scale. We further show that the order of disorder average matters in calculating measures like concurrence, and that this can lead to false inferences when interpreting experiment. None the less, correctly interpreted, these witnesses provide useful information about the effects of disorder. We explore how information about the central charge of the TLL can be extracted from the low-temperature behavior of concurrence, and conjecture that this analysis can be extended to the effective central charge of the RS state. Finally, we establish how RS and TLL states can be distinguished through the growth of multi-partite entanglement, as witnessed by the equal-time structure factor. These results establish that, used carefully, experiments based on entanglement witnesses can provide important information about quantum spin systems in the presence of disorder.
This work is described in the preprint, "Witnessing Disorder in Quantum Magnets", Snigdh Sabharwal, Tokuro Shimokawa, and Nic Shannon, arXiv:2407.20797
Magnon Spectra of Cuprates beyond Spin Wave Theory
The usual starting point for understanding magnons in cuprate antiferromagnets such as La$_2$CuO$_4$ is a spin model incorporating cyclic exchange, which descends from a one–band Hubbard model, and has parameters taken from fits based on non–interacting spin wave theory. Here we explore whether this provides a reliable description of experiment, using matrix product states (MPS) to calculate magnon spectra beyond spin wave theory. We find that analysis based on low orders of spin wave theory leads to systematic overestimates of exchange parameters, with corresponding errors in estimates of Hubbard t/U. Once these are corrected, the “standard” model provides a good account of magnon dispersion and lineshape in La$_2$CuO$_4$, but fails to fully capture the continuum observed at high energies. The extension of this analysis to CaCuO$_2$ and Sr$_2$IrO$_4$ is also discussed.
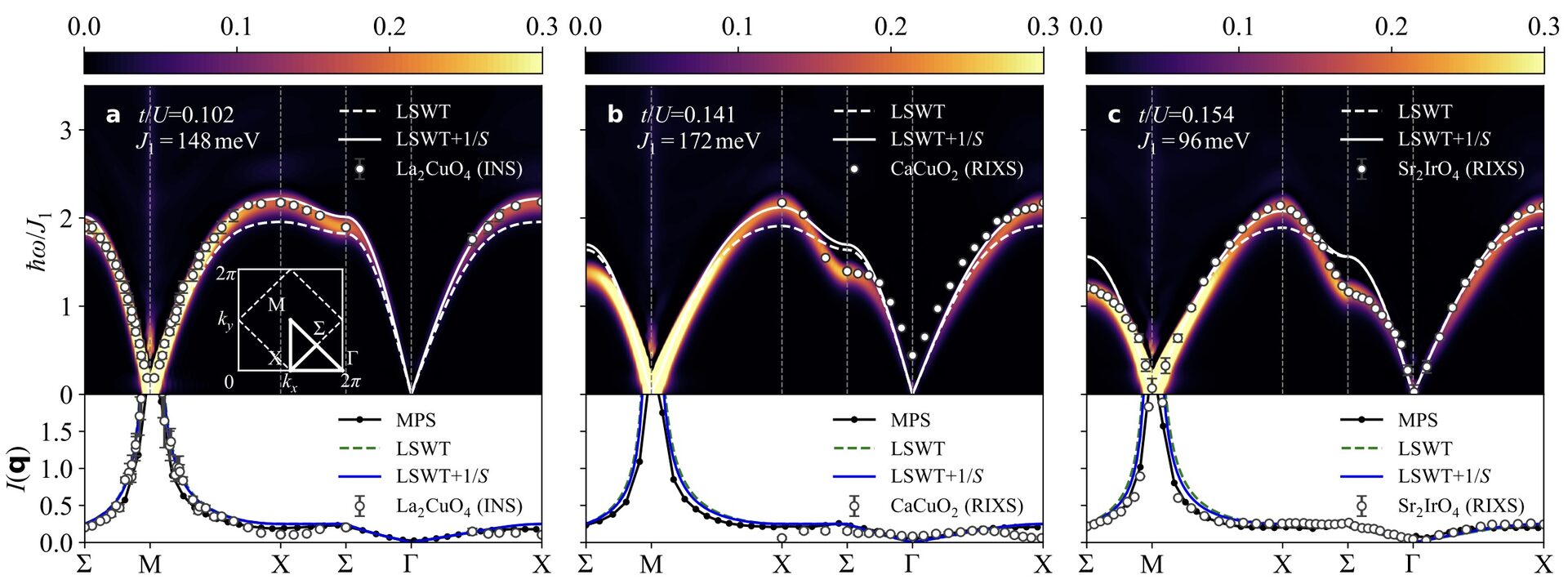
This work is described in the preprint, "Magnon Spectra of Cuprates beyond Spin Wave Theory", Jiahui Bao, Matthias Gohlke, Jeffrey G. Rau, and Nic Shannon arXiv:2407.20501
Candidate quantum spin liquids on the maple-leaf lattice
Quantum spin liquids (QSLs) are a class of exotic phases where spins do not exhibit traditional magnetic order, typically due to the absence of a local order parameter. This lack of conventional order makes QSLs difficult to study using traditional methods like Landau’s theory of phase transitions. Instead, QSLs are understood as phases that feature emergent gauge fields and fractionalized excitations known as spinons, which behave like independent particles with their own fractional quantum numbers. The framework of projective symmetry groups (PSG) allows us to classify these unconventional states by extending the symmetry of the system to account for the emergent gauge fields. By using this approach, we can systematically study quantum spin liquids and apply a Landau-like classification to these phases, despite their lack of conventional order.
In this work, we focus on the maple-leaf lattice, a two-dimensional geometrically frustrated lattice that has recently drawn attention as a potential host for quantum spin liquids. Previous studies have suggested that the spin-1/2 Heisenberg model on this lattice may exhibit a quantum paramagnetic phase, possibly sandwiched between magnetically ordered and dimerized states. While these studies indicate the presence of a QSL phase, they have yet to clearly define the phase's characteristics, such as whether it is gapless or gapped, or whether it follows a U(1) or ℤ2 gauge structure. To address this, we apply the PSG framework, which allows us to classify the different possible QSL states based on their symmetries. We find a total of 17 U(1) and 12 ℤ2 distinct algebraic structures, and show that, when restricted to nearest-neighbor interactions, there are 12 U(1) and 8 ℤ2 realizable phases. Additionally, when considering interactions up to third neighbors, all possible U(1) and ℤ2 states become achievable.
Our analysis primarily focuses on singlet QSLs, but we also consider triplet fields, which could be important in describing real materials where competing ferromagnetic and spin-orbit couplings are present. These interactions can lead to a rich variety of topologically nontrivial states and spin nematic phases, which may be relevant for describing materials with maple-leaf lattice geometries or distortions. This work provides a systematic classification of potential QSL phases on the maple-leaf lattice, offering insights into the behavior of quantum spin liquids and setting the stage for future studies on these elusive phases of matter.

Figure caption: Different flux states on the maple leaf lattice.
This work is published as "Candidate quantum spin liquids on the maple-leaf lattice", Jonas Sonnenschein, Atanu Maity, Chunxiao Liu, Ronny Thomale, Francesco Ferrari, and Yasir Iqbal, Phys. Rev. B 110, 014414.
Eight-color chiral spin liquid in the S=1 bilinear-biquadratic model with Kitaev interactions
Multipolar spin systems provide a rich ground for the emergence of unexpected states of matter due to their enlarged spin degree of freedom.
In this study, with a specific emphasis on S = 1 magnets, we explore the interplay between spin nematic states and spin liquids. Based on the foundations laid in the prior work [R. Pohle et al., Phys. Rev. B 107, L140403 (2023)], we investigate the S = 1 Kitaev model with bilinear-biquadratic interactions, which stabilizes, next to Kitaev spin liquid, spin nematic and triple-q phases, also an exotic chiral spin liquid. Through a systematic reduction of the spin degree of freedom—from CP2 to CP1 and ultimately to a discrete eight-color model—we provide an intuitive understanding of the nature and origin of this chiral spin liquid. We find that the chiral spin liquid is characterized by an extensive ground-state degeneracy, bound by a residual entropy, extremely short-ranged correlations, a nonzero scalar spin chirality marked by Z2 flux order, and a gapped continuum of excitations. This work contributes not only to the specific exploration of S = 1 Kitaev magnets but also to the broader understanding of the importance of multipolar spin degree of freedom on the ground state and excitation properties in quantum magnets.
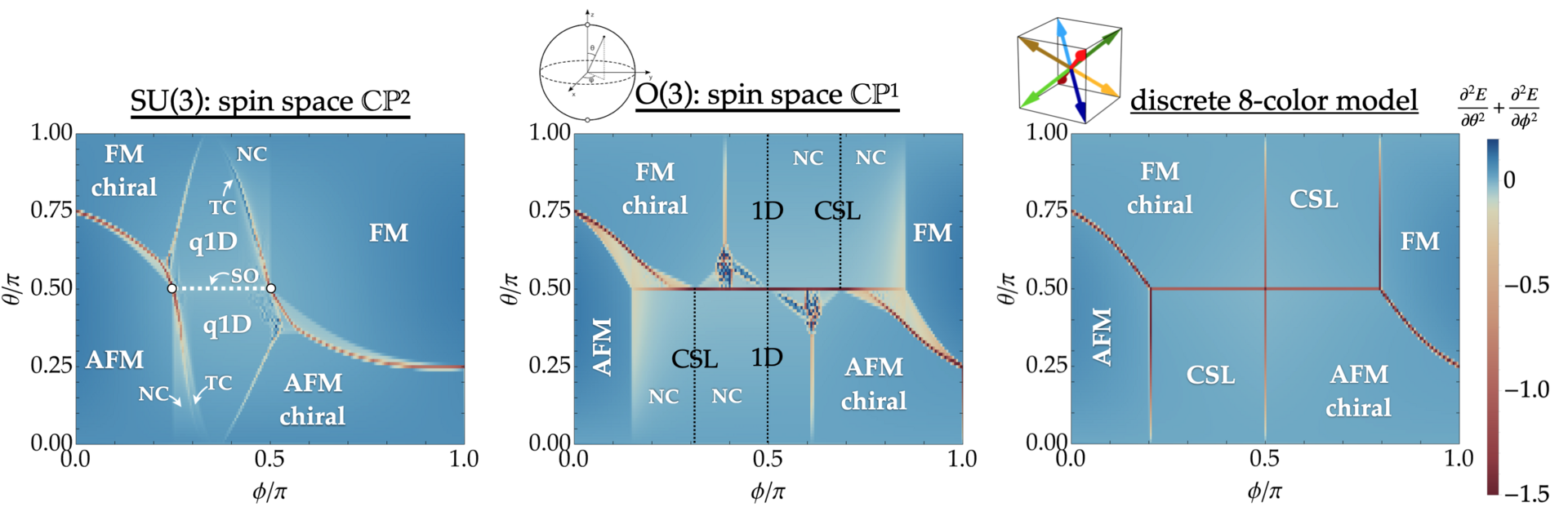
This work is published as "Eight-color chiral spin liquid in the S=1 bilinear-biquadratic model with Kitaev interactions", Rico Pohle, Nic Shannon, and Yukitoshi Motome, Phys. Rev. Research 6, 033077 (2024)



