FY2022 Annual Report
Theory of Quantum Matter Unit
Professor Nic Shannon

Abstract
FY2022 was a year in which the TQM Unit resumed international travel started receiving international visitors, following the reopening of Japan's borders.
In many ways the TQM Unit enjoyed a fortunate pandemic, able to work remotely in the calm and safety of Okinawa. However the price for this safety was a long isolation from international peers, which made the spontaneous exchange of scientific ideas, and recruitment of new staff, challenging. This changed on March 5th, 2022, when Japan's borders reopened to international travel by scientists with a valid visa.
An immediate consequence was the resumption of visits to OIST by scientists based outside Japan. Over the course of FY 2022, the TQM Unit hosted 20 seminars, with 9 of these given in-person, by visitors to the Unit. Topics for these seminars ranged from stratgeies for carrying out quantum chemistry calculations on a quantum computer, to statistical models of brain function.
Happily, the reopening of Japan's borders coincided with the general return of international conferences to an "in person" modality. As a consequence, members of the Unit started to travel internationally with something approaching historical frequency. In total Unit Members gave 20 invited talks at conferences and research institutes in FY 2022, and a further 18 contributed talks and posters. These included in-person presentations at events in America, England, Fracne, Germany, India, Japan and Switzerland.
The unit published 7 papers in peer-reviewed journals in FY2022, including papers in Physical Review Letters and Quantum Science and Technology, and an epic 40-page paper Physical Review Research. Research highlights included theories for novel spin liquids in both spin-1/2 and spin-1 Kitaev models, and further development of algorithms for NISQ-era quantum computers.
FY2022 also saw a number of other significant events in the life of the Unit. Notable amoung these was the succesful Thesis Defence of Dr Kimberly Remund; the award of an KAKENHI early-career grant to Dr Matthias Gohlke; the award of a KAKENHI grant within the "Extereme Universe" project to Dr Tokuro Shimokawa; and two separate poster prizes for Leilee Chojnacki, awarded for her work on the connection between gravitational waves and quantum liquid crystals.
1. Staff
- Dr. Matthias Gohlke, Staff Scientist
- Dr. Tokuro Shimokawa, Staff Scientist
- Dr. Geet Rakala, Postdoctoral Scholar
- Dr. Jonas Sonnenschein, Postdoctoral Scholar
- Mr. Jiahui Bao, PhD Student (2022 Jan -)
- Ms. Leilee Chojnacki, PhD Student
- Mr. Soshi Mizutani, PhD Student (non-study leave)
- Ms. Kimberly Remund, PhD Student
- Mr. Snigdh Sabharwal, PhD Student (2022 Jan -)
- Ms. Ananya Samanta, PhD Student
- Ms. Megumi Ikeda, Research Unit Administrator
- Ms. Chika Sparacio, Reseach Unit Administrator (2022 Nov -)
2. Collaborations
2.1 Search for Quantum Spin Liquids in Extended Kitaev Models
- Type of collaboration: Joint Research
- Researchers:
- Dr. Matthias Gohlke, OIST
- MSc. Jose-Carlos Pelayo, OIST
- Associate Prof. Takafumi Suzuki, University of Hyogo
2.2 Interaction-Induced Magnon Degeneracy Breaking
- Type of collaboration: Joint research
- Researchers:
- MSc. Alberto Corticelli, MPIPKS Dresden
- Dr. Matthias Gohlke, OIST
- Dr. Alexander Mook, Uni Basel
- Dr. Paul McClarty, MPIPKS Dresden
- Prof. Roderich Moessner, MPIPKS Dresden
2.3 Studying Quantum Magnets at Finite Temperature Using Tensor Networks
- Type of collaboration: Joint research
- Researchers:
- MSc. Atsushi Iwaki, University of Tokyo
- Dr. Matthias Gohlke, OIST
- Prof. Chisa Hotta, University of Tokyo
2.4 Modelling the Hydrogen Bond Network in Water
- Type of collaboration: Joint research
- Researchers:
- Dr. Geet Rakala, OIST
- Dr. Rahul Dandekar, IPTh, CEA/Saclay
- Prof. Ali Hassanali, ICTP, Trieste
- Prof. Nic Shannon, OIST
2.5 Analogues of Light and Gravity in the Collective Excitations of Quantum Magnets
- Type of collaboration: Joint research
- Researchers:
- MSc. Leilee Chojnacki, OIST
- Dr. Rico Pohle, University of Tokyo
- Dr. Han Yan, OIST & Rice University
- Prof. Nic Shannon, OIST
- Prof. Yutaka Akagi, University of Tokyo
2.6 Negative Thermal Expansion in a Magnetically Frustrated Spinel
- Type of collaboration: Joint research
- Researchers:
- MSc. Ananya Samanta, OIST
- Dr. Geet Rakala, OIST
- Dr. Han Yan, Rice University
- Prof. Karlo Penc, Institute for Solid State Physics and Optics, Wigner
Research Centre for Physics, Hungarian Academy of Sciences - Prof. Nic Shannon, OIST
2.7 Numerical Simulation of Spin-1 Magnets
- Type of collaboration: Joint research
- Researchers:
- MSc. Kimberly Remund, OIST
- Dr. Rico Pohle. University of Tokyo
- Prof. Yutaka Akagi, University of Tokyo
- Prof. Judit Romhanyi, University of California Irvine
- Prof. Nic Shannon, OIST
2.8 Generalization of SCGA to Spin-1 magnets
- Type of collaboration: Joint researcM
- Researchers:
- MSc. Kimberly Remund, OIST
- Dr. Owen Benton, MPI-PKS Dresden
- Prof. Nic Shannon, OIST
2.9 Monte Carlo Algorithms for Spin-1 Magnets
- Type of collaboration: Joint research
- Researchers:
- MSc. Kimberly Remund, OIST
- Dr. Geet Rakala, OIST
2.10 Development of the Exact Diagonalization Method for Near Saturation Fields
- Type of collaboration: Joint Research
- Researchers:
- Dr. Tokuro Shimokawa, OIST
- Prof. Daisuke Yamamoto, Nihon University
- Prof. Hiroshi Ueda, Osaka University
2.11 Algorithms for NISQ-era Quantum Computers
- Type of collabotaion: Joint Research
- Researchers:
- MSc. Yunlong Yu, Tsinghua University
- MSc. Chenfeng Cao, Hong Kong University of Science and Technology
- Prof. Xiang-Bin Wang, Tsinghua University
- Prof. Robert Joynt, UW-Madison
- Prof. Nic Shannon, OIST
2.12 High-field Magnetism in the S=1/2 Honeycomb-Lattice Antiferromagnet Cu2(pymca)3(ClO4)
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Tokuro Shimokawa, OIST
- Dr. Akira Okutani, Fukui University
- Prof. Zentaro Honda, Saitama University
- Prof. Takano Kenichi, Toyota Technological Institute
- Prof. Masayuki Hagiwara, Osaka University
2.13 Entanglement-Based Identification Between Quantum Spin Liquid State and Random Singlet State
- Type of collabotaion: Joint Research
- Researchers:
- MSc. Snigdh Sabharwal
- Dr. Tokuro Shimokawa, OIST
- Prof. Nic Shannon, OIST
2.14 Quantum Spin Nematic Order in Frustrated Ferromagnets
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Jonas Sonnenschein, OIST
- Dr. Matthias Gohlke, OIST
- Dr. Tokuro Shimokawa, OIST
- Prof. Nic Shannon, OIST
2.15 Spin Liquid in BKK Material Ca10Cr7O28
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Jonas Sonnenschein, OIST
- Dr. Tokuro Shimokawa, OIST
- Dr. Rico Pohle, The University of Tokyo
- Dr Han Yan, Rice
- Prof. Nic Shannon, OIST
2.16 Higher Dimensional SUSY Quantum Mechanics
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Jonas Sonnenschein, OIST
- Dr. Mirian Tsulaia, Quantum Gravity unit of Yashi Neiman
- Dr Aritra Banerjee, Quantum Gravity unit of Yashi Neiman
2.17 Projective Symmetry Group Classification of Quantum Spin Liquids on the Diamond Lattice
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Jonas Sonnenschein, OIST
- Prof. Yasir Iqbal, IIT Madras, India
2.18 Projective Symmetry Group Classification of Quantum Spin Liquids on the Maple Leaf Lattice
- Type of collabotaion: Joint Research
- Researchers:
- Dr. Jonas Sonnenschein, OIST
- Prof. Yasir Iqbal, IIT Madras, India
2.19 Machine learning approaches to frustrated magnets
- Type of collabotaion: Joint Research
- Researchers:
- Mr. Nicolas Sadoune, LMU
- Dr Ke Liu, LMU
- Prof. Lode Pollet, LMU
- Dr Han Yan, Rice
- Dr. Ludovic Jaubert, CNRS
- Prof. Nic Shannon, OIST
2.20 Parton approach to spin liquids on the pyrochlore lattice
- Type of collabotaion: Joint Research
- Researchers:
- Prof. SungBin Lee, KAIST
- Dr Hyeok-Jun Yang, KAIST
- Prof. Nic Shannon, OIST
3. Activities and Findings
3.1 Spin Nematics Meet Spin Liquids: Exotic Quantum Phases in the Spin-1 Bilinear-Biquadratic Model with Kitaev Interactions
New discoveries are often made on the border between different disciplines. One major discipline in solid state physics is dedicated to quantum spin liquids, an unconventional state of matter accompanied by emergent gauge fields, topological order, and fractionalized excitations. Another concept is that of spin nematics, a magnetically ordered state dominated by quadrupole moments, which breaks spin-rotation symmetry by selecting an axis, while not choosing a particular direction. Usually seen as two separate areas of study, we are interested in combining those two disciplines, by asking the question: “What happens, when a spin nematic and a spin liquid meet?”
To answer this question, we showed that the S=1 Kitaev model under the influence of bilinear-biquadratic interactions hosts many unconventional ordered and disordered phases. We obtain a comprehensive phase diagram including chiral ordered and quadrupolar ordered phases, in addition to already known ferro, antiferro, zigzag and stripy phases. Intriguingly, we find that the competition between Kitaev and positive biquadratic interactions also promotes a noncoplanar finite-temperature spin liquid state, with macroscopic degeneracy and finite scalar chirality.
Our results show that the competition between spin liquid and spin nematic phases is a promising way to explore new magnetic states of matter.
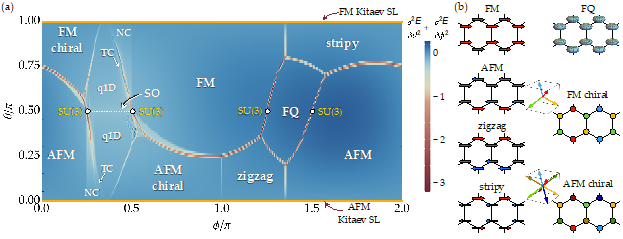
Figure: Ground state phase diagram of the S=1 Kitaev model under the influence of bilinear-biquadratic interactions hosts many ordered and disordered phases, such as ferromagnetic (FM), antiferromagnetic (AFM), zigzag, and stripy orders, and spin-nematic ferroquadrupolar (FQ) order. The competition between chiral magnetic order, the Kitaev spin liquid (SL), and quadrupolar semi-order (SO) gives rise to unconventional phases, such as the twisted conical (TC), quasi-one-dimensional (q1D) coplanar, and noncoplanar (NC) ordered phases.
This work was published as "Spin nematics meet spin liquids: Exotic quantum phases in the spin-1 bilinear-biquadratic model with Kitaev interactions", R. Pohle, N. Shannon, Y. Motome, Phys. Rev. B 107, L140403 (2023).
3.2 Extended Quantum Spin Liquid with Spinon-like Excitations in an Anisotropic Kitaev-Gamma Model
Quantum spin liquids have become an important research subject in condensed matter physics due to their exotic emergent properties: fractional excitations, topological order, emergent gauge fields, anyonic exchange statistics, etc. Kitaev's honeycomb model is a paradigmatic spin-1/2 model in this context, due to being exactly solvable and featuring a quantum spin liquid ground state in terms of itinerant Majorana fermions in a static \(\mathbb Z_2\) gauge field. The bond-dependent Kitaev spin-exchange is realized in certain magnets with strong spin-orbit coupling. This mechanism, however, introduces additional spin exchanges that spoil the exact solvability of the Kitaev model. Many candidate Kitaev materials have been proposed among which alpha-\(RuCl_3\) has gained much attention due to a putative QSL phase in an in-plane magnetic field, and even more so, since the measurement of a half-quantized thermal hall effect was reported suggesting the existence of emergent Majorana fermions. As a minimal model for alpha-RuCl_3, the spin-1/2 Kitaev-\(\Gamma (K\Gamma)\) model on the honeycomb lattice with ferromagnetic Kitaev exchange and positive symmetric off-diagonal \(\Gamma\) exchange has been proposed. Many different methods have been applied, yet no clear understanding of its quantum ground state has emerged. Among the suggested ground state phases are not only magnetically ordered states, such as zigzag, ferromagnet, six-sublattice, or incommensurate spiral order, but also quantum paramagnetic phases such as a putative gapped QSL, a lattice-nematic paramagnet, or a gapless QSL with multiple Majorana-Dirac nodes.
Within this project we like to change the perspective and focus instead on an aspect rarely included in theoretical works on Kitaev materials: we additionally tune the strength of the spin exchange spatially, ranging from a limit of uncoupled chains to spatially equal, yet still strongly anisotropic, spin exchange. In fact, such spatial anisotropy may either be intrinsic due to a reduced symmetry of the underlying lattice, such as \(C2/m\) instead of a full \(C_3\) rotational symmetry, or spatial anisotropy can be induced by applying external pressure or strain, which possibly realizes various different QSL.
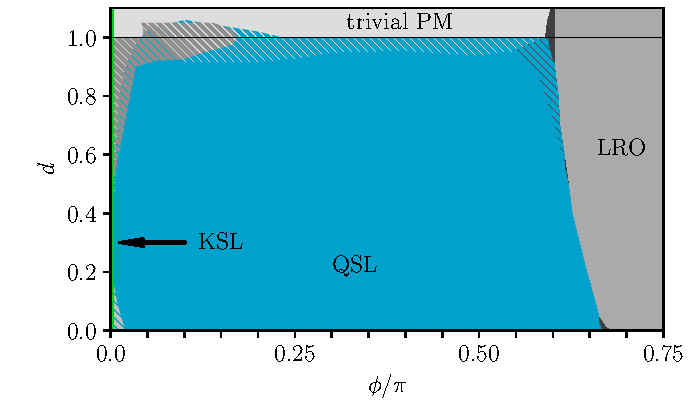
Figure: Schematic phase diagram of the anisotropic K$\Gamma$ model when spatial anisotropy \(d\), as well as \(K = -\cos \phi\) and \(\Gamma = \sin \phi\) are tuned. Hatched patches illustrate regions for which the numerical methods and respective cluster geometries utilized here result in different ground states.
The one-dimensional limit features an emergent Tomonaga-Luttinger liquid (TLL) with the same critical properties as the antiferromagnetic Heisenberg (AFH) chain. Since the TLL is a critical state, most TLLs are unstable under adding small inter-chain coupling. An exception is \emph{sliding Luttinger liquids that occur if the inter-chain coupling competes with the dominant correlations along the chains. As a consequence, long-range order is suppressed. Here, we find that a similar mechanism arises in the strongly anisotropic K\(\Gamma\) model: The TLL phase of the K\(\Gamma\) chain turns into an extended QSL phase. This QSL retains the dominant algebraic correlations along the chains and features spinon-like excitations that are characteristic for the AFH chain. This contrasts the emergent Majorana fermions and \(Z_2\) fluxes of the KSL.
This result is described in the preprint "Extended Quantum Spin Liquid with Spinon-like Excitations in an Anisotropic Kitaev-Gamma Model" Matthias Gohlke, Jose Carlos Pelayo, Takafumi Suzuki, arXiv:2212.11000
3.3 Quantum computers can, sometimes, get what they need
While quantum computers hold great promise, the devices available in the near future will continue to be “noisy, intermediate-scale quantum” (NISQ) platforms, capable of performing only a limited number of quantum operations. For this reason, the development of the quantum computing rests in part on finding algorithms which can run within the limited resources of a NISQ machine.
In an earlier work, [Yunlong Yu et al., Phys. Rev. Research 4, 023249 (2022)] we introduced an alogrithm, the “adaptive-bias Quantum Approximate Optimisation Algorithm” (ab-QAOA), which is capable of solving difficult classical optimization problems with limited quantum resources. In a continuation of this project, we have now extended the ab-QAOA to a canonical hard classical optimization problem, "SAT" or the simultaneous satisfiability of logical clauses.
In collaboration with researchers from Tsinghua University, The Hong Kong University of Science and Technology, and the University of Wisconsion, Madison, we have now shown how the the ab-QAOA is able to solve a class of SAT problems using only resources achievable in a NISQ device. This confirms the ab-QAOA as a quantum algorithm which has the potential to bring a speedup in solving real-world problems.

Figure: Comparison of the resources required to solve a SAT optimisation problem on a quantum computer, using the established Quantum Approximate Optimization Algorithm (QAOA), and the adaptive-bias Quantum Approximate Optimisation Algorithm” (ab-QAOA). The problem considered is Max-1-3-SAT+, for which the QAOA shows a dramatic increase in the resources required ("level p") as the clause density ("α") is increased. In contrast the ab-QAOA is able to solve problems at all clause densities considered, with much lower overhead in resources.
This work is described in the preprint "Solution of SAT Problems with the Adaptive-Bias Quantum Approximate Optimization Algorithm", Yunlong Yu, Chenfeng Cao, Xiang-Bin Wang, Nic Shannon and Robert Joynt, Phys. Rev. Research 5, 023147
3.4 Spurious Symmetry Enhancement and Interaction-Induced Topology in Magnons
From Néel order in the mid 20th century to skyrmion phases in the 21st, magnetically ordered materials have been a constant source of insights into the collective behavior of matter. The coherent spin wave excitations, or magnons, about these magnetic textures provide invaluable information about magnetic structures and couplings. They are also interesting in their own right: as a window into many-body interactions and quasiparticle breakdown, as a platform for investigating band topology, and as an essential ingredient in the functioning of many spintronics devices. One of the most useful theoretical tools at our disposal to understand magnons is an expansion in powers of inverse spin \(S\) based on the Holstein-Primakoff bosonization of quantum spins. The single particle spectrum arising from spin wave theory to lowest order---known as linear spin wave theory (LSWT)---is often used with great success to constrain magnetic couplings from experimental data. This theory is known to fail qualitatively in cases where coupling between single and multi-particle states becomes important such as in highly frustrated magnets and non-collinear spin textures, but also close to quantum phase transitions. Another, more subtle way, in which LSWT can fail qualitatively is called order-by-disorder where spurious ground states and symmetry enhancement exist at the semi-classical level that are lifted by fluctuations. In some instances of quantum order-by-disorder, a spurious continuous symmetry forces the presence of a gapless mode within LSWT where none should be present. In this project, we focus on a related instance of this physics where, instead of failing to capture degeneracy breaking in the ground state, the LSWT instead does not fully capture symmetries that affect degeneracies higher up in the excitation spectrum. The goals of this paper are to spell out ways in which spin wave theory can lead to spurious degeneracies in excitations across the Brillouin zone and to supply a simple, general way to resolve them.
The cases we consider fall into two classes: The first class is where the lattice symmetries are not manifest for exchange couplings between moments out to \(n\)th nearest neighbors but where the symmetries do manifest for longer-range couplings (shell anomaly). The second class is more subtle in that LSWT does not capture certain kinds of exchange anisotropy (anisotropy blindness). Then, LSWT fails to produce the correct magnon spectrum at a qualitative level and spurious symmetry-protected magnon degeneracies occur. We show that degeneracy breaking occurs by carrying out a matrix product state based time evolution (DMRG+tMPO) to resolve band splittings nonperturbatively. While the most straightforward LSWT does not capture the symmetries of the magnetic Hamiltonian, one may show that the symmetry breaking terms, treated perturbatively, lead to effective magnon hopping terms that do resolve spurious degeneracies. This fact leads us to propose a general solution to the problem by including all symmetry-allowed exchange couplings out to some shell.
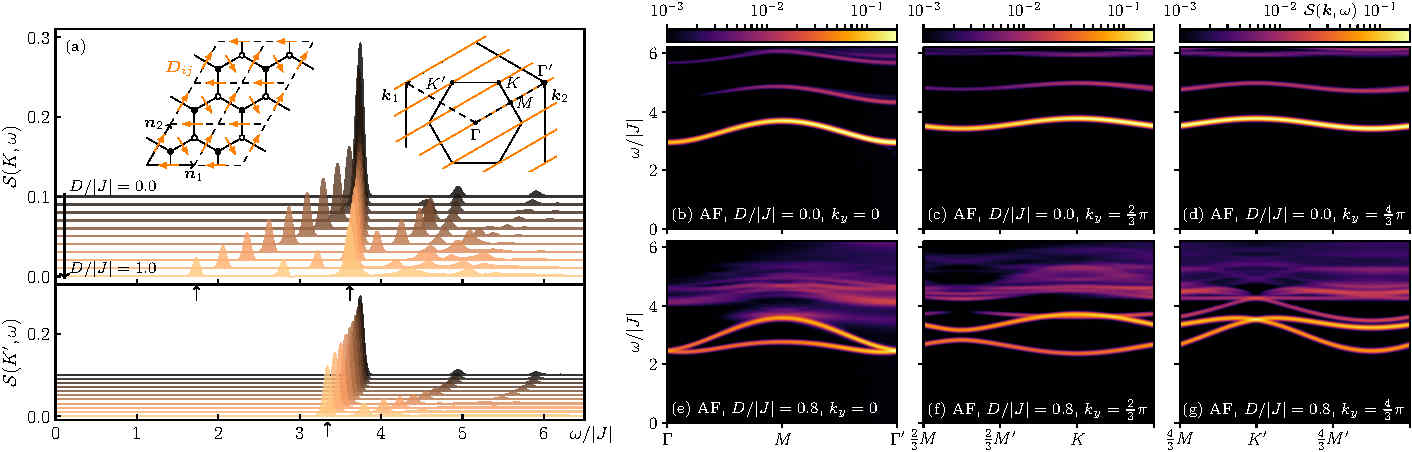
Figure: Non-perturbative calculation of the dynamical spin-structure factor for the spin-\(1/2\) honeycomb lattice antiferromagnet with \(J_z/|J|=2.4\) and Dzyaloshinskii-Moriya interaction (DMI). (a) Line plots at the high-symmetry points \(K\) (top) and \(K'\) (bottom) for increasing DMI from \(D/|J|=0\) to \(D/|J|=1\) illustrate the splitting of the spin-wave bands at \(K\) while the splitting is absent at \(K'\). Magnon bands are highlighted by arrows. (b-g) Representative color plots along momenta cuts (see inset in (a)) for zero (top) and finite DMI (bottom). The magnon bands split across the entire Brillouin zone apart from the \(\Gamma\) and \(K'\) points that feature Dirac cones.
These results are described in the preprint "Spurious Symmetry Enhancement and Interaction-Induced Topology in Magnons" Matthias Gohlke, Alberto Corticelli, Roderich Moessner, Paul A. McClarty, Alexander Mook, Phys. Rev. Lett. 131, 186702
3.5 Quantum paramagnetic states in the spin-1/2 distorted honeycomb-lattice Heisenberg antiferromagnet - application to Cu2(pymca)3(ClO4)
Quantum magnetism has been an essential subject of many investigations through the cooperation of experiments and theory. A spin-1/2 honeycomb-lattice antiferromagnet, Cu2(pymca)3(ClO4), recently joined a family of such subjects. The exciting feature is that the material exhibit gapped paramagnetic behavior down to 2 K, although the simple spin-1/2 honeycomb-lattice antiferromagnetic Heisenberg model exhibits the Neel ordered ground state. The recent X-ray diffraction experiments suggested at least three intralayer exchange interactions in the honeycomb-lattice plane. In our work, we numerically investigated the ground-state properties and dynamics of the extended Honeycomb-lattice antiferromagnetic Heisenberg model with three exchange interactions \(J_A, J_B, J_C\) as a minimal model for the Cu2(pymca)3(ClO4). We remeasured the magnetic susceptibility of its polycrystalline sample with special care and determined the exchange interactions of this material through the comparison with numerical results based on a quantum Monte Carlo method. The obtained interactions revealed that a hexagonal-singlet-type (HS) state could be realized in this material. We also report the ground-state phase diagram and the evolution of the spin gap in the \( J_A/J_C-J_B/J_C\) plane (see the left-hand side figure), which are informative for future and other honeycomb-lattice materials. The characteristic four energy band structures in the HS state in the spin dynamics (see the right-hand side figure) are helpful in clarifying the ground and excited states of Cu2(pymca)3(ClO4) by future neutron scattering measurements.
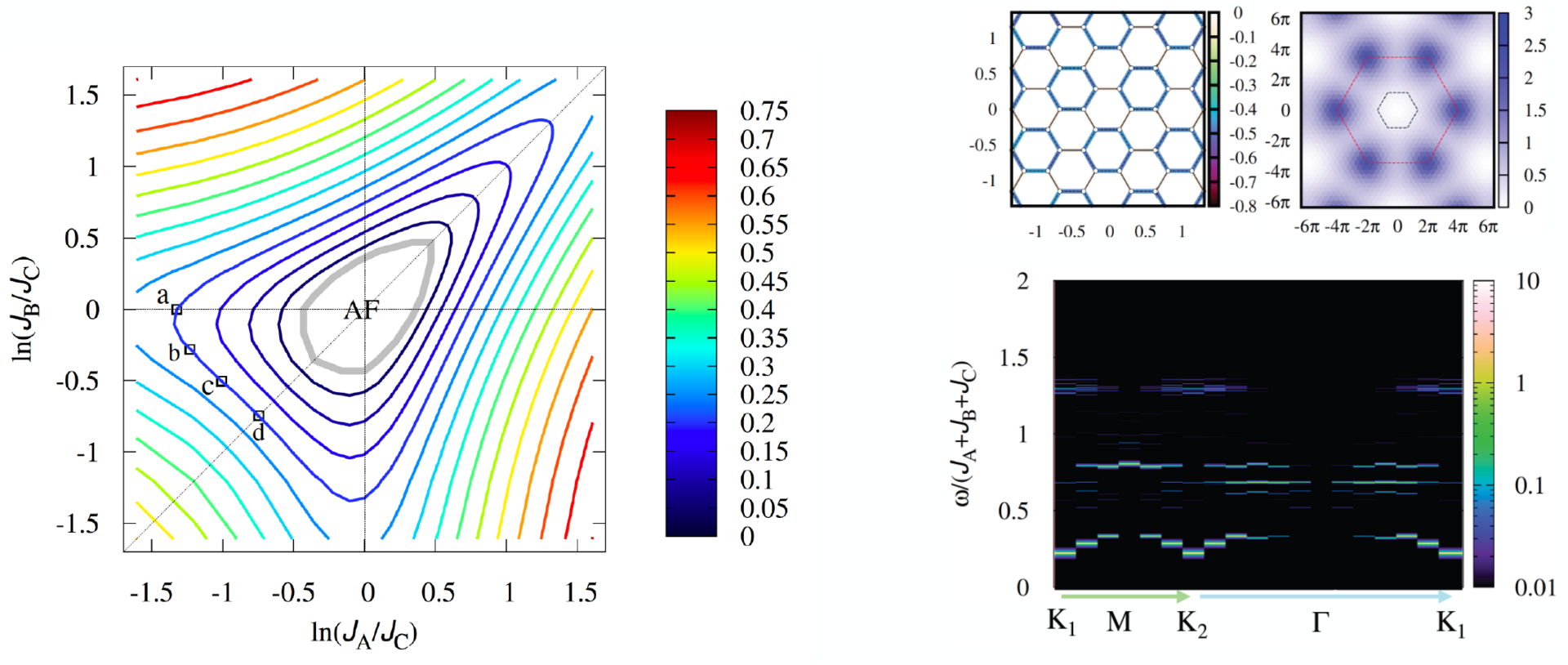
This work was published as: "Quantum paramagnetic states in the spin-1/2distorted honeycomb-lattice Heisenberg antiferromagnet: Application to Cu2 (pymca)3 (ClO4)" Tokuro Shimokawa, Ken'ichi Takano, Zentaro Honda, Akira Okutani and Masayuki Hagiwara, Phys. Rev. B 106, 134410 (2022)
3.6 SUSY Quantum Mechanics on a lattice
The ultimate goal of quantum mechanics is to solve Schrödinger's equation. This equation is postulated to describe the dynamics of quantum mechanical objects. Focusing on a fixed moment in time one can study the time-independent form of this equation which consists of two parts:
One part contains information about a local potential surrounding the object in question the other part contains information about its kinetic energy. This second part usually contains a differential operator of the second order. Starting with Newton and Leibnitz many physicists and mathematicians have developed what is known as differential calculus to solve these problems. To unleash the full power of calculus one must have the underlying space continuous. However, there are some physical systems, for instance the interior of a crystal or nucleus, in which this assumption might not entirely be justified. In these discrete settings, obtaining a solution to Schrödinger's equation without the use of differential calculus becomes much harder.
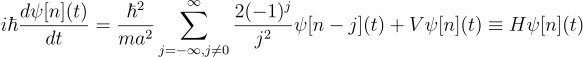
On the other hand, even for the continuous case only a few potentials allow for an exact solution. Interestingly, all these known exact solutions can be obtained by the means of supersymmetric quantum mechanics. In this framework one uses a super potential which factorize the initial potential. Upon the super potential one can define operators that act similarly to the raising and lowering operators known from the algebraic solution of the quantum harmonic oscillator. The algebra of these operators allows for the construction of two partner Hamiltonians whose spectra and eigenfunctions are equivalent up to the ground state. Therefore, solving one of these partner Hamiltonians immediately yields the solution of the other. This procedure can be further generalized and thus one finds the solution of an entire Hierarchy of Hamiltonians [1].
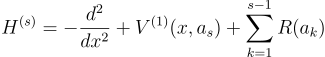
In our work we combined the concept of "Exact discretization", which is a formulation of discrete operators that have many of the desired properties of differential operators recently developed in References [2,3], with the principles of supersymmetric quantum mechanics and suggest a computational procedure allowing to easily solve some lattice problems.
[1] F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry and quantum mechanics,” Phys. Rept. 251, 267-385 (1995)
[2] V. Tarasov, “Exact discretization of Schrödinger equation,” Phys. Lett. A 380, 68-75 (2016)
[3] V. Tarasov, “Exact discretization by Fourier transforms,” Commun. Nonlinear Sci. Numer. Simul. 37, 31-61 (2016)
This work was published as "A Note on Shape Invariant Potentials for Discretized Hamiltonians" Jonas Sonnenschein, Mirian Tsulaia, Modern Physics Letters A Vol. 37, No. 23, 2250153 (2022)
4. Publications
4.1 Journals
- Allen Scheie, Owen Benton, Matthieu Taillefumier, Ludovic D.C. Jaubert, Gabrielle Sala, Niina Jalarvo, Seyed M. Koohpayeh, and Nic Shannon."Dynamical scaling as a signature of multiple phase competition in Yb2Ti2O7" DOI:10.1103/PhysRevLett.129.217202.
- Chenfeng Cao, Yunlong Yu, Zipeng Wu, Nic Shannon, Bei Zeng, Robert Joynt. "Mitigating algorithmic errors in quantum optimization through energy extrapolation" DOI:10.1088/2058-9565/ac969c.
- Tokuro Shimokawa, Ken'ichi Takano, Zentaro Honda, Akira Okutani and Masayuki Hagiwara. "Quantum paramagnetic states in the spin-1/2 distorted honeycomb-lattice Heisenberg antiferromagnet - application to Cu2(pymca)3(ClO4)" DOI:10.1103/PhysRevB.106.134410.
- Jonas Sonnenschein and Mirian Tsulaia. "A Note on Shape Invariant Potentials for Discretized Hamiltonians" DOI:10.1142/S021773232250153X
- Kimberly Remund, Rico Pohle, Yutaka Akagi, Judit Romhanyi and Nic Shannon. "Semi-classical simulation of spin-1 magnets" DOI:10.1103/PhysRevResearch.4.033106
- Yunlong Yu, Chenfeng Cao, Carter Dewey, Xiang-Bin Wang, Nic Shannon, and Robert Joynt. "Quantum Approximate Optimization Algorithm with Adaptive Bias Fields" DOI:10.1103/PhysRevResearch.4.023249
- Hiroshi Ueda, Seiji Yunoki and Tokuro Shimokawa. "Quantum spin solver near saturation: QS3" DOI:10.1016/j.cpc.2022.108369
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
Invited Talks
- Nic Shannon "Negative Thermal Expansion in Cr Spinels" Reconnecting Oxide Research, Edinburgh, UK (2023.03.27)
- Nic Shannon "Observing Magnetic Monopoles in Spin Ice via Electron Holography" MPI-PKS, Dresden, Germany (2023.3.16)
- Nic Shannon "Dynamical Scaling as a Signature of Multiple-phase Competition in Yb2Ti2O7" Clarendon Laboratory, University of Oxford, UK (2023.3.14)
- Nic Shannon "Frustrated quantum spin models: fundamental physics in new placesInterdisciplinary" Science Conference in Okinawa (ISCO 2023): Physics and Mathematics meet Medical Science, OIST (2023.03.02)
- Nic Shannon"Observing Magnetic Monopoles in Spin Ice via Electron Holography" CEMS, RIKEN, Japan (2023.2.15)
- Nic Shannon"Semi-classical simulation of spin-1 magnets" ISSP, The University of Tokyo (2023.2.1)
- Tokuro Shimokawa "Entanglement witnesses in quantum frustrated magnets" Extreme Universe Second Annual Meeting, Kobe Convention Center, International Conference Center (2022.12.27)
- Tokuro Shimokawa "Exact diagonalization for quantum spin systems" (tutorial lecture), APCTP-IACS-SNBNCBS Workshop on Computational Methods for Emergent Quantum Matter:From Theoretical Concepts to Experimental Realization,
S.N. Bose National Center For Basic Sciences, Kolkata & Indian Association for the Cultivation of Science, Kolkata, India (2022.11.22) - Nic Shannon "Rank-2 U(1) spin liquid and q=W order on the breathing pyrochlore lattice: machine-learning assisted solution of a difficult problem in frustrated magnetism" Novel Quantum States in Condensed Matter 2022, Yukawa Institute for Theoretical Physics, Kyoto University (2022.11.29)
- Nic Shannon "From quantum spin liquids to quantum computers" OIST Center for Quantum Technologies Mini-Symposium, OIST, Japan (2022.11.10)
- Tokuro Shimokawa "Entanglement witnesses in quantum frustrated magnets" Extreme Universe Online Kick-Off Meeting of Publicly Offered Research Groups, Online (2022.11.01)
- Nic Shannon "Semi-classical simulation of spin-1 magnets" Quantum Liquid Crystal Meeting, Nagoya, Japan, Hybrid event (2022.09.12)
- Nic Shannon "Semi-classical simulation of spin-1 magnets" Frustrated Metals and Insulators, ICTS, India, Hybrid event (2022.09.14)
- Nic Shannon "Semi-classical simulation of spin-1 magnets" Workshop on Quantum Magnetism, Ascona, Switzerland, Hybrid event (2022.04.27)
Contributed Talks
- Tokuro Shimokawa "Entanglement witnesses for frustrated random singlet state" The Physical Society of Japan 2023 Spring Meeting, Online (2023.03.24)
- Matthias Gohlke "Extended Quantum Spin Liquid with Spinon-like Excitations in an Anisotropic Kitaev-Gamma Model" YIPQS long-term and Nishinomiya-Yukawa memorial workshop Novel Quantum States in Condensed Matter 2022, Yukawa Institute for Theoretical Physics, Kyoto University (2022.11.30)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitations of quantum magnets" DPT2022 German Conference for Women in Physics, Karlsruhe, Germany (2022.11.25)
- Tokuro Shimokawa "Quantum paramagnetic states in the S=1/2 distorted honeycomb-lattice antiferromagnet Cu2(pymca)3(ClO4)" JPS Autumn Meeting 2022, Online (2022.09.12)
- Nic Shannon “Quantum spin liquids and quantum liquid crystals” OIST-Nagoya mini-symposium: “Quantum liquid crystals in localised and itinerant systems”, OIST (2022.07.26)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitations of quantum magnets" OIST-Nagoya mini-symposium: “Quantum liquid crystals in localised and itinerant systems”, OIST (2022.07.26)
- Tokuro Shimokawa "Unbiased numerical studies of the quantum spin liquid/crystal states" OIST-Nagoya mini-symposium: “Quantum liquid crystals in localised and itinerant systems”, OIST (2022.07.26)
- Nic Shannon "Observing Magnetic Monopoles in Spin Ice via Electron Holography" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Online (2022.06.25)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Sorbonne University, Paris, France (2022.06.24)
Seminars
- Nic Shannon "Observing Magnetic Monopoles in Spin Ice via Electron Holography" MPI-PKS, Dresden, Germany (2023.03.16)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism", group of Prof. Frédéric Mila,EPFL Lausanne, Switzerland (2023.03.16)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism", group of Prof. Roser Valenti, Institut für Theoretische Physik Goethe-Universität Frankfurt am Main, Germany (2023.03.13)
- Nic Shannon "Dynamical Scaling as a Signature of Multiple-phase Competition in Yb2Ti2O7" Clarendon Laboratory, University of Oxford, UK (2023.03.14)
- Tokuro Shimokawa "Characterization of quantum frustrated random singlet state via entanglement witnesses" CHS Physics Research Seminar, Nihon University (2023.03.07)
- Leilee Chojnacki "Aspects of gravity in a spin-1 magnet: from a low energy field theory to linearized gravity" Motome group, The University of Tokyo (2023.02.17)
- Nic Shannon "Observing Magnetic Monopoles in Spin Ice via Electron Holography" CEMS, RIKEN, Japan (2023.02.15)
- Nic Shannon "Semi-classical simulation of spin-1 magnets" ISSP, The University of Tokyo (2023.02.01)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism", MPI-PKS, Dresden, Germany,(2023.01.31).
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism", Online Condensed Matter Theory seminars, Online (2022.12.03)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitation of quantum magnets" Valenti group, Institut für Theoretische Physik, Goethe-Universität Frankfurt am Main, Germany (2022.11.22)
- Matthias Gohlke "Quantum Spin Nematics in Square Lattice Frustrated Ferromagnets" The group of Prof. Chisa Hotta, The University of Tokyo (2022.11.10)
- Leilee Chojnacki, "The Universe in a magnetic nutshell: analogue of gravitational waves in a quantum liquid crystal", RAM 2022, OIST (2022.10.20)
Posters
- Tokuro Shimokawa "Characterization of frustrated random singlet state via entanglement witnesses" The 1st young researchers' workshop of the Extreme Universe Collaboration, Graduate School of Mathematics, Nogoya University (2023.02.16)
- Tokuro Shimokawa "Quantum paramagnetic states in the spin-1/2distorted honeycomb-lattice Heisenberg antiferromagnet: Application to Cu2 (pymca)3 (ClO4)" YIPQS long-term and Nishinomiya-Yukawa memorial workshop Novel Quantum States in Condensed Matter 2022, Yukawa Institute for Theoretical Physics, Kyoto University (2022.11.28)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitations of quantum magnets" OIST Center for Quantum Technologies Mini-Symposium, OIST, Japan (2022.11.10)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism" OIST Center for Quantum Technologies Mini-Symposium, OIST, Japan (2022.11.10)
- Kimberly Remund "Spin-1 Magnets - A u(3) Formalism" 29th International Conference on Low Temperature Physics, Sapporo, Japan (2022.08.23)
- Matthias Gohlke "High-field spin-nematic state in the S=1/2 J-K square-lattice frustrated ferromagnet" 29th International Conference on Low Temperature Physics, Sapporo, Japan (2022.08.22)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitations of quantum magnets" 29th International Conference on Low Temperature Physics, Sapporo, Japan (2022.08.20)
- Tokuro Shimokawa "Theory and experiment on the quantum paramagnetic state in the S=1/2 distorted honeycomb-lattice antiferromagnet \(Cu_2(pymca)_3(ClO_4)\)" 29th International Conference on Low Temperature Physics, Sapporo, Japan (2022.08.20)
- Tokuro Shimokawa "High-field exact diagonalization software QS3 and its application to the quantum spin nematic study in the S=1/2 J1-K square-lattice frustrated ferromagnet" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Online (2022.06.28 and 06.30)
- Matthias Gohlke "High-Field Spin-Nematic State in the S=1/2 J-K Square-Lattice Frustrated Ferromagnet" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Sorbonne University, Paris, France (2022.06.22)
- Ananya Samanta "Negative thermal expansion in a magnetically frustrated spinel" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Sorbonne University, Paris, France (2022.06.22)
- Leilee Chojnacki "Analogues of light and gravity in the collective excitations of quantum magnets" The 11th International Conference on Highly Frustrated Magnetism 2022 (HFM22), Sorbonne University, Paris, France (2022.06.21)
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Critical properties of the Anderson transition in random graphs
- Date: March 8, 2023
- Venue: Zoom
- Speaker: Prof. Gabriel Lemarie (CQT-NUS)
6.2 Tensor network approach to Kitaev spin liquid
- Date: March 2, 2023
- Venue: OIST C209 and zoom
- Speaker: Dr. Tsuyoshi Okubo (University of Tokyo)
6.3 Generalizing Tensor Network Methods to Neural Network Wave Functions using Variational Monte Carlo
- Date: February 27, 2023
- Venue: OIST L4E48 zoom
- Speaker: Mr. Douglas Hendry (Northeastern University)
6.4 Skyrmion crystals and their relatives in SU(3) chiral magnetsSkyrmion crystals and their relatives in SU(3) chiral magnets
- Date: February 14, 2023
- Venue: OIST L4F01 and zoom
- Speaker: Dr. Yuki Amari (University of Tokyo)
6.5 Spin nematic, dimensional reduction, and chiral spin liquid in the spin-1 Kitaev-Heisenberg model with biquadratic interactions
- Date: January 17, 2023
- Venue: OIST B503 and zoom
- Speaker: Dr. Rico Pohle (University of Tokyo)
6.6 Evidence for a hidden order in the pyrochlore iridate Nd2Ir2O7
- Date: October 26, 2022
- Venue: OIST C700 and zoom
- Speaker: Dr. B.J. Kim (Postech, Korea)
6.7 Exploring Quantum Phases of Matter on Quantum Processors
- Date: October 25, 2022
- Venue: Zoom
- Speaker: Dr. Frank Pollmann (Technische Universität München)
6.8 Probing triangular-lattice quantum spin liquids with LF-μSR
- Date: October 11, 2022
- Venue: Zoom
- Speaker: Dr. Francis Pratt (ISIS Neutron and Muon Source, STFC-RAL, Didcot UK)
6.9 Contemporary approaches to variational quantum algorithms for quantum chemistry
- Date: October 4, 2022
- Venue: OIST L4E01 and zoom
- Speaker: Dr. Andreas Thomasen (QunaSys)
6.10 Searching for hidden phases born of a quantum spin liquid
- Date: September 21, 2022
- Venue: OIST L4E48 and zoom
- Speaker: Mr. Hyeok-Jun Yang (KAIST)
6.11 Classification of classical spin liquid in the large-S limit
- Date: August 17, 2022
- Venue: OIST C700
- Speaker: Dr. Han Yan (Rice University)
6.12 Itinerant frustration in van der Waals coupled iodides
- Date: August 2, 2022
- Venue: Zoom
- Speaker: Dr. Ryutaro Okuma (University of Oxford)
6.13 On spins and neurons: investigating brain function with Ising models and renormalization group inspired approaches
- Date: July 12, 2022
- Venue: OIST C700 and zoom
- Speaker: Dr. Leenoy Meshulam (University of Washington)
6.14 Probing spinons by Electron Spin Resonance: hidden interactions in a spin chain
- Date: July 5, 2022
- Venue: Zoom
- Speaker: Dr. Kirill Povarov (Laboratory for Solid State Physics, ETH Zurich)
6.15 Quantum distance and flat band
- Date: June 28, 2022
- Venue: Zoom
- Speaker: Prof. Jun Won Rhim (Ajou University, Korea)
6.16 Diagnosing weakly first-order phase transitions by coupling to order parameters
- Date: June 14, 2022
- Venue: Zoom
- Speaker: Prof. Andreas Läuchli (Paul Scherrer Institute / EPFL)
6.17 The Majorana-Hubbard Model
- Date: June 7, 2022
- Venue: Zoom
- Speaker: Prof. Ian Affleck (The University of British Columbia)
6.18 Projective symmetry group classification of chiral Z_2 spin liquids on the pyrochlore lattice: Application to the XXZ model
- Date: May 24, 2022
- Venue: Zoom
- Speaker: Mr. Benedikt Schneider (Ludwig Maximilian University Munich)
6.19 Tensor network renormalization study on the crossover in classical Heisenberg and RP2 models in two dimensions
- Date: May 17, 2022
- Venue: Zoom
- Speaker: Dr. Atsushi Ueda (University of Tokyo)
6.20 Disorder in the Kitaev spin liquid
- Date: May 10, 2022
- Venue: Zoom
- Speaker: Prof. Natalia Perkins (University of Minnesota)
6.21 Duality, Criticality, Anomaly, and Topology in Quantum Spin-1 Chains
- Date: April 22, 2022
- Venue: OIST C209
- Speaker: Mr. Hong Yang (University of Tokyo)
6.22 Exotic QLC states in Fe-based superconductors, kagome metals, and twisted bilayer graphene
- Date: April 19, 2022
- Venue: Zoom
- Speaker: Prof. Hiroshi Kontani (University of Tokyo)
7. Other
Nothing to report.



