FY2016 Annual Report
Theory of Quantum Matter Unit
Professor Nic Shannon

Abstract
FY2016 was another busy year, in which the Unit successfully completed its first "Unit Review". In June 2016, a distinguished panel of international experts visited OIST, and spent 2 days with the TQM Unit members, before writing a report on what had been accomplished by the Unit over the last 4 years.
The TQM Unit was sad to say goodbye to its Group Leader, Ludovic Jaubert, who left to take up a CNRS CR1 Position in Bordeaux, France, and Owen Benton, who moved onto a posdoc in RIKEN. However the Unit was happy welcome two new postdocs : Judit Romhanyi arrived from the Max Planck Institute for Solid State Physics, Stuttgart, while Tokoru Shimokawa moved to OIST from Osaka University. The Unit also welcomed a JSPS Fellow, Yurika Kubo, from Waseda University; a Research Intern, Victor Drouin-Touchette; and was happy to see the return of Kimberly Remund, who successfully defended a MSc Thesis at EPFL, Switzerland, based on work carried out as an Intern in the TQM Unit.
The Unit continued to be very active in research on on frustrated magnets, publishing papers on topics ranging from a new form spin liquid resembling linearised General Relativity, to the quantum origins of moment fragmentation.
The Unit was also also active in promoting its work, giving a total of 48 presentations, including 26 invited talks, at a wide range of research institutions, workshops and conferences. In September 2016 the entire TQM Unit attended the conference "Highly Frustrated Magnetism 2016" (HFM 2016) in Taipei, Taiwan, where several Unit members were invited or selected to give talks. Several present and former members of the Unit also gave talks at "Statistical Physics 2016", in Lyon, France.
The Unit continued its tradition of outreach activity, with Ludovic Jaubert, Karim Essafi and Rico Pohle staging a hands-on introduction to superconductivity for students attending the 2016 OIST Science Challenge, while work on new spin liquids and moment fragmentation was reported in press releases picked up by a wide range of international media.
1. Staff
- Prof. Nic Shannon, Professor
- Dr Ludovic Jaubert, Group Leader ( - Jan 2017)
- Dr John Owen Benton, Postdoctoral Scholar ( - Sep 2016)
- Dr Karim Essafi, Postdoctoral Scholar
- Dr Judit Romhanyi, Postdoctoral Scholar
- Dr Tokuro Shimokawa, Postdoctoral Scholar
- Dr Mathieu Taillefumier, Postdoctoral Scholar
- Ms Yurika Kubo, JSPS Fellow
- Ms Christina Lee, PhD Student
- Mr. Rico Pohle, PhD Student
- Mr. Han Yan, PhD Student
- Ms Victor Drouin-Touchette, Research Intern
- Ms. Kimberly Remund, Research Intern
- Ms. Shiho Saito, Research Administrator
2. Collaborations
- Theme: Quantum Spin Ice
- Researchers:
- Prof. Ying Jer Kao, National Taiwan University
- Prof. Karlo Penc, Budapest
- Prof. Frank Pollmann, TUM
- Dr Olga Sikora, Jagiellonian University
- Prof. Nic Shannon, OIST
- Researchers:
- Theme: Exotic Unconventional magnetic phases in BaCdVO(PO4)2
- Researchers:
- Dr Yurika Kubo, OIST
- Dr Burkhard Schmidt, MPI-CPfS
- Prof. Nic Shannon, OIST
- Dr Markos Skoulatos, TUM
- Dr Andrew Smerald, EPFL
- Researchers:
- Theme: Semiclassical dynamics of quantum spin ice
- Researchers:
- Dr Owen Benton, RIKEN
- Dr Ludovic Jaubert, CNRS
- Prof. Nic Shannon, OIST
- Dr Mathieu Taillefumier, OIST
- Researchers:
- Theme: Topological Excitations in Frustrated Magnets
- Researchers:
- Dr Yutaka Akagi, University of Tokyo
- Prof. Nic Shannon, OIST
- Dr Hiroaki Ueda, Toyama Prefectural University
- Researchers:
- Theme: Breathing asymmetry in pyrochlore and kagome lattices
- Researchers:
- Dr Karim Essafi, OIST
- Dr Ludovic Jaubert, OIST
- Prof. Masafumi Udagawa, Gakushuin University
- Researchers:
- Theme: Fully Anisotropic model on the kagome lattice
- Researchers:
- Dr Karim Essafi, OIST
- Dr Ludovic Jaubert, OIST
- Dr Owen Benton, RIKEN
- Researchers:
- Theme: Spin liquids of topological charges
- Researchers:
- Dr Tomonari Mizoguchi, University of Tokyo
- Dr Ludovic Jaubert, OIST
- Prof. Masafumi Udagawa, Gakushuin University
- Researchers:
- Theme: Classical spin liquids in stacked triangular lattices
- Researchers:
- Dillon Liu, Oxford University, UK
- Dr Ludovic Jaubert, OIST
- Prof. Fiona Burnell, University of Minnesota, USA
- Prof. John Chalker, University of Oxford, UK
- Researchers:
- Theme: Thin film of spin ice
- Researchers:
- Dr Ludovic Jaubert, OIST
- Dr Taoran Lin, University of Waterloo, Canada
- Ms. Tuba Opel, University of Waterloo, Canada
- Prof. Peter Holdsworth, ENS Lyon, France
- Prof. Michel Gingras, University of Waterloo / Perimeter Institute, Canada
- Researchers:
- Theme: Unquenched orbitals and frustration
- Researchers:
- Dr Judit Romhányi, OIST
- Prof. Leon Balents, Kavli Institute, UCSB, USA
- Dr George Jackeli, Max Planck, Germany
- Researchers:
- Theme: Quandrupole Excitations in 2d Quantum Magnet
- Researchers:
- Dr Mitsuru Akaki, Osaka University, Japan
- Dr Daichi Yoshizawa, Osaka University, Japan
- Akira Okutani, Osaka University, Japan
- Dr Takanori Kida, Osaka University, Japan
- Dr Judit Romhányi, OIST
- Prof. Karlo Penc, Wigner Research Centre for Physics, Hungary
- Prof. Masayuki Hagiwara, Osaka University, Japan
- Researchers:
- Theme: Curie-law Crossover: An easy-to-measure signature of spin liquids
- Researchers:
- Rico Pohle, OIST
- Dr Ludovic Jaubert, CNRS, Bordeaux University
- Researchers:
- Theme: Symmetry and Optical Selection Rules in Graphene Quantum Dots
- Researchers:
- Rico Pohle, OIST
- Dr Eleftheria G. Kavousanaki, OIST & University of Crete, Greece
- Prof. Keshav M. Dani, OIST
- Prof. Nic Shannon, OIST
- Researchers:
3. Activities and Findings
3.1 Classical spin liquids in stacked triangular antiferromagnets
The triangular-lattice Ising antiferromagnet is arguably the simplest model of a classical spin liquid. A group of researchers based in the University of Oxford, the University of Minnesota and the TQM Unit have decided to explore a three-dimensional version of this canonical model, built from stacked triangular layers with frustrated interlayer interactions (abc and abab stacking).
Their study is motivated in part by observations of charge ordering in the materials LuFe2O4 and YbFe2O4. The charge states of Fe2+ and Fe3+ ions in these systems can be represented using Ising pseudospins, with antiferromagnetic coupling between pseudospins arising from screened Coulomb interactions. The pseudospins occupy the sites of an abc-stacked triangular lattice, though with an alternating layer spacing that is not included in the models under study. Experimental studies, in particular of YbFe2O4, find helices of scattering intensity in a temperature range above a three-dimensional charge-ordering transition.
While an accurate description of these materials would require treating additional (magnetic) degrees of freedom, the group of researchers have found that strong interlayer correlations can indeed arise over an extended temperature range without long-range order. Indeed, if interlayer couplings are much weaker than in-plane ones, the paramagnetic phase of models with frustrated stackings has a classical spin-liquid regime at low temperature, in which correlations are strong both within and between planes, but in absence of long-range order. By contrast, for the unfrustrated (aaa) stacking, there is no extended regime in which interlayer correlations are strong without three-dimensional order.
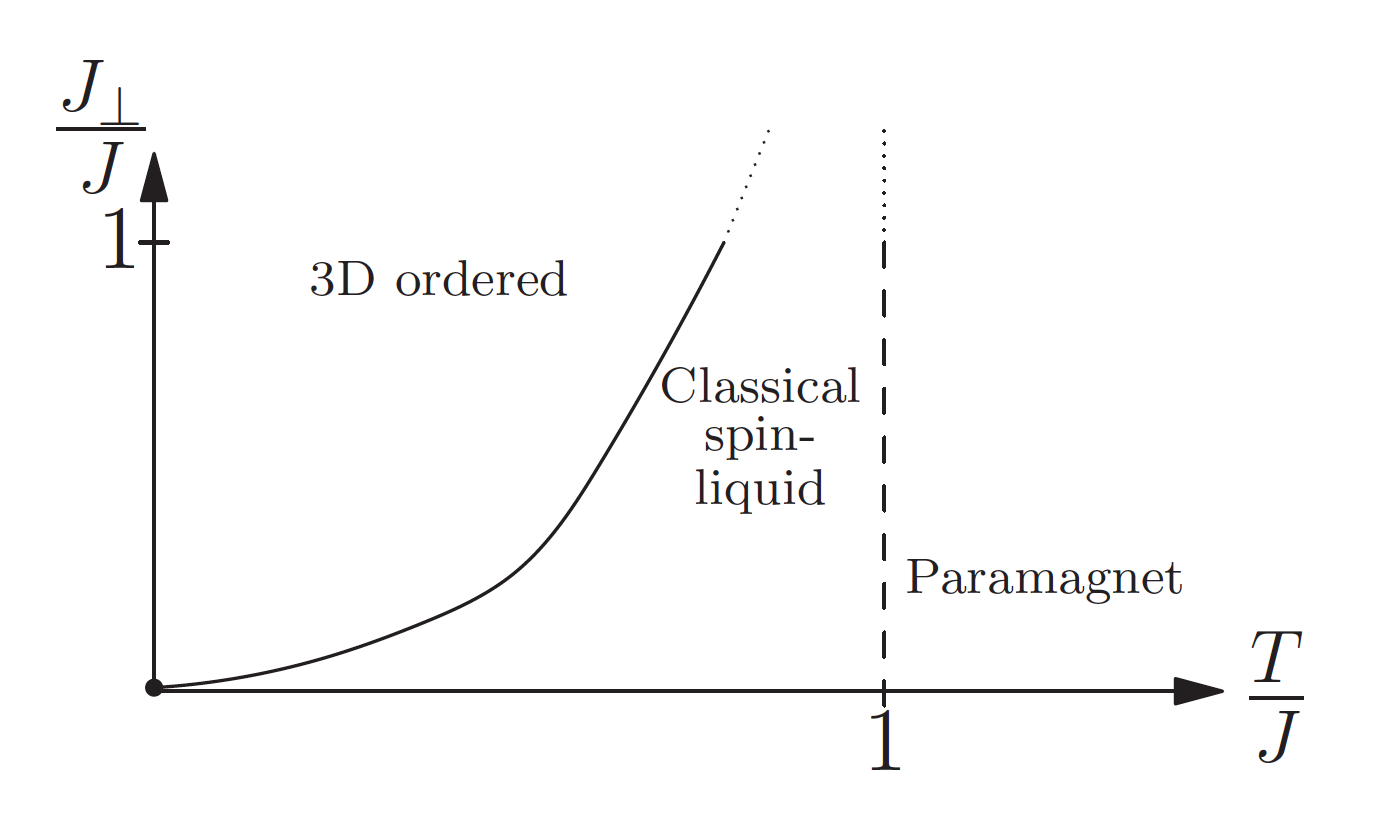
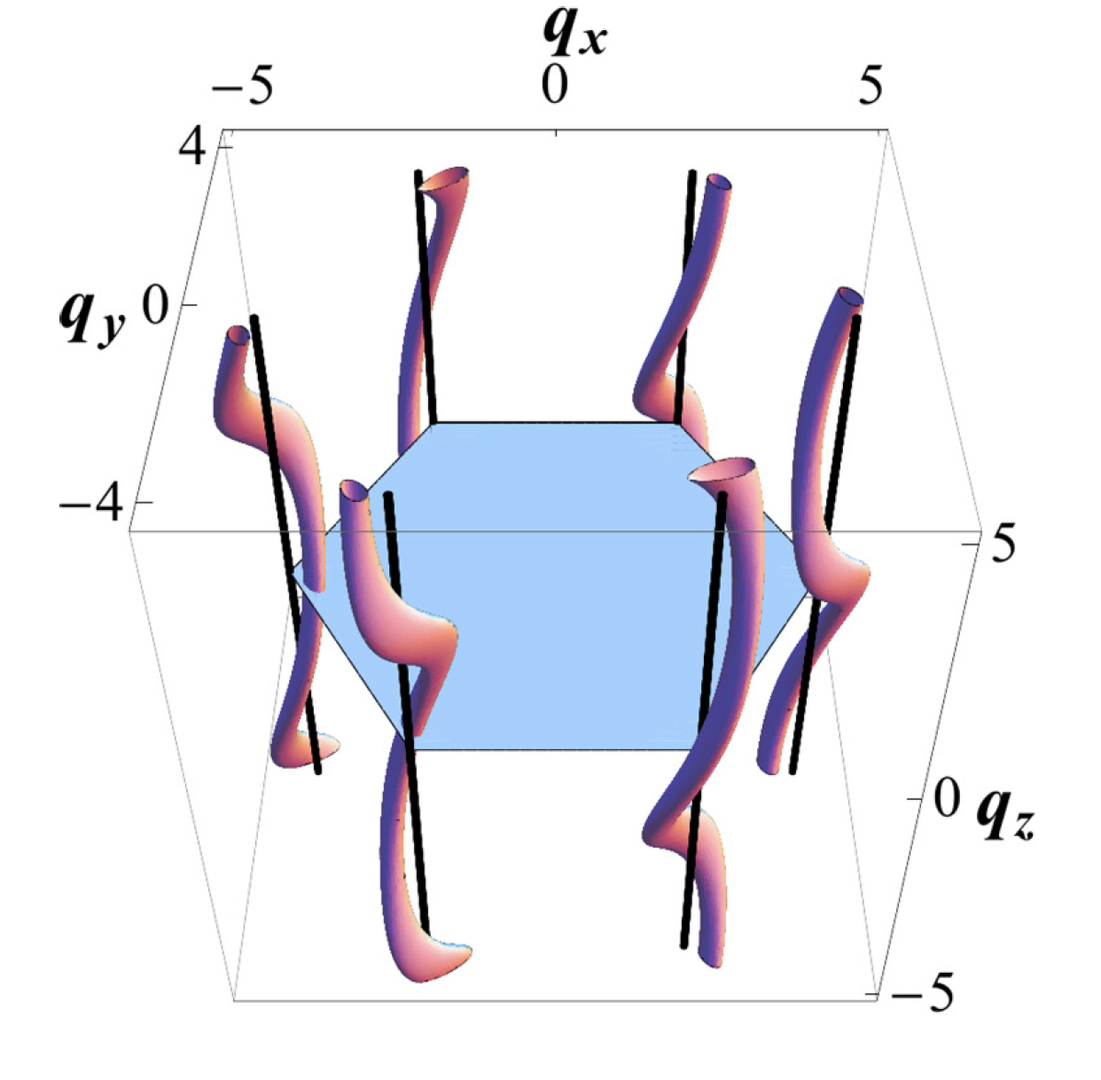
Figure 3.1: Left: Schematic phase diagram for stacked triangular-lattice Ising antiferromagnets. Right: Maxima in the structure factor form helices in the three-dimensional reciprocal space.
This work was published as "Classical spin liquids in stacked triangular lattice Ising antiferromagnets" D. T. Liu, F. J. Burnell, L. D. C. Jaubert, and J. T. Chalker. Phys. Rev. B 94, 224413 (2016)
3.2 Thin films of spin ice: surface ordering of magnetic charges
Highly frustrated magnets host an impressive array of exotic many-body phenomena, taking us far from the conventional paradigms of collective magnetic behavior. The formulation of the local frustrated constraints in terms of gauge fields has revolutionized our perspective on these systems. As exposed in classic textbooks on electromagnetism, boundaries dramatically influence the behavior of gauge fields. This is how Ludovic from the TQM Unit, together with Taoran Lin, Tuba Opel and Michel Gingras from Waterloo (Canada) and Peter Holdsworth from Lyon (France) have been led to wonder what may be the role of boundary conditions in frustrated magnets described by gauge theories.
Classical spin ice presents itself as a nascent paragon to lay the foundations of such concepts, motivated by recent realizations of Dy2Ti2O7 and Ho2Ti2O7 spin ice thin films. The resulting open boundaries make half of the bonds on the interfaces inequivalent. By tuning the strength of these inequivalent "orphan" bonds, dipolar interactions induce a surface ordering equivalent to a two-dimensional crystallization of magnetic surface charges. This surface ordering may also be expected on the surfaces of bulk crystals. For ultrathin films made of one cubic unit cell, once the surfaces have ordered, a square ice phase is stabilized over a finite temperature window. The square ice degeneracy is lifted at lower temperature and the system orders in analogy with the well-known F-transition of the 6-vertex model.
If the lattice parameters of the substrate are incommensurate with those of the spin-ice film, lattice distortions are invariably induced on the surface which can penetrate into the film, inducing a “bond distortion field”. In experiments on Dy2Ti2O7 films, such a a substrate-induced strain has been identified as a possible mechanism for the loss of residual Pauling entropy compared to bulk samples. In the present work, Monte Carlo simulations qualitatively confirm that strain can lead to a smooth loss of Pauling entropy.
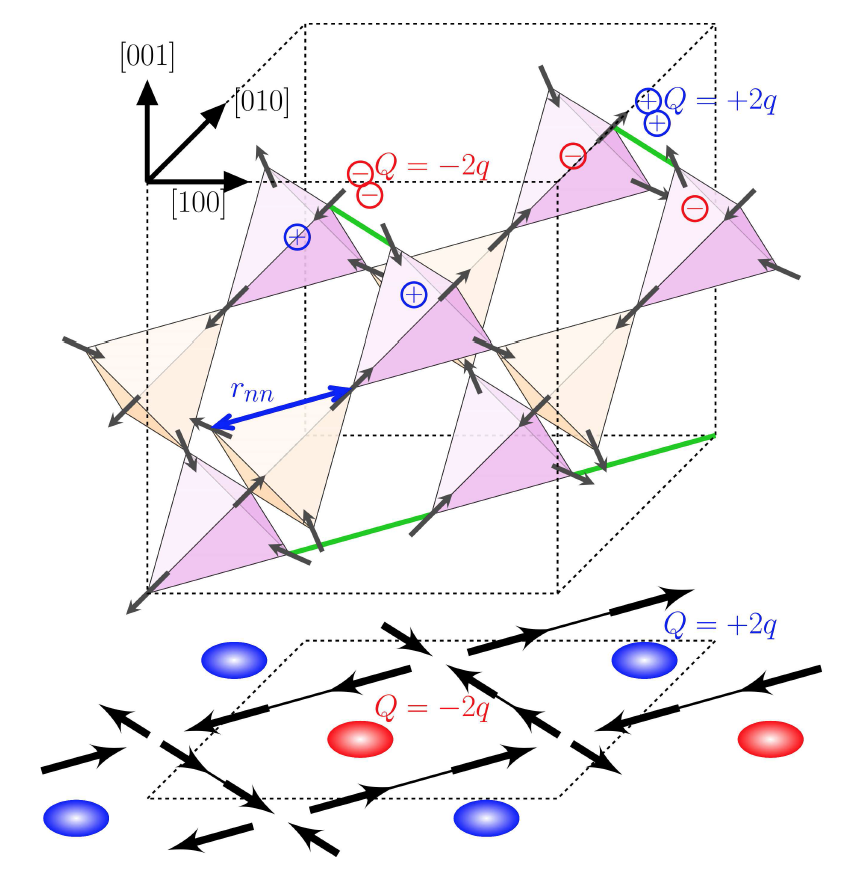
Figure 3.2: Spin ice thin film cleaved in the [001] direction. Open boundaries lead to orphan bonds (green) on the surfaces playing the role of a local chemical potential for effective magnetic charges on the surfaces. Below the surface ordering temperature, the central tetrahedra (orange) develop into a square ice phase, as seen by the projection of the spins in plane.
This work was published as "Spin Ice Thin Film: Surface Ordering, Emergent Square Ice, and Strain Effects" L. D. C. Jaubert, T. Lin, T. S. Opel, P. C. W. Holdsworth, and M. J. P. Gingras. Phys. Rev. Lett. 118, 207206 (2017)
3.3 Clustering of Topological Charges in Kagome Classical Spin Liquid
Fractionalization is a hallmark of topological states of matter. In these systems, an excitation with a unit quantum number, such as charge and spin, is fractionalized into several constituents. These excitations can then condense into exotic topological phases. In the TQM Unit, Ludovic has collaborated with Tomonari Mizoguchi (Tokyo University) and Masafumi Udagawa (Gakushuin University) in order to investigate the collective behavior of fractionalized topological charges in the J1-J2-J3 Ising model on the kagome lattice.
When J2 = J3, this model can be mapped onto a model of interacting charges constrained by Gauss’ law. The attraction/repulsion between these charges is now tunable, and their recombination gives rise to a yet unexplored classical spin liquid. This spin liquid is characterized by an extensive residual entropy, as well as a fully packed phase of clusters of same-sign topological charges. These clusters are usually centered around a closed hexamer of triangles out of which open branches proliferate. The emergence of hexamers is reflected to a half-moon pattern in the magnetic structure factor, which provides us a signature of this spin liquid in neutron-scattering experiments. As a side benefit, the study of this spin liquid has necessitated the development of a worm algorithm which does not require the presence of a local conservation law, as opposed to traditional Coulomb-phase physics.
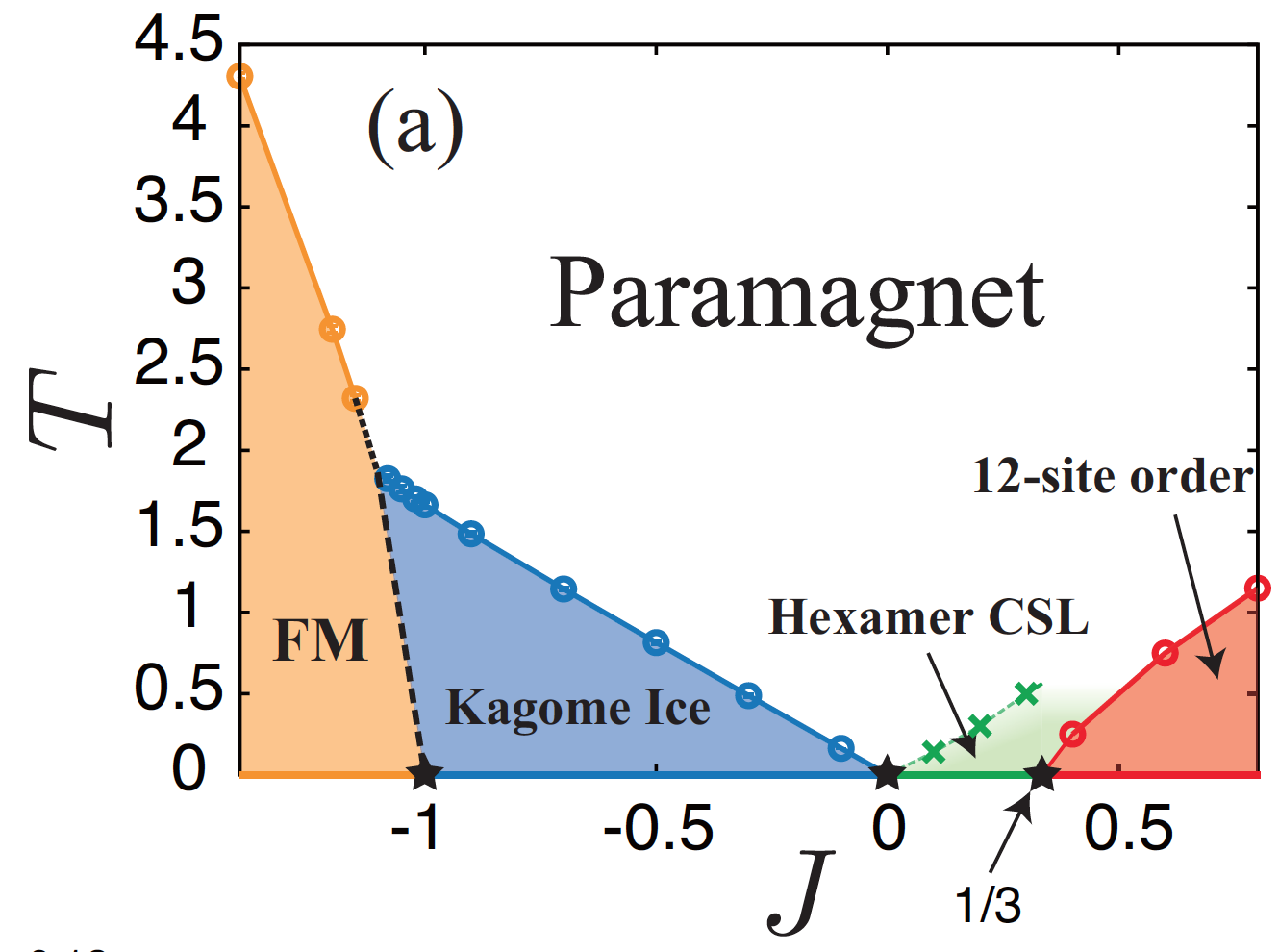
Figure 3.3: Phase diagram for attractive (J<0) and repulsive (J>0) interaction between charges of opposite sign. Open circles are phase transitions, while crosses are crossovers; there is no long-range order in the kexamer classical spin liquid (green).
This work was published as "Clustering of Topological Charges in Kagome Classical Spin Liquid", T. Mizoguchi, L. D. C. Jaubert and M. Udagawa Phys. Rev. Lett. 119, 077207 (2017)
3.4 Symmetry and optical selection rules in graphene quantum dots
The discovery of Graphene, more than 10 years ago, has sparked a renaissance in the study of two-dimensional materials and their potential technological applications. Graphene quantum dots (GQD's) bring another new opportunity with potential applications in fields ranging from quantum computation to solar energy. However, in order to tailor the properties of a GQD to a specific purpose it is vital to understand the relationship between the size and shape of the dot and its physical properties.
In collaboration between the Theory of Quantum Matter Unit and the Femtosecond Spectroscopy Unit of OIST Mr. Rico Pohle, Dr Eleftheria Kavousanaki, Prof. Keshav Dani and Prof. Nic Shannon explored the role that size, shape, edge-type and atomic vacancies play in the optical response of GQD's. Using group theory, they could reveal optical selection rules which follow from the symmetry of a regular shaped GQD, identifying the different roles played by linear and circularly-polarised light in different GQD's with different shape. The study of the optical conductivity σ(ω) of GQD's within a simple tight-binding model showed that for GQD's of intermediate size (≈ 10nm), σ(ω) is sensitive to the edge-type of the dot, with the presence of zigzag edges heralded by a new peak in σ(ω) at the UV end of the visible spectrum (see Fig. 3.4). States causing this peak were identified to be 1-dimensional, providing a natural explanation for large binding energies of the associated excitons in bulk graphene. Shape-asymmetry and atomic vacancies in the optical response of GQD's can be used to even enhance the number of these states. Since GQD's with both regular and irregular shapes are now available we hope that this article will stimulate further experimental work on this topic.
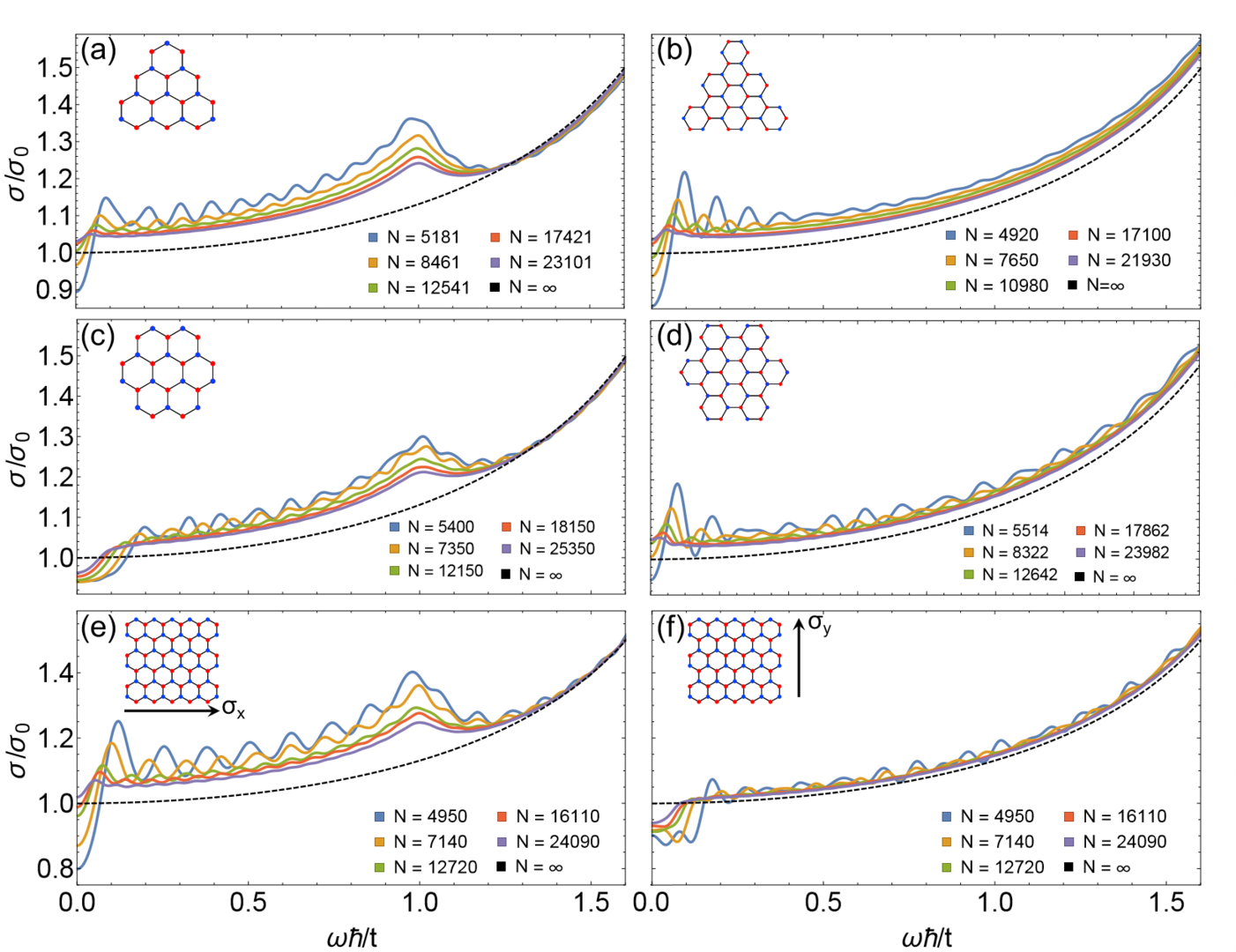
Figure 3.4: Low frequency part of the optical conductivity σ(ω). (a) Triangular zigzag, (b) triangular armchair, (c) hexagonal zigzag, (d) hexagonal armchair, (e)--(f) rectangular graphene quantum dot for both x- and y- polarized light, for sizes up to N ≈ 25,000. The peak at σ/t = 1 in σ(ω) for dots with zigzag edges (polarization parallel to the zigzag edge) is distinguishable from the featureless conductivity of dots with armchair edges. We compare the results to the analytical solution for a graphene sheet in its thermodynamic limit (dashed line).
This work was published as "Symmetry and optical selection rules in graphene quantum dots" R. Pohle, E. G. Kavousanaki, K. M. Dani, and N. Shannon. Phys. Rev. B 97, 115404 (2018)
3.5 Flat Bands and Dirac Cones in Breathing Lattices
The pyrochlore and Kagome lattices are paragons of magnetic frustration, where anisotropy is the name of the game. Anisotropy can take several forms: single ion, bond or lattice anisotropy for example. The latter form naturally appears in breathing lattices, where interactions on neighbouring units (triangles or tetrahedra) are free to differ, from ferromagnetic to antiferromagnetic. Motivated by the recently synthesized breathing materials such as rare-earth pyrochlore Ba3Yb2Zn5O11, vanadium oxyfluoride kagome[NH4]2[C7H14N][V7O6F18] and spinel oxides LiInCr4O8 and LiGaCr4O8; Dr Karim Essafi and Dr Ludovic Jaubert in collaboration with Prof. Masafumi Udagawa (Gakushuin University, Tokyo) have explored how lattice anisotropy modifies the mode spectrum of kagome and pyrochlore lattices with classical Heisenberg spins.
They have shown that the nature and degeneracy of the flat bands is preserved for any value of the anisotropy. These flat bands can coexist with Dirac nodes at the Γ point when the model becomes particle-hole symmetric. Moreover, the ground-state for the breathing kagome lattice, breaks the time-reversal symmetry of the Hamiltonian to support a spontaneous chirality when neighbouring triangles are alternatively ferromagnetic and antiferromagnetic.

Figure 3.5: When the model becomes particle-hole symmetric, a Dirac cone appears in the mode spectrum of the breathing kagome (left) and pyrochlore (middle) lattices. In this region, the breathing kagome ground state displays a spontaneous chirality (right).
This work was published as ”Flat bands and Dirac cones in breathing lattices” K. Essafi, L.D.C Jaubert and M. Udagawa J. Phys.: Condens. Matter 29 (2017) 315802 (Accepted for publication in JPCM).
3.6 Unquenched orbitals and frustration
Conventionally, frustration, low dimensionality and low spin are the key attributes of emerging novel quantum ground states. In the quest to realize quantum spin liquid states characterized with massive entanglement and the lack of magnetic order, researchers have extensively studied Mott insulators with antiferromagnetic interactions on geometrically frustrated lattices.
Alternatively, unquenched angular momentum and orbital degrees of freedom may open a route to frustration. The directional character of degenerate d-orbitals may frustrate the magnetic interactions even on bipartite lattices, and lead to a plethora of emergent phases lacking long-range spin/orbital order.
Dr Judit Romhányi in collaboartion with Prof. Leon Balents (Kavli Institute for Theoretical Physics) and Dr George Jackeli (Max Planck) study a spin-orbital model suitable for a family of d1 cubic double perovskites. Variational and analytical approaches reveal a rich phase diagram emerging from the interplay of Hund’s coupling and spin-orbit interaction. We show that a dimer-singlet phase, corresponding to a random arrangement of spin-orbital singlets is a natural ground state for a parameter set relevant for the molybdenum compound, Ba2YMoO6.
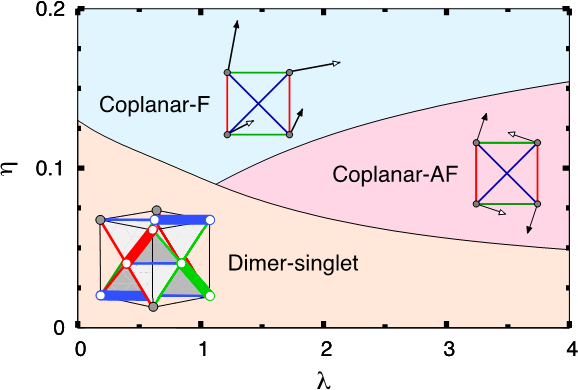
Figure 3.6: Phase diagram as function of spin-orbit (lambda) and Hund’s (eta) couplings. For small values of eta the dimer-singlet phase is stable in the entire range of lambda. Increasing eta, non-collinear coplanar ordered phases emerge.
The dimer-singlet phase does not exhibit any long-range order, nor breaks any global symmetries. Its extensive degeneracy explains the observed glassy behavior and residual entropy. Neutron scattering experiments on powder samples revealed excitations that are in line with the spectrum of weakly coupled spin-orbit dimers. An intense mode is interpreted in our work as a spin singlet-to-triplet excitation. A less intense, lower-energy response is naturally attributed to orbital excitation.
In addition, our model supports complex, non-collinear, coplanar ordered patterns, relevant for the osmium compounds.
Constructing a minimal microscopic model, we uncover the physical origin of the unusual amorphous valence bond state experimentally suggested for Ba2BMoO6 (B=Y,Lu), and predict possible ordered patterns for the Ba2BOsO6 (B=Na,Li) compounds.
This work was published as ”Spin-Orbit Dimers and Non-Collinear Phases in d1 Cubic Double Perovskites” J. Romhányi, L. Balents and G. Jackeli. Phys. Rev. Lett. 118, 217202 (2017)
3.7 Quadrupole excitations in 2d quantum magnets
Multipole – nematic, quadrupole, and octupole – ordering in quantum magnets have long been proposed theoretically, inspiring the quest to find them in experiments. However, when relying on standard experimental methods, such phases usually remain 'hidden'.
Similarly, reports of experimental observation of multipolar fluctuations of spins are unparalleled in the literature.
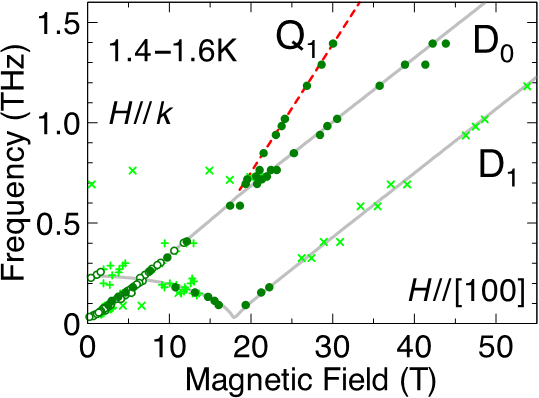
Figure 3.7a: ESR spectrum of Sr2CoGe2O7. Open circles (plus) are strong (weak) resonance signals obtained from the measurements in static fields at 1.6 K, while solid circles (cross) show strong (weak) resonance signals in pulsed fields at 1.4 K. Solid lines represent the modes from the multiboson spin- wave theory. Dashed line indicates the resonance mode with a slope twice larger than the others, corresponding to a two-magnon excitation.
We report the first unambiguous experimental observation of a spin multipolar excitations. We study single crystals of multiferroic Sr2CoGe2O7, and show that due to its nearly isotropic nature a purely quadrupolar bimagnon mode appears in the electron spin resonance spectrum. On the account of magneto-electric coupling present in the Sr2CoGe2O7, this non-magnetic spin-excitation couples to the electric field of the light and becomes observable for a specific experimental configuration, in full agreement with a theoretical analysis of the selection rules.
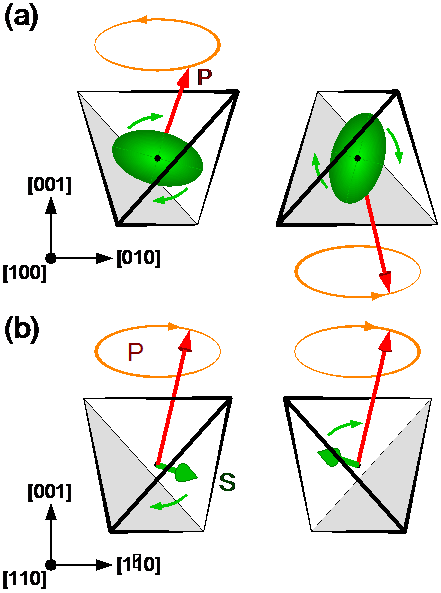
Figure 3.7b: Schematic figure of (a) quadrupolar mode Q1 for H∥[100] and (b) dipolar wave D1 for H∥[110], as seen from the direction of the magnetic field. The green ellipse represents the rotating quadrupolar moments, while the green arrows the precessing dipolar spin. The red arrows show the electric polarization vector.
The features of the experimental spectra taken in different geometries are explained by a simple theoretical model of this spin-quadrupolar wave providing not only a qualitative description, but also a quantitative agreement. The physical picture considered here may apply to a broad family of magnetic multiferroic materials. Studying dynamical properties can help discovering hidden orders, and is of fundamental importance for applications and materials research.
This work was published as ”Direct observation of spin-quadrupolar excitations in Sr2CoGe2O7 by high field ESR” M. Akaki, D. Yoshizawa, A. Okutani, T. Kida, J. Romhányi, K. Penc and M. Hagiwara Phys. Rev. B 96, 214406 (2017)
3.8 Hidden quadrupolar order and monopoles fate in quantum spin ices
Ising ices are probably the most famous example of frustrated magnets in which the magnetic states are disordered but still show correlations over large distance. Quantum spin ices are their quantum counterparts but are much less understood than their classical cousins.
Exact diagonalization is limited in size while Montecarlo methods suffer from the infamous sign problem which limit the study of quantum spin ice to a limited range of the parameters space.
Like many quantum spin models, it is possible to study them in the classical limit and study the different classical phases using classical Montecarlo methods while their excitations are also accessible with molecular dynamis methods. In a set of two papers in preparation, we studied the thermodynamics and the semi-classical dynamics over the full range of the parameters sets defining the quantum spin ices.
The full phase diagram, depicted on Fig.1 is extremely rich with a variety of different spin liquids including the classical spin ices, an ordered antiferromagnetic phase for Jx00B1 with reentrant behavior and a magnetic phase showing no dipolar order but quadrupolar order.
The semi-classical dymamics of quantum spin ices model is as subtle as its classical thermodynamics. The dynamical structure factor of the spin liquid with hidden quadrupolar order has a broad continuum of excitations which is an indication of absence of conventional magnetic order while calculations of the correlations functions reveal the presence of a Goldstone mode associated to the quadrupolar ordering observed in Montecarlo simulations.
In the classical spin ice regime, conservation laws dictate the life of the monopoles excitations while the spin ice liquid although disordered admits coherent excitations that can be compared to spin waves. The relaxational dynamics of dopped spin ices (monopoles are introduced by reverting spins at random) also revealed that the excitations of neighboring phase although not seen in the thermodynamic quantities can still be present in the dynamical correlations functions and structure factor. These results support the general idea that a system close to a boundary between two high entropic regimes (or a spin liquid and an ordered phase) can have a thermodynamic that does not have any signature of the neighboring phase but still be influenced dynamically by it.
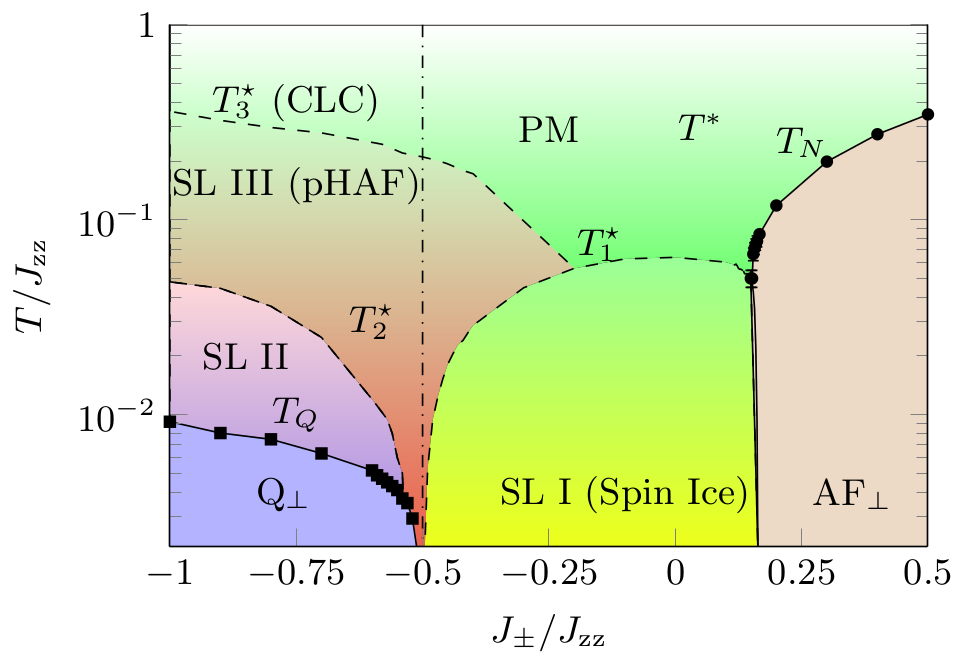
Figure 3.8: Finite–temperature phase diagram of the XXZ model on a pyrochlore lattice. The model posses three distinct spin liquid phases (SL), as well as ground states with easy–plane antiferromagnetic (AF) and quadrupolar (Q) order. Associated crossover temperatures (phase transitions) are indicated with dashed (solid) lines. For Jx00B1/Jzz = −1/2 (dash–dotted line), the model is thermo- dynamically equivalent to the Heisenberg antiferromagnet on a pyrochlore lattice. Results are taken from classical Monte Carlo simulation of a cubic cluster of N = 8192 spins.
This work was published as "Competing spin liquids and hidden spin-nematic order in spin ice with frustrated transverse exchange" Mathieu Taillefumier, Owen Benton, Han Yan, Ludovic Jaubert, and Nic Shannon Phys. Rev. X 7, 041057 (2017)
3.9 Theory of multiple-phase competition in pyrochlore magnets with anisotropic exchange with application to Yb2Ti2O7, Er2Ti2O7 and Er2Sn2O7
The pyrochlore lattice is a host to an amazing variety of exotic phases of strong correlated system. In this article we establish a general, symmetry-based theory of pyrochlore magnets with anisotropic exchange interactions. We show how the competition of different order at phase boundary could lead to exotic states of matter including spin liquids and order-by-disorder. The finite temperauter phase diagram is determined by Monte Carlo simulation, and a variety of materials s Er2Ti2O7, Yb2Ti2O7, and Er2Sn2O7 can be explained.
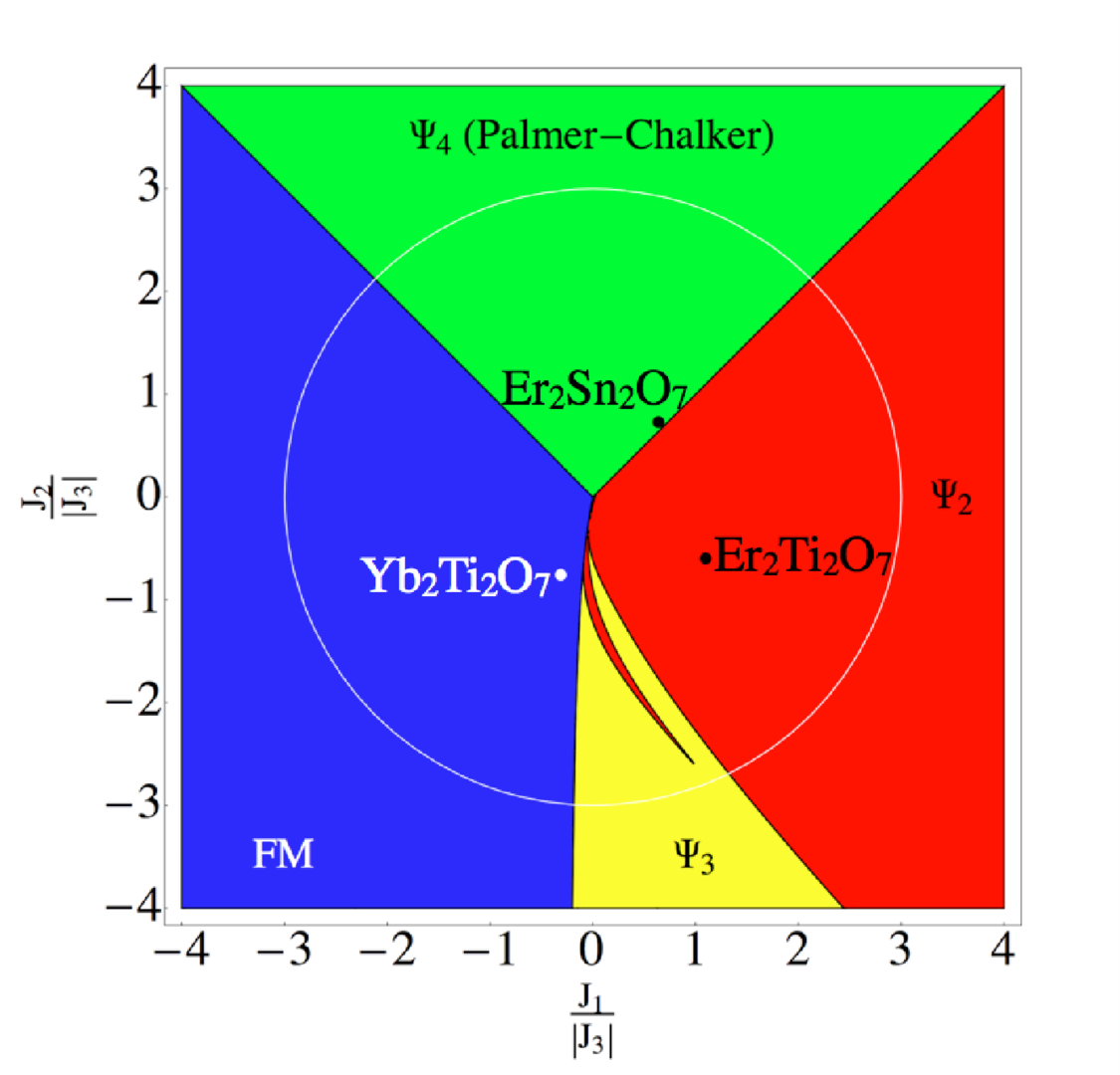
Figure 3.9: Classical ground-state phase diagram for pyrochlore magnet with anisotropic exchange interactions. There are four distinct ordered phases. Points correspond to published estimates of parameters for Yb2Ti2O7, Er2Ti2O7 and Er2Sn2O7. The white circle corresponds to the path through parameter space.
This work was published as "Theory of multiple-phase competition in pyrochlore magnets with anisotropic exchange with application to Yb2Ti2O7, Er2Ti2O7 and Er2Sn2O7", Han Yan, Owen Benton, Ludovic Jaubert and Nic Shannon Phys. Rev. B 95, 094422 (2017).
4. Publications
4.1 Journals
- D.T. Liu, F.J. Burnell, L.D.C. Jaubert and J.T. Chalker, "Classical spin liquids in stacked triangular lattice Ising antiferromagnets", Phys. Rev. B 94, 224413 (2016)
- Owen Benton, "The quantum origins of moment fragmentation in Nd2Zr2O7", Phys. Rev. B 94, 104430 (2016), Featured on the OIST website, Phys.org, Nanowerk, Technobahn, Science Daily, Alpha Galileo, Health Medicinet , Nanotech Now , Science Newsline , International News Line and EurekAlert! from the AAAS.
- M. Udagawa, L. D. C. Jaubert, C. Castelnovo and R. Moessner, "Out-of-equilibrium dynamics and extended textures of topological defects in spin ice", Phys. Rev. B 94, 104416 (2016), Selected for inclusion in Kaleidoscope.
- Rico Pohle, Owen Benton and L. D. C. Jaubert, "Reentrance of disorder in the anisotropic shuriken Ising model", Phys. Rev. B 94, 014429 (2016)
- Owen Benton, L. D. C. Jaubert, Han Yan and Nic Shannon, "A spin-liquid with pinch-line singularities on the pyrochlore lattice", Nature Communications 7, 11572 (2016), Featured on the OIST website, Phys.org, Nanowerk, Technobahn, Science Daily, Science Newsline, Alpha Galileo and EurekAlert! from the AAAS.
- Andrew Smerald and Nic Shannon, "Theory of the NMR 1/T_1 relaxation rate in a quantum spin nematic in applied magnetic field", Phys. Rev. B 93, 184419 (2016)
- Han Yan, Owen Benton, Ludovic Jaubert, and Nic Shannon, "Theory of multiple-phase competition in pyrochlore magnets with anisotropic exchange with application to Yb2Ti2O7, Er2Ti2O7, and Er2Sn2O7" PhysRevB.95.094422 (2017)
4.2 Books and other one-time publications
Nothing to report.
4.3 Oral and Poster Presentations
Invited Oral Presentations:
- Karim Essafi, "A Kagome Map of Spin Liquids", Stockholm University, Sweden (2017.02.20)
- Nic Shannon “Quantum Water Ice”, Keynote, International Symposium on Eco-materials Processing and Design, Naha, Okinawa (2017.02.18)
- Karim Essafi, "Lifshitz Critical Behaviour", Royal Institute of Technology, Stockholm, Sweden (2017.02.17)
- Karim Essafi, "A Kagome Map of Spin Liquids", Utrecht University, Netherland (2017.02.14)
- Judit Romhányi "Chernful excitations in 2D quantum magnets", Workshop on Theory of Correlated Topological Materials, ISSP, University of Tokyo (2017.02.14)
- Karim Essafi, "A Kagome Map of Spin Liquids", Technical University of Munich, Germany (2017.02.10)
- Karim Essafi, "A Kagome Map of Spin Liquids", University Pierre and Marie Curie, Paris, France (2017.02.06)
- Rico Pohle, "Symmetry and optical selection rules in graphene quantum dots", University of Tokyo (2017.02.01)
- Ludovic Jaubert, "When spin liquids order ... but just a bit", Institute for Basic Science (PCS), Daejeon, South Korea (2017.01.05)
- Ludovic Jaubert, “When spin liquids order ... but just a bit”, Statphys Kolkata IX, Kolkata, India (2016.12.16)
- Nic Shannon, “Quantum spin nematics”, University of New South Wales, Sydney, Australia (2016.12.13)
- Nic Shannon, “Quantum Spin Ice”, University of Queensland, Brisbane, Australia (2016.12.09)
- Judit Romhányi, "Spin-Orbit Dimers and Non-Collinear Phases in d1 Cubic Double Perovskites", AHMF & Cadet Program Joint Seminar, Osaka University (2016.12.08)
- Nic Shannon, “Quantum spin nematics”, Joint Asia Pacific Physics Conference and Australian Institute of Physics Congress, Brisbane, Australia (2016.12.07)
- Ludovic Jaubert, “When spin liquids order ... but just a bit.”, International Centre for Theoretical Science, Bangalore, India (2016.12.07)
- Nic Shannon, “Quantum Spin Nematics”, JPS Meeting, Kanazawa University (2016.09.15)
- Karim Essafi, “A Kagome Map of Spin Liquids”, National Center for Theoretical Sciences, Hsinchu, Taiwan (2016.09.12)
- Nic Shannon, “Quantum Spin Nematics”, HFM2016, Taipei, Taiwan (2016.09.08)
- Nic Shannon, “Quantum Spin Nematics”, MPI-FKF, Stuttgart, Germany (2016.08.19)
- Nic Shannon, “Quantum Spin Nematics”, University of Bristol, UK (2016.08.15)
- Ludovic Jaubert, “Magnetic Crystallography in Spin Ice”, National Cheng Kung University, Taiwan (2016.07.29)
- Nic Shannon, “Spin-Orbital Physics: Important Open Problems and Outlook”, Summary talk as part of panel discussion in the workshop : “New Quantum Phases with Entanglement and Frustration”, Cracow, Poland (2016.06.22)
- Judit Romhanyi “Magneto-electric control of toroidic moments in multiferroic LiCoPO4”, New Quantum Phases with Frustration and Entanglement, Jagiellonian University, Cracow, Poland (2016.06.21)
- Nic Shannon, “Quantum Water Ice”, Workshop on New Quantum Phases with Frustration and Entanglement, Jagiellonian University, Cracow, Poland (2016.06.21)
- Nic Shannon, “Quantum Spin Nematics”, Jagiellonian University, Krakow (2016.06.17)
- Nic Shannon, “Quantum Spin Nematics”, ISSP, University of Tokyo (2016.05.11)
Contributed Oral Presentations:
- Rico Pohle, Han Yan, Nic Shannon,"Origin of quantum spin liquid phase in Ca10Cr7O28", JPS Meeting, Osaka University (2017.03.18)
- Yurika Kubo and Susumu Kurihara, “Formalism of Spin and Energy Conductivity in Magnetic Insulators” APS March Meeting, New Orleans, USA (2017.03.17)
- Han Yan, Rico Pohle, Nic Shannon,"Origin of quantum spin liquid phase in Ca10Cr7O28", APS March Meeting, New Orleans, USA (2017.03.16)
- Nic Shannon, Mathieu Taillefumier, John Owen Benton, Ludovic Jaubert, "Quadrupolar Order in Quantum Spin Ice", APS March Meeting, New Orleans, USA (2017.03.15)
- Judit Romhányi. "Chernful excitations in 2D quantum magnets", APS March Meeting, New Orleans, USA (2017.03.13)
- Judit Romhanyi, George Jackeli, “Spin-Orbit Dimers in Double Perovskites”, JPS Meeting, Kanazawa University (2016.09.16)
- Rico Pohle,Ludovic Jaubert, “様々なフラストレートスピン系におけるキュリー法則のクロスオーバー/ Curie–law and Crossover in a Variety of Classical Spin Liquids” (talk in Japanese), JPS Meeting, Kanazawa University (2016.09.16)
- Ludovic Jaubert, Karim Essafi, John Owen Benton, "Is kagome more frustrated than pyrochlore ?", JPS Meeting, Kanazawa University (2016.09.16)
- Ludovic Jaubert, Karim Essafi, Masafumi Udagawa "A phase diagram of breathing pyrochlores" , JPS Meeting, Kanazawa University (2016.09.14)
- Ludovic Jaubert, Taoran Lin, Tuba S Opel, Peter Holdsworth, Michel Gingras, “Spin Ice Thin Film: Surface Freezing and Emergent Square Ice”, JPS Meeting, Kanazawa University (2016.09.14)
- Ludovic Jaubert, Karim Essafi, John Owen Benton, Han Yan, Nic Shannon, “Cooking with spin-orbit coupling : a recipe for spin liquids” HFM2016, Taipei, Taiwan (2016.09.10)
- Ludovic Jaubert, “A kagome map of spin liquids”, StatPhys26, Lyon, France (2016.07.22)
- Nic Shannon, Owen Benton, Han Yan, Ludovic Jaubert, "A new spin liquid on the pyrochlore lattice", StatPhys26, Lyon, France (2016.07.19)
Conference Poster Presentations:
- Owen Benton, Ludovic Jaubert, Han Yan, Nic Shannon "Spin Liquid on Pyrochlore Lattice with Pinch-Line Singularities", International School on Topological Science and Topological Matter, YITP, Kyoto University (2017.02.17)
- Yurika Kubo and Susumu Kurihara “Formalism of spin and thermal conductivity in localized magnets” in International School on Spintronics & Spin-Orbitronics, Fukuoka, Japan (2016.12.16)
- John Owen Benton, “The quantum origins of magnetic fragmentation in Nd2Zr2O7”, HFM2016, NTU Convention Center, Taipei, Taiwan (2016.09.08)
- Mathieu Taillefumier, John Owen Benton, Nic Shannon, “Thermodynamics and semi-classical dynamics of a quantum spin ice : competing antiferromagnetism and the fate of magnetic monopoles”, HFM2016, Taipei, Taiwan (2016.09.08)
- Judit Romhányi and George Jackeli, "Disordered spin-orbital dimer state in double-perovskite compounds", HFM2016, Taipei, Taiwan (2016.09.08)
- Rico Pohle, Mathieu Taillefumier, John Owen Benton, Ludovic Jaubert, Nic Shannon, “The shuriken lattice: reentrance and order- by disorder”, HFM2016, Taipei, Taiwan (2016.09.08)
- Han Yan, John Owen Benton, Ludovic Jaubert, Nic Shannon, “Spin Liquid on Pyrochlore Lattice with Pinch-Line Singularities” HFM2016, Taipei, Taiwan (2016.09.08)
- Karim Essafi, Ludovic Jaubert and Masafumi Udagawa, "Flat Bands and Dirac Cones in Breathing Lattices", HFM2016, Taipei, Taiwan (2016.09.08)
- Yurika Kubo and Susumu Kurihara, “Sum Rule of Thermal and Spin Conductivity in Antiferromagnets” in ASCES2016, Minneapolis, U. S. A (2016.06.13)
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report.
6. Meetings and Events
6.1 Research Visits and Seminars
|
|
Geet Rakala - PhD Student, Tata Institute of Fundamental Research
|
 |
Jun Won Rhim - Postdoc, MPI-PKS Dresden
|
 |
Hiroshi Kageyama - Professor, Kyoto University
|
 |
Olga Sikora - Adjunkt, Jagiellonian University
|
 |
Keisuke Totsuka - Associate Professor, YITP Kyoto University
|
 |
Claudio Castelnovo - Associate Professor, University of Cambridge
|
 |
Hiroaki Ueda - Lecturer, Toyama Prefectural University
|
 |
Yuan Wan - Postdoc, Perimeter Institute for Theoretical Physics
|
 |
Yutaka Akagi - Assistant Professor, University of Tokyo
|
 |
Andrew Smerald - Postdoc, EPFL Lausanne
|
 |
Tomonari Mizoguchi - Ph.D. student, University of Tokyo
|
 |
Masafumi Udagawa - Associate Professor, Gakushuin University
|
 |
Tokuro Shimokawa - Postdoc, Osaka University
|
7. Other



