2D FFT With Simultaneous Edge Artifact Removal (No. 0084)
|
|
|
<< Back to all technologies |
Summary
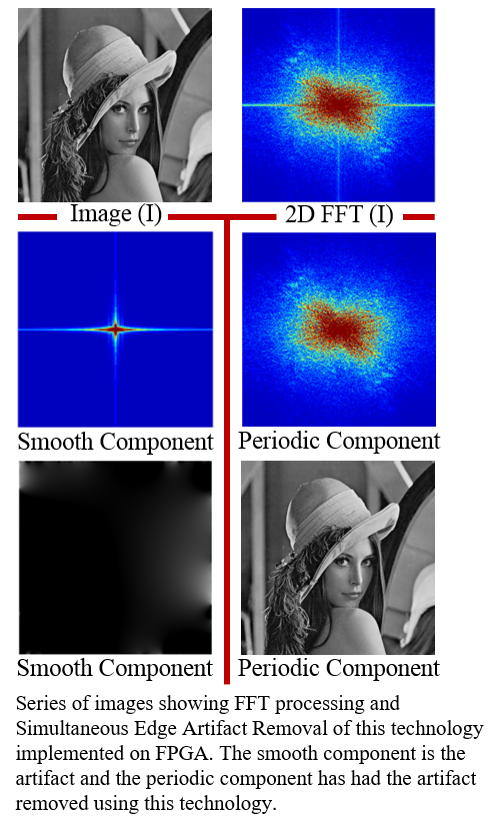
The growth of the diagnostic imaging market is primarily driven by the increasing demand for early disease diagnosis and widening scope of clinical applications. 2D Fast Fourier Transforms (FFTs) have become a computational constraint because FFTs inherently assume that image edges are periodic leading to high amplitude “cross-shaped” artifacts in the frequency domain. These artifacts can be propagated to later stages of processing, adversely affecting decision critical applications, such as, medical diagnostics. Here, we present a promising imaging algorithm developed by a group of researchers led by Prof. Ulf Skoglund. The developed algorithm simultaneously removes edge artifacts by decomposing the image into periodic and smooth components in real-time unlike existing technologies such as windowing and mirroring which require more computational burden.
Applications
- High speed industrial tracking
- Medical diagnostics (MRI, CT, etc.)
- Electron microscopy
- Astronomical imaging
- Image processing (convolution)
Advantages
- Real-time processing
- Minimization of artifacts
- 100 fps for 2048 x 2048 pixel image
Technology
This invention represents a new approach based on periodic plus smooth decomposition, specifically optimized to reduce DRAM access and to decrease 1D FFT invocations. A “tile-hopping” memory mapping scheme is used to significantly improve the bandwidth of the external memory for column-wise reads and to reduce energy consumption. These optimizations allow an efficient 2D FFT implementation based on FPGAs and lead to a high-performance solution for removing edge artifacts while the transform is being calculated, thereby obviating the need for time-consuming and possibly erroneous postprocessing steps.
Media Coverage and Presentations
![]() JST Technology Showcase Presentation
JST Technology Showcase Presentation
![]() JST Technology Showcase Presentation Slides
JST Technology Showcase Presentation Slides
CONTACT FOR MORE INFORMATION
![]() Graham Garner
Graham Garner
Technology Licensing Section
![]() tls@oist.jp
tls@oist.jp
![]() +81(0)98-966-8937
+81(0)98-966-8937