FY2021 Annual Report
Qubits and Spacetime Unit
Assistant Professor Philipp Höhn
Abstract
In the second year of the unit, the Japanese borders finally opened for postdocs and the first four arrived in-person at OIST between June and October 2021. This boosted unit activities, including joint research projects as well as student supervision.
The research of the unit in FY21 focused on quantum reference frames, dynamical frames in generally covariant theories, edge modes and finite regions in gauge theories and gravity, and quantum cosmology.
1. Staff
- Dr. Joshua Kirklin, Postdoctoral Scholar
- Dr. Isha Kotecha, Postdoctoral Scholar
- Dr. Fabio Maria Mele, Postdoctoral Scholar
- Dr. Stefan Eccles, Postdoctoral Scholar
- Mr. Snigdh Sabharwal, Rotation student (May-Aug, 2021)
- Joshua Carlo Casapao Aparicio, Rotation student (Sep-Dec, 2021)
- Tatiana Iakovleva, Rotation student (Sep-Dec, 2021)
- Julian De Vuyst, Rotation student (Jan-April 2022)
- Andreani Petrou, Rotation student (Jan-April 2022)
- Victor Castillo-Martinez, Research Intern (November 2021 - )
- Giovanni Natale, Research Intern (November 2021 - )
- Midori Tanahara, Administrative Assistant
2. Collaborations
2.1 Internal quantum reference frames for finite abelian groups
- Description: Preprint appeared in July 2021 (submitted for publication).
- Type of collaboration: Joint research
- Researchers:
- Prof. Philipp Höhn, OIST
- Dr. Markus Müller, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Marius Krumm, Institute for Quantum Optics and Quantum Information, Vienna, Austria
2.2 Edge modes as reference frames and boundary actions from post-selection
- Description: Preprint appeared in September 2021 and is now published in JHEP.
- Type of collaboration: Joint research
- Researchers:
- Dr. Sylvain Carrozza, University of Nijmegen, The Netherlands
- Prof. Philipp Höhn, OIST
2.3 Perspective-neutral approach to quantum frame covariance for general symmetry groups
- Description: Preprint appeared in October 2021 (submitted for publication).
- Type of collaboration: Joint research
- Researchers:
- Anne-Catherine de la Hamette, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Dr. Thomas Galley, Perimeter Institute for Theoretical Physics, Waterloo, Canada
- Prof. Philipp Höhn, OIST
- Dr. Leon Loveridge, University of South-Eastern Norway
- Dr. Markus Müller, Institute for Quantum Optics and Quantum Information, Vienna, Austria
2.4 The physical relevance of the fiducial cell in loop quantum cosmology
- Description: Preprint appeared in September 2021 (submitted for publication)
- Type of collaboration: Joint research
- Researchers:
- Dr. Fabio Mele, OIST
- Dr. Johannes Münch, CPT Marseille
2.5 Edge modes as dynamical frames: charges from post-selection in generally covariant theories
- Description: Preprint appeared in May 2022.
- Type of collaboration: Joint research
- Researchers:
- Dr. Sylvain Carrozza, University of Nijmegen, The Netherlands
- Dr. Stefan Eccles, OIST
- Prof. Philipp Höhn, OIST
2.6 Diffeomorphism-invariant observables and dynamical frames in gravity: reconciling bulk locality with general covariance
- Description: Preprint appeared in June 2022.
- Type of collaboration: Joint research
- Researchers:
- Dr. Christophe Goeller, LMU München, Germany
- Prof. Philipp Höhn, OIST
- Dr. Josh Kirklin, OIST
2.7 Quantm relativity of thermality
- Description: ongoing.
- Type of collaboration: Joint research
- Researchers:
- Dr. Isha Kotecha, OIST
- Dr. Fabio Mele, OIST
- Prof. Philipp Höhn, OIST
2.8 Geometry from correlators in gauge theories
- Description: ongoing.
- Type of collaboration: Joint research
- Researchers:
- Victor Castillo-Martinez, OIST
- Prof. Philipp Höhn, OIST
2.9 Informational charges in systems of qubits
- Description: ongoing.
- Type of collaboration: Joint research
- Researchers:
- Prof. Philipp Höhn, OIST
- Giovanni Natale, OIST
- Dr. Chris Wever, Bosch Quantum Computing
2.10 Relational Dynamics with periodic clocks
- Description: ongoing.
- Type of collaboration: Joint research
- Researchers:
- Dr. Max Lock, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Dr. Leonardo Chataignier, University of Bologna, Italy
2.11 Quantum covariant field theory
- Description: ongoing.
- Type of collaboration: Joint research
- Researchers:
- Prof. Philipp Höhn, OIST
- Andrea Russo, University College London, UK
- Prof. Alex Smith, Dartmouth College & St. Anselm College, USA
3. Activities and Findings
We only describe activities and findings of projects completed (and published on arXiv) during FY21.
3.1 Internal quantum reference frames for finite abelian groups
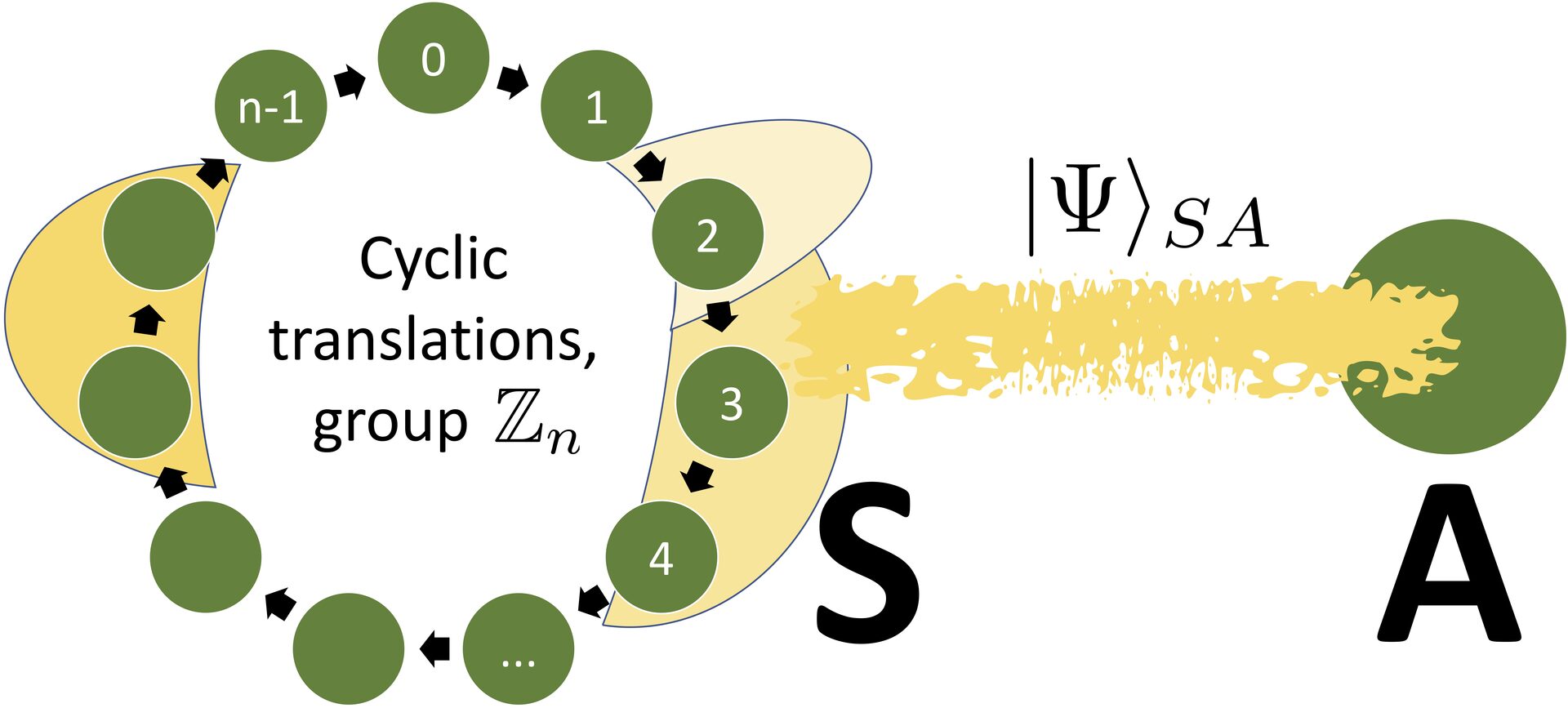
Employing internal quantum systems as reference frames is a crucial concept in quantum gravity, gauge theories and quantum foundations whenever external relata are unavailable. In joint work with Marius Krumm and Markus Müller from IQOQI Vienna, we gave a comprehensive and self-contained treatment of such quantum reference frames (QRFs) for the case when the underlying configuration space is a finite Abelian group, significantly extending our previous work. The simplicity of this setup admits a fully rigorous quantum information-theoretic analysis, while maintaining sufficient structure for exploring many of the conceptual and structural questions also pertinent to more complicated setups. We exploited this to derive several important structures of constraint quantization with quantum information-theoretic methods and to reveal the relation between different approaches to QRF covariance. In particular, we characterized the "physical Hilbert space" - the arena of the "perspective-neutral" approach - as the maximal subspace that admits frame-independent descriptions of purifications of states. We then demonstrated the kinematical equivalence and, surprising, dynamical inequivalence of the "perspective-neutral" and the "alignability" approach to QRFs. While the former admits unitaries generating transitions between arbitrary subsystem relations, the latter, remarkably, admits no such dynamics when requiring symmetry-preservation. We illustrated these findings by example of interacting discrete particles, including how dynamics can be described "relative to one of the subystems".
Figure 1: Some finite abelian group (here \(\mathbb{Z}_n\)) assumes as double role: (1) as a discrete configuration space for a system \(S\), (2) as a translation group on that configuration space. We considered internal quantum reference frames associated with such finite groups and derived a number or properties. For example, we showed that gauge-invariant states (living in the trivial representation of the group) comprise the maximal subspace of states of \(S\) that admit frame-independent purifications.
Publication: Philipp A. Höhn, Marius Krumm, and Markus P. Müller, "Internal quantum reference frames for finite Abelian groups", arXiv:2107.07545
3.2 Edge modes as reference frames and boundary actions from post-selection
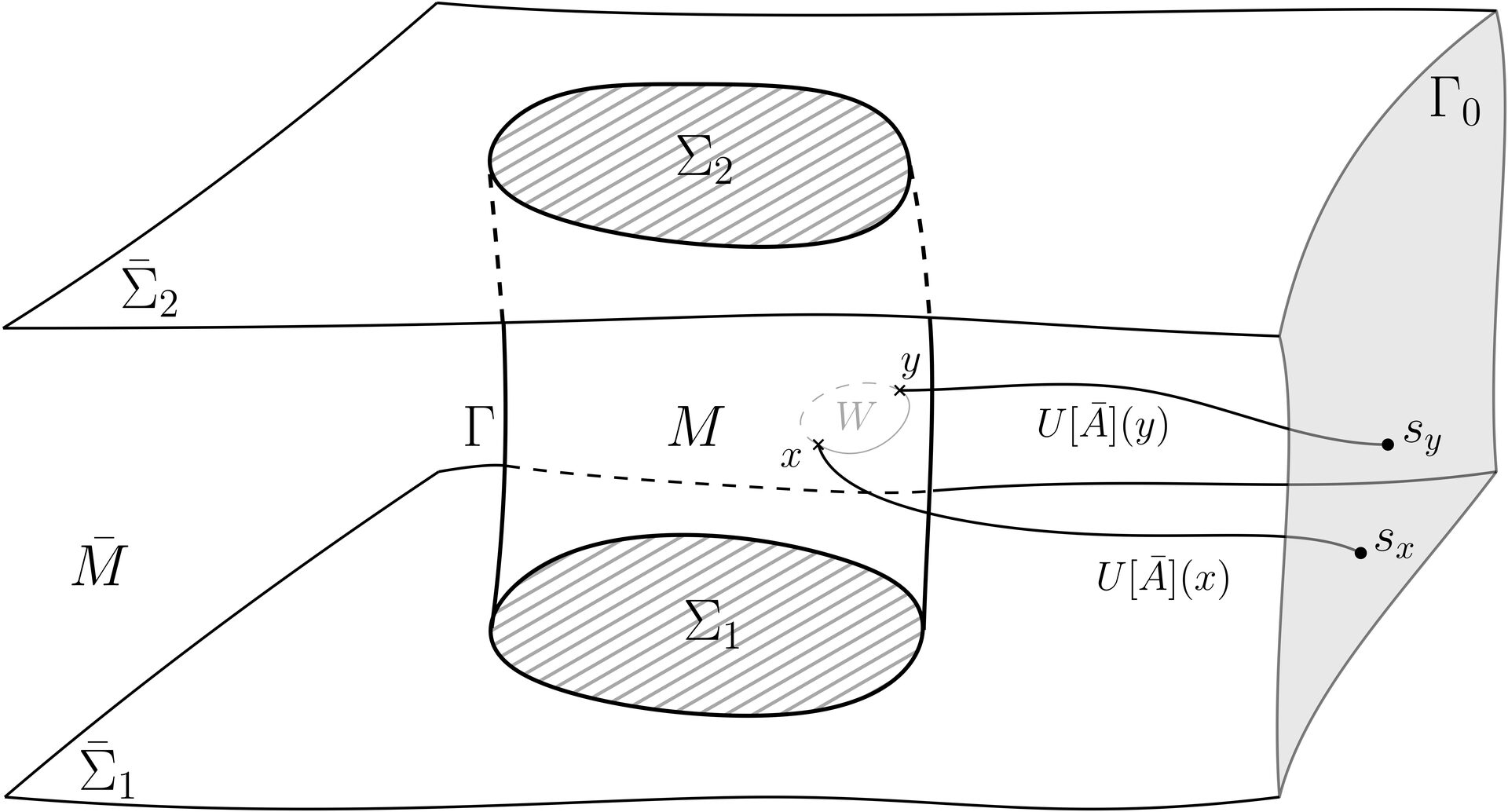
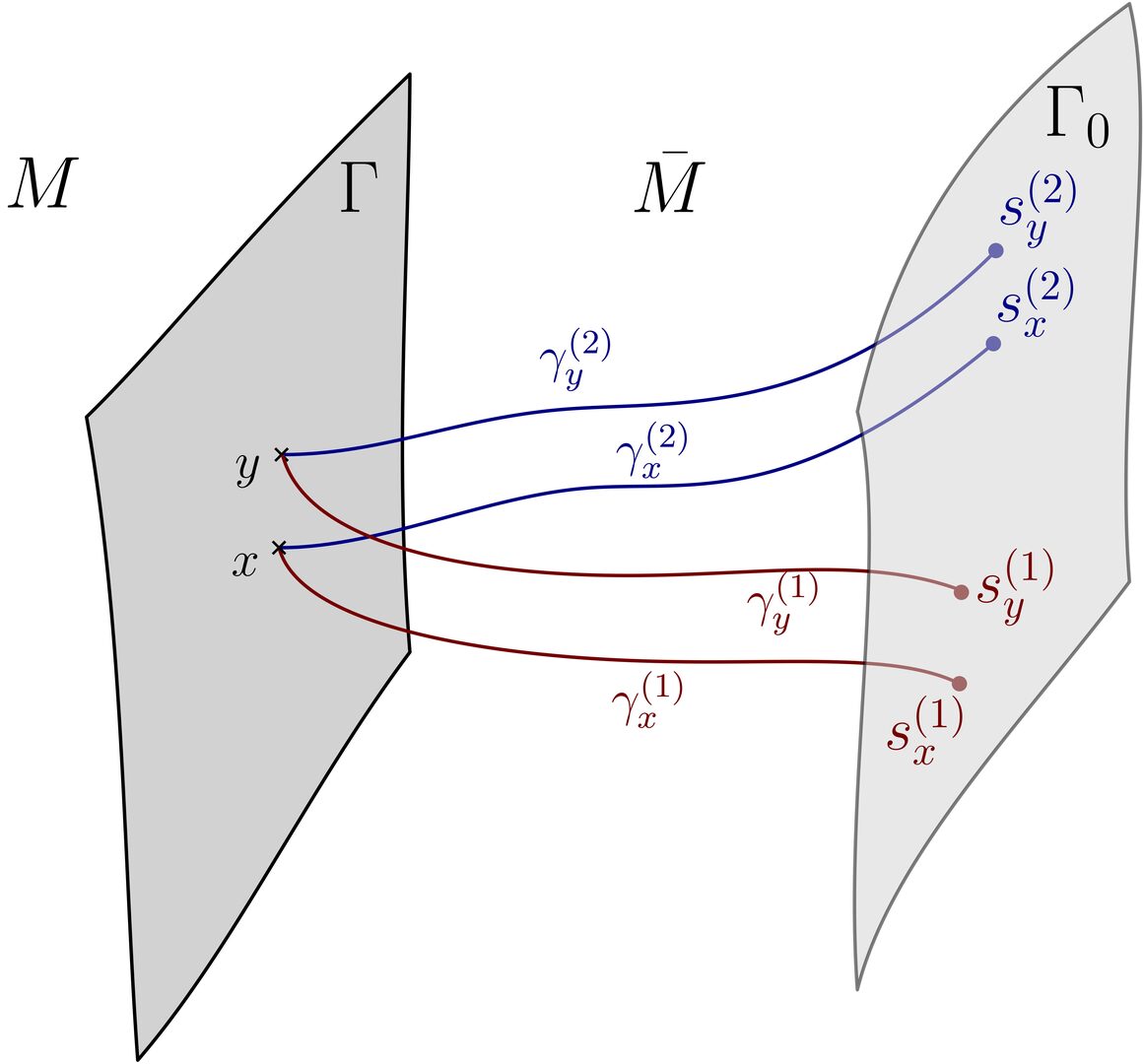
Together with Dr. Sylvain Carrozza from IMAPP Nijmegen, we introduced a general framework realizing edge modes in (classical) gauge field theory as dynamical reference frames, an often suggested interpretation that we made entirely explicit. We focused on a bounded region \(M\) with a co-dimension one time-like boundary \(\Gamma\), which we embedded in a global spacetime. Taking as input a variational principle at the global level, we developed a systematic formalism inducing consistent variational principles (and in particular, boundary actions) for the subregion \(M\). This relied on a post-selection procedure on \(\Gamma\), which isolates the subsector of the global theory compatible with a general choice of gauge-invariant boundary conditions for the dynamics in \(M\). Crucially, the latter relate the configuration fields on \(\Gamma\) to a dynamical frame field carrying information about the spacetime complement of \(M\); as such, they may be equivalently interpreted as frame-dressed or relational observables. Generically, the external frame field keeps an imprint on the ensuing dynamics for subregion \(M\), where it materializes itself as a local field on the time-like boundary \(\Gamma\); in other words, an edge mode. We identified boundary symmetries as frame reorientations and showed that they divide into three types, depending on the boundary conditions, that affect the physical status of the edge modes. Our construction relied on the covariant phase space formalism, and is in principle applicable to any gauge (field) theory. We illustrated it on three standard examples: Maxwell, Abelian Chern-Simons and non-Abelian Yang-Mills theories. In complement, we also analyzed a mechanical toy-model to connect our work with recent efforts on (quantum) reference frames.
|
|
|
| Figure 2: Configuration of finite spacetime subregion \(M\) inside the global piece \(M\cup \bar M\). \(M \) is delimited by the timelike boundary \(\Gamma\) and partial Cauchy slices \(\Sigma_1\) and \(\Sigma_2\). \(\Gamma_0\) is some distant (possibly asymptotic) boundary. Edge modes on the finite boundary \(\Gamma\) can be realized, for example, via Wilson lines shot in from \(\Gamma_0\). While from the point of view of the global theory, these edge modes are composite, non-local degrees of freedom, they appear as "new" from the point of view of the subregion theory. They are group-valued degrees of freedom that constitute internal reference frames associated with the structure group of the gauge theory. The edge-frame-dressed observables on \(\Gamma\) thereby describe in a gauge-invariant manner how the subregion \(M\) relates to its complement \(\bar M\). Edge modes can be viewed as "internalized" external reference frames for the subregion of interest. |
Figure 3: Different systems of paths shot in from \(\Gamma_0\) yield different systems of Wilson lines and thus different edge mode frames on \(\Gamma\). We developed a method for changing between the gauge invariant descriptions relative to different choices of edge frame.
|
Publication: Sylvain Carrozza and Philipp A. Höhn, "Edge modes a reference frames and boundary actions from post-selection", JHEP 02 72 (2022), arXiv:2109.06184
3.3 Perspective-neutral approach to quantum frame covariance for general symmetry groups
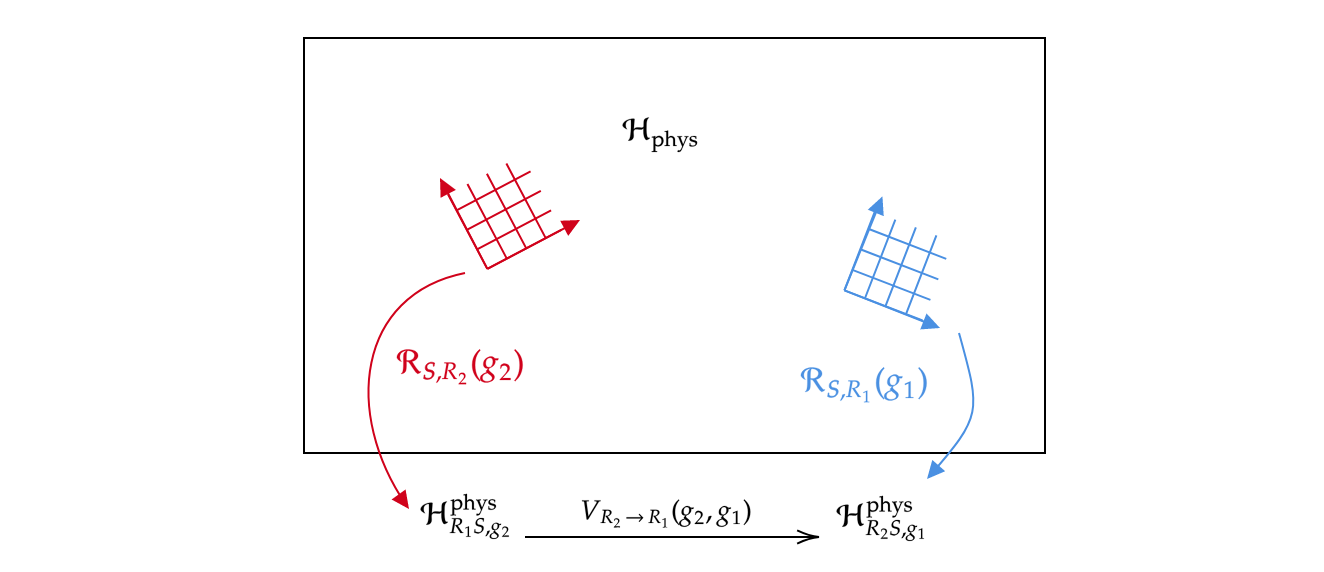
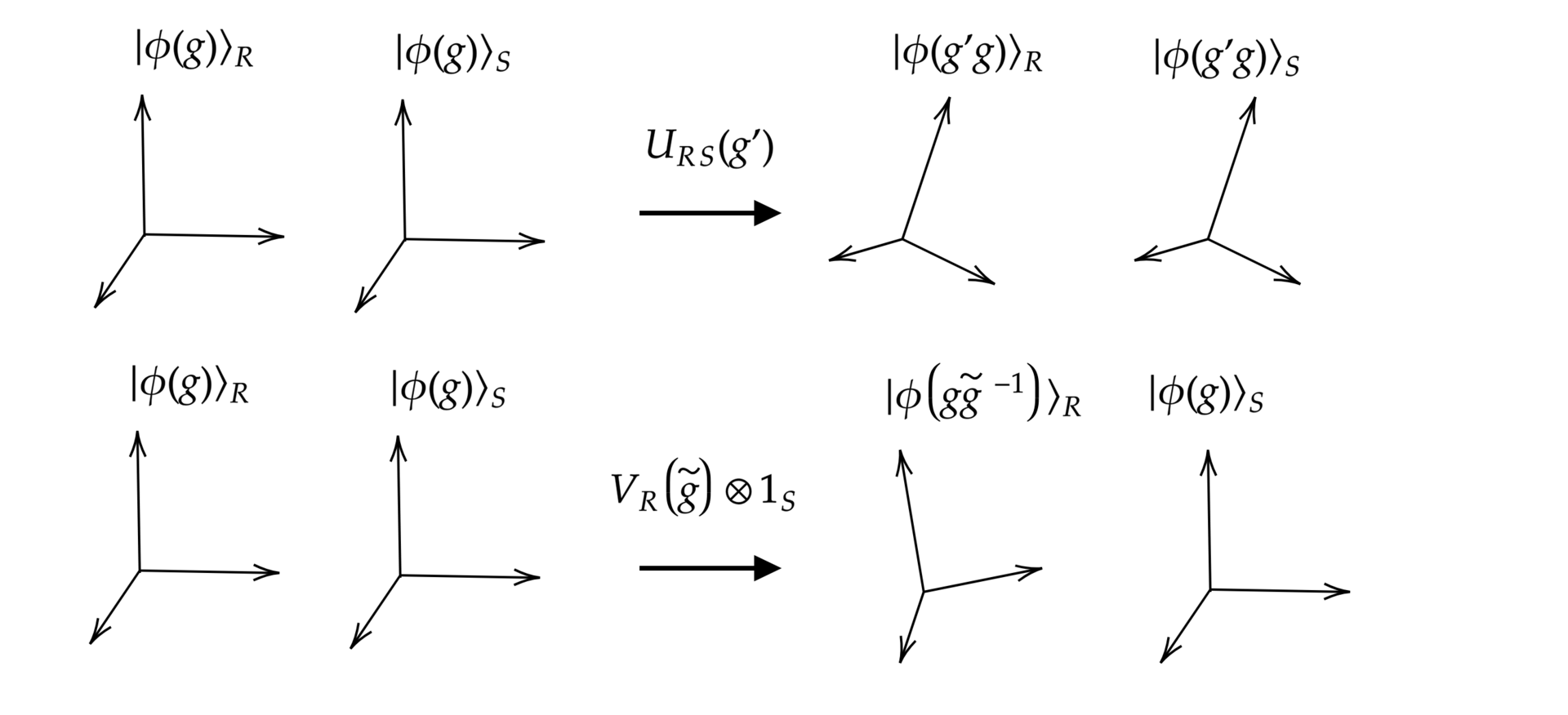
In the absence of external relata, internal quantum reference frames (QRFs) appear widely in the literature on quantum gravity, gauge theories and quantum foundations. In this project, we extended the perspective-neutral approach to QRF covariance to general unimodular Lie groups together with four external collaborators. This is a framework that links internal QRF perspectives via a manifestly gauge-invariant Hilbert space in the form of "quantum coordinate transformations", and we clarified how it is a quantum extension of special covariance. We modelled the QRF orientations as coherent states which give rise to a covariant POVM, furnishing a consistent probability interpretation and encompassing non-ideal QRFs whose orientations are not perfectly distinguishable. We generalized the construction of relational observables, establish a variety of their algebraic properties and equip them with a transparent conditional probability interpretation. We imported the distinction between gauge transformations and physical symmetries from gauge theories and identified the latter as QRF reorientations. The "quantum coordinate maps" into an internal QRF perspective were constructed via a conditioning on the QRF's orientation, generalizing the Page-Wootters formalism and a symmetry reduction procedure. We found two types of QRF transformations: gauge induced "quantum coordinate transformations" as passive unitary changes of description and symmetry induced active changes of relational observables from one QRF to another. We revealed new effects: (i) QRFs with non-trivial orientation isotropy groups can only resolve isotropy-group-invariant properties of other subsystems; (ii) in the absence of symmetries, the internal perspective Hilbert space "rotates" through the kinematical subsystem Hilbert space as the QRF changes orientation. Finally, we invoked the symmetries to generalize the quantum relativity of subsystems before comparing with other approaches.
 |
|
| Figure 4: distinction between gauge transformations (up) and symmetries as frame reorientations (down) for the rotation group. | Figure 5: "Quantum coordinate transformations" mapping between two internal quantum frame perspectives. |
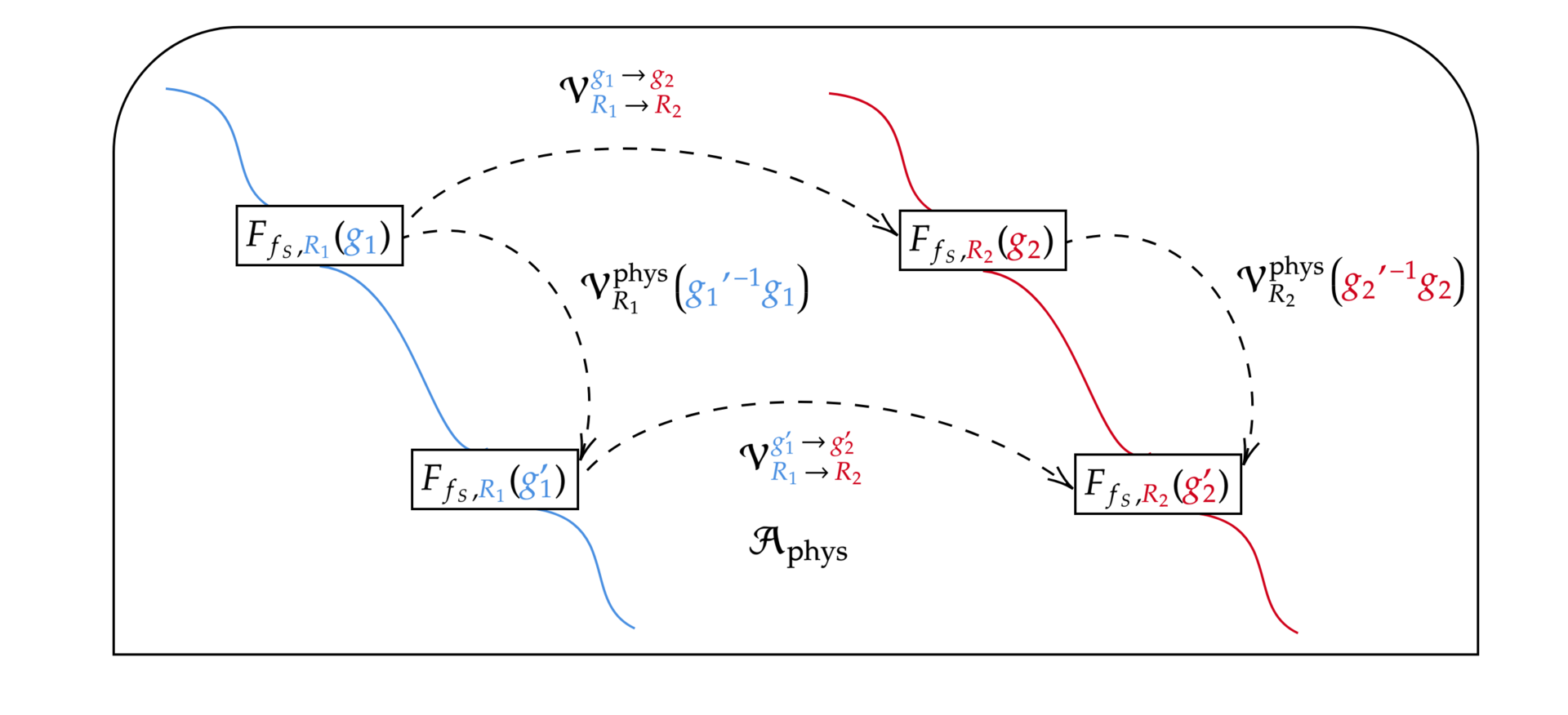
Figure 6: Symmetry-induced quantum frame transformations, changing from the relational observables relative to one frame to those relative to another. Relational observables define orbits in the algebra of gauge-invariant observables and the frame transformations map between these orbits.
Publication: Anne-Catherine de la Hamette, Thomas D. Galley, Philipp A. Höhn, Leon Loveridge and Markus P. Müller, "Perspective-neutral approach to quantum frame covariance for general symmetry groups", arXiv:2110.13824
3.4 The physical relevance of the fiducial cell in loop quantum cosmology
A common way to avoid divergent integrals in homogeneous spatially non-compact gravitational systems, as e.g. cosmology, is to introduce a fiducial cell by cutting-off the spatial slice at a finite region \(V_0\). This is usually considered as an auxiliary integral regulator to be removed after performing computations by sending it to infinity. In a project with Johannes Münch, our postdoc Fabio Mele analysed the dependence of the classical and quantum theory of homogeneous, isotropic and spatially flat cosmology on this fiducial cell. They showed that each fixed \(V_0\) regularisation leads to a different canonically independent theory. At the classical level, the dynamics of observables is not affected by the regularisation choice on-shell. For the quantum theory, however, this leads to a family of regulator dependent quantum representations labelled by \(V_0\) and the limit \(V_0\to\infty\) becomes then more subtle. First, they constructed a novel isomorphism between different \(V_0\)-regularisations, which allowed them to identify states in the different \(V_0\)-labelled Hilbert spaces to ensure equivalent dynamics for any value of the regulator. The \(V_0\to\infty\) limit would then correspond to choosing a state for which the volume assigned to the fiducial cell becomes infinite. As second main result of their analysis, by looking at observables respectively smeared over the fiducial cell \(V_0\) and subregions \(V\), they found that quantum fluctuations of the latter explicitly depend on the size of the fiducial cell. Physically relevant fluctuations for a finite region, as e.g. in the early time regime, would then be unreasonably suppressed in the limit where the volume of the fiducial cell becomes infinite. Their results suggest that the fiducial cell is not playing the role of a mere regularisation but is physically relevant at the quantum level and complement previous statements in the literature based on different arguments.
Publication: Fabio Mele and Johannes Münch, "The Physical Relevance of the Fiducial Cell in Loop Quantum Cosmology", arXiv:2109.10663
4. Publications
4.1 Journals
The list includes preprints finished in FY20 and FY19, but published in FY21.
- Anne-Catherine de la Hamette, Thomas D. Galley, Philipp A. Höhn, Leon Loveridge and Markus P. Müller, "Perspective-neutral approach to quantum frame covariance for general symmetry groups", arXiv:2110.13824
- Fabio Mele and Johannes Münch, "The Physical Relevance of the Fiducial Cell in Loop Quantum Cosmology", arXiv:2109.10663
- Sylvain Carrozza and Philipp A. Höhn, "Edge modes a reference frames and boundary actions from post-selection", JHEP 02 72 (2022), arXiv:2109.06184
- Philipp A. Höhn, Marius Krumm, and Markus P. Müller, "Internal quantum reference frames for finite Abelian groups", arXiv:2107.07545
- Shadi Ali Ahmad, Thomas D. Galley, Philipp A. Höhn, Maximilan P. E. Lock and Alexander R. H. Smith, "Quantum Relativity of Subsystems", Phys.Rev.Lett. 128 (2022) 17, 170401, arXiv:2103.01232
- Fabio Mele, Johannes Münch, and Stratos Pateloudis, "Quantum corrected polymer black hole thermodynamics: Mass relations and logarithmic entropy corrections", JCAP 02 (2022) 011, arXiv:2102.04788
- Josh Kirklin, "Islands and Uhlmann phase: Explicit recovery of classical information from evaporating black holes", J. High Energ. Phys. 2022, 119 (2022), arXiv:2011.07086
- Marius Krumm, Philipp A. Höhn, and Markus P. Müller 2021, "Quantum reference frame transformations as symmetries and the paradox of the third particle", Quantum 5, 530, Preprint arXiv:2011.01951
- P. A. Höhn, A. Smith and M. Lock 2021, "Equivalence of approaches to relational quantum dynamics
in relativistic settings", Front. Phys. 9:587083, invited contribution to special issue "Qubits and Spacetime" - P. A. Höhn, A. Smith and M. Lock 2021, "The trinity of relational quantum dynamics", Phys. Rev. D 104 066011, Preprint arXiv:1912.00033
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Philipp Höhn, "Quantum frame covariance", March 17 2022, DAMTP Seminar, University of Cambridge (not recorded)
- Philipp Höhn, "Progress in relational quantum dynamics", Nov 5 2021, Theory of Relativity Seminar, @ University of Warsaw (video)
- Philipp Höhn, "Progress in relational quantum dynamics", Sep 1 2021, Time in Quantum Theory, Workshop @ ETH Zürich (recording)
- Philipp Höhn, "(Quantum) frame covariance in gauge systems and gravity", Aug 16 2021, QASTM Seminar (video)
- Philipp Höhn, "(Quantum) frame covariance: from foundations via gauge theories to gravity", June 16 2021, Quantizing Time, Workshop @ Perimeter Institute (video)
- Philipp Höhn, "(Quantum) frame covariance in gauge systems and gravity", May 18 2021, Non-local Quantum Gravity Seminar, ENS Lyon (video)
- Isha Kotecha, "Generalised Gibbs States and Application in Discrete Quantum Gravity", May 12 2021, Cosmology, Relativity and Gravitation (CRAG) seminar, University of Sheffield (online)
-
Philipp Höhn, Discussion Panel Member "Observables in quantum gravity", April 8 2021, Quantum Gravity Across Approaches Initiative (video)
-
Josh Kirklin, "Uhlmann Phase, Black Hole Information and Holography", April 8 2021. QASTM online seminar series (video)
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Online QUAST Seminars
Videos can be found here.
- Josiah Couch, Boston College - 29 Mar 2022. Pants Decomposition as Circuit Complexity in 2D (T)QFT
- Antony Speranza, University of Illinois Urbana-Champaign - 15 Mar 2022. Local gravitational charges and their algebra
- Jinzhao Wang, ETH Zurich - 7 Mar 2022. The black hole information puzzle and the quantum de Finetti theorem
- Lucas Hackl, University of Melbourne - 28 Feb 2022. Volume-law entanglement entropy of typical pure quantum states
- Stefan Eccles, OIST - 7 Feb 2022. Information spreading in chaotic quantum systems
- Phuc Nguyen, City University of New York and University of Haifa - 1 Feb, 2022. Scrambling and the black hole atmosphere
- Laurent Freidel, Perimeter Institute - 10 Dec, 2021. Local Holography: A quantum gravity paradigm to construct gravitational subsystems
- Robert Oeckl, UNAM - 7 Dec, 2021. Hands on with the positive formalism
- Slava Lysov, OIST - 15 Nov, 2021. Phase space on surface with the boundary via symplectic reduction
- Francesco Sartini, ENS Lyon - 8 Nov, 2021. Hidden symmetries in black holes
- Yasha Neiman, OIST - 27 Oct. A microscopic derivation of the quantum measurement postulates
- Fabio Anza, UC Davis - 19 Oct, 2021. Quantum Physics of Information
- Eduardo Testé, UCSB - 12 Oct, 2021. Mutual information superadditivity and unitarity bounds
- Djordje Racidevic, Brandeis - 4 Oct, 2021. An Introduction to the Lattice-Continuum Correspondence
- Juan Pedraza, University of Barcelona - 27 Sep, 2021. Lorentzian threads and holographic complexity
- Etera Livine, ENS Lyon - May 17th, 2021. Bulk-boundary in loop quantum gravity
- Ana Alonso-Serrano, AEI Potsdam - April 12th, 2021. Quantum gravity phenomenology from thermodynamics of spacetime
7. Other
Nothing to report.