Informational reconstruction of quantum theory
Fields: quantum foundations, quantum information
Quantum theory has enjoyed an outstanding success, allowing us to make precise predictions about the physical microcosm, leading to new information technologies and withstanding every experimental test to which it has been exposed thus far. Yet, in contrast to special and general relativity, quantum theory has evaded a commonly accepted apprehension and interpretation of its physical content, in part as a consequence of a lack of physical statements that fully characterize it. But, what makes quantum theory special? Quantum theory has perhaps become so successful that questioning its foundations and physical content have become peripheral matters in physics. However, with the ambition of developing more fundamental theories, involving or going beyond quantum theory, the question as regards its physical meaning and characterizing features returns. Furthermore, a convincing conceptual scheme for a putative quantum theory of gravity presumably requires a deeper understanding of what quantum theory tells us about Nature, and of what we can say about it.
Why should the world be described in terms of complex Hilbert spaces, operators, tensor product rules, unitary evolution, etc., rather than some other mathematical structures? How could the world be different if we dropped or modified some of quantum theory's characterizing features? Questions along these lines are epitomized by Wheeler's "how come the quantum?". Answering these questions requires a better understanding of quantum theory within a large landscape of alternative theories, which do not presuppose the formalism of quantum theory, but are instead formulated in terms of a more general operational language, namely in terms of probabilities. Various such reconstructions appeared in the literature in the past twenty years.
In order to provide a possible answer to Wheeler's question, we developed an informational reconstruction of quantum theory, which derives its formalism from elementary rules constraining an observer's acquisition of information from physical systems. The acquisition of information of the observer O about the systems S proceeds by interrogation with binary questions.
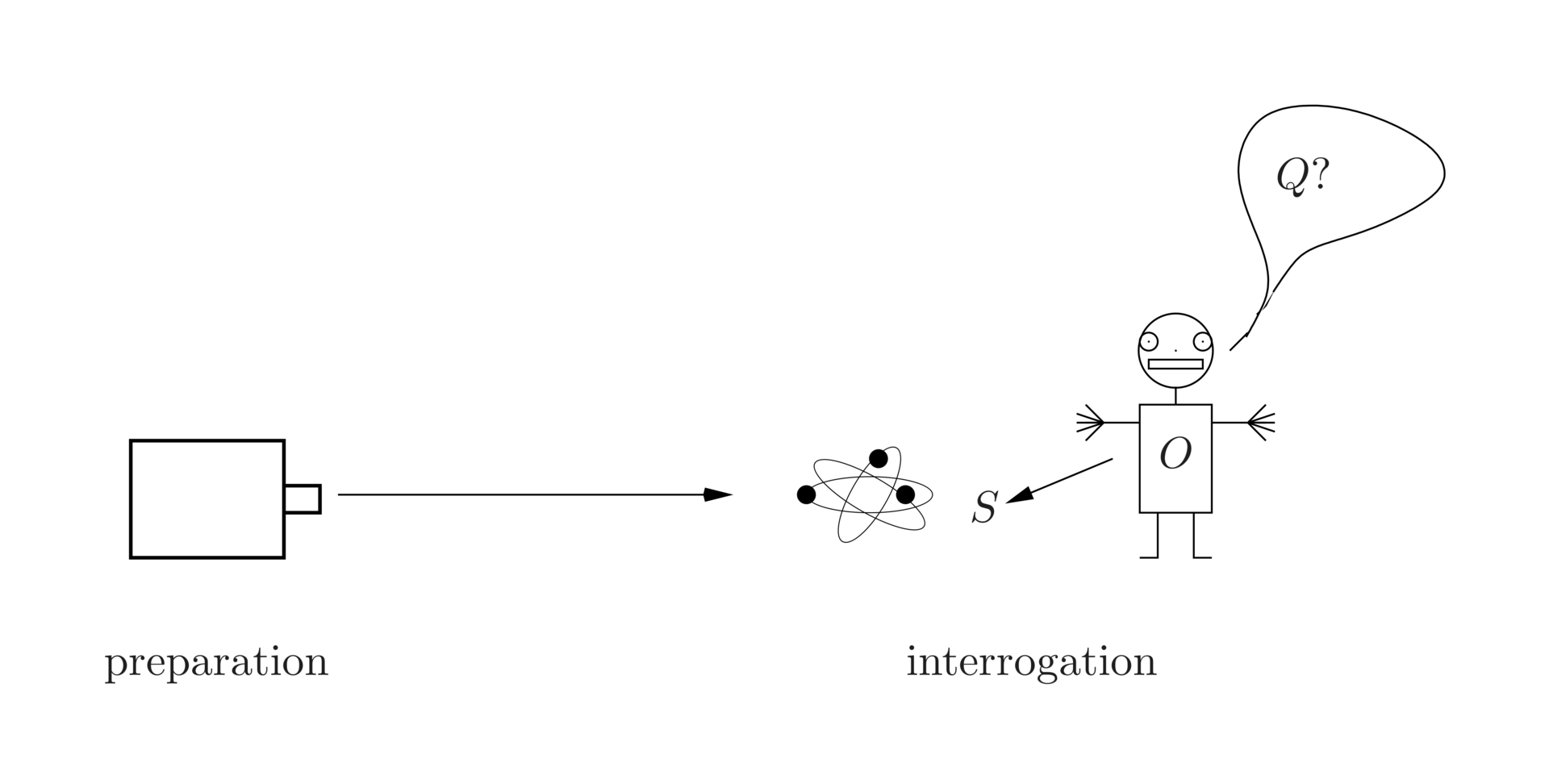
Colloquially, the rules giving rise to the quantum formalism of N qubits are the following:
Limited information: O can maximally acquire N independent bits of information about S at any time.
Complementarity: O can always get up to N new independent bits of information about S without changing the total amount of information they hold about S.
Information preservation: O’s total amount of information about S is preserved in-between interrogations.
Time evolution: O’s catalog of knowledge of S changes continuously in time and every consistent such evolution is physically realizable.
Question unrestrictedness: O can ask S any binary question that “makes sense.”
These five axioms have two "solutions": (1) the formalism of N qubits in standard complex quantum theory, and (2) the formalism of N two-level systems in quantum theory over real Hilbert spaces (rebits). The following additional axiom finally precludes the rebit case, leaving standard quantum theory as the sole survivor:
Tomographic locality: If S is a composite system, O can determine its state by interrogating only its subsystems.
This reconstruction provides an informational explanation for the structure of quantum theory and especially for its paradigmatic features such as entanglement, monogamy and non-locality. It also produced new structural insights, unraveling `conserved informational charges' from complementarity relations that characterize the unitary group and the set of pure states.
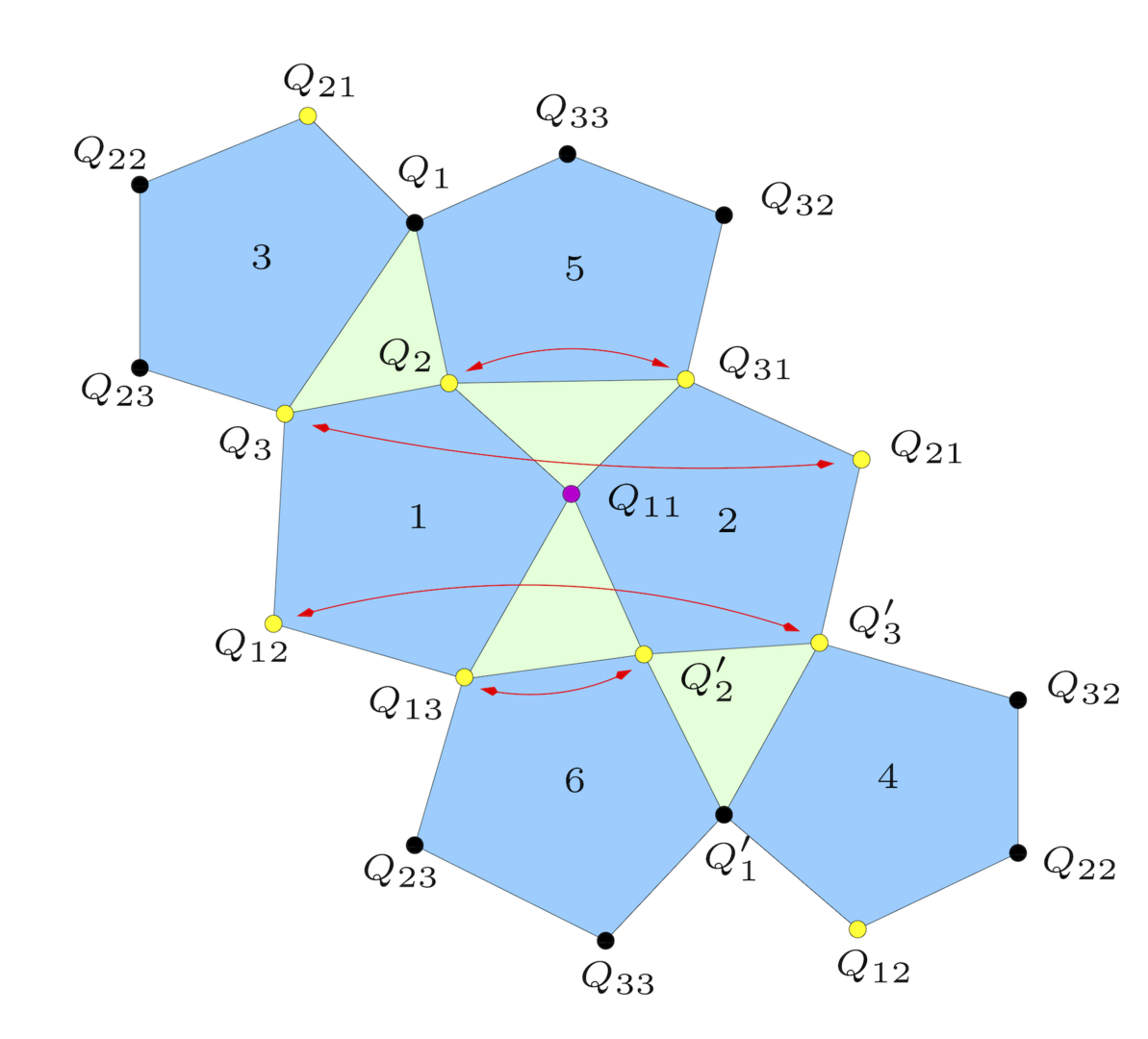
Complementarity relations for the 15 independent binary questions (projectors onto +1 eigenspaces of Pauli operators) of two qubits, reconstructed through the limited information and complementarity rules. The red arrows represent an 'information swap' that leaves certain 'informational charges' invariant and corresponds to a generator of PSU(4), the projective unitary group of time evolutions of two-qubit density matrices.
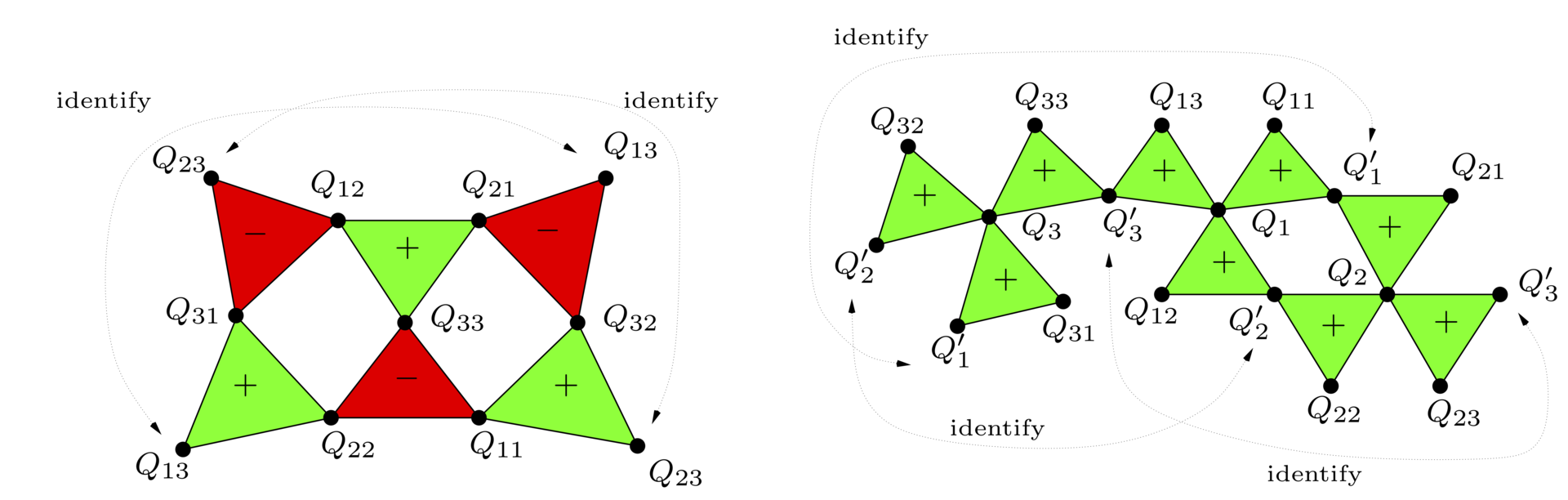
The correlation structure of two-qubits, reconstructed using the limited information and complementarity rules.
Further reading:
- P. A. Höhn 2017, "Toolbox for reconstructing quantum theory from rules on information acquisition", Quantum 1 38, https://doi.org/10.22331/q-2017-12-14-38 (Preprint arXiv:1412.8323)
- P. A. Höhn and C. Wever 2017, "Quantum theory from questions", Phys. Rev. A 95 012102, https://doi.org/10.1103/PhysRevA.95.012102 (Preprint arXiv:1511.01130)
- P. A. Höhn 2017, "Quantum theory from rules on information acquisition", Entropy 19(3) 98, https://doi.org/10.3390/e19030098 (invited contribution to the special issue "Quantum information and foundations", Eds. D'Ariano and Perinotti, Preprint arXiv:1612.06849)
- P. A. Höhn 2017, "Reflections on the information paradigm in quantum and gravitational physics", J. Phys. Conf. Ser. 880 012014, https://doi.org/10.1088/1742-6596/880/1/012014 (invited contribution to DICE Proceedings, Ed. H.-T. Elze, Preprint arXiv:1706.06882)



