Evolving phase and Hilbert spaces for discrete gravity and lattice field theory
Fields: classical and quantum gravity, lattice field theory, discrete mechanics, variational integrators, mathematical physics
Evolving discretizations arise generically in discrete (quantum) gravity models and in field theory on an evolving lattice. Understanding these discretization changing dynamics is a challenge in quantum gravity and, for example, applies to loop quantum gravity.
We devised the first comprehensive framework for describing these evolving discretizations, which works quite differently than in the continuum. To cope with the varying number of degrees of freedom, we developed the concepts of evolving phase and Hilbert spaces and a systematic constraint analysis thereon. We clarified the notion of symmetries, Dirac (i.e. gauge-invariant) observables, and physical phase and Hilbert spaces for evolving lattice systems and elucidated in which sense a discretization changing dynamics can or cannot be symplectic or unitary. This also includes a complete classification of constraints and degrees of freedom, incl. coarse graining or refining constraints.
The framework has so far been applied to Regge Calculus, the most well-known discretization of general relativity, and scalar lattice field theories. It provides the canonical formulation of Regge Calculus and leads to an elegant scheme for counting lattice gravitons in the evolving triangulation in terms of so-called Pachner moves.
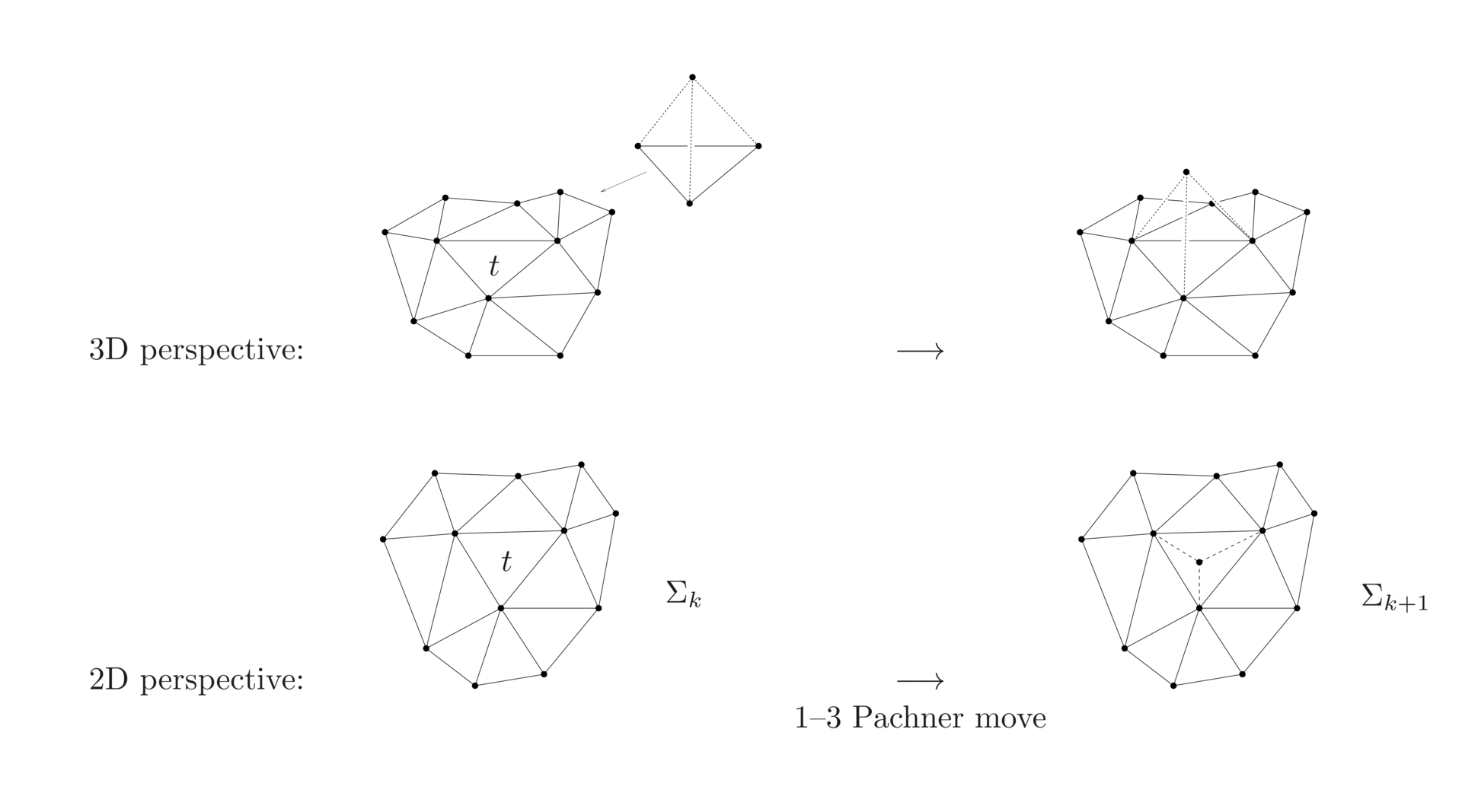
Gluing a tetrahedron onto a single triangle in a 2D triangulated hypersurface (bounding some 3D bulk triangulation) is equivalent to a so-called 1-3 Pachner move in the 2D hypersurface. Pachner moves are an elementary class of moves (they only involve a fixed number of simplices) which are ergodic piecewise linear homeomorphisms (one can map between any finite triangulations of the same topology by finite sequences of these moves).
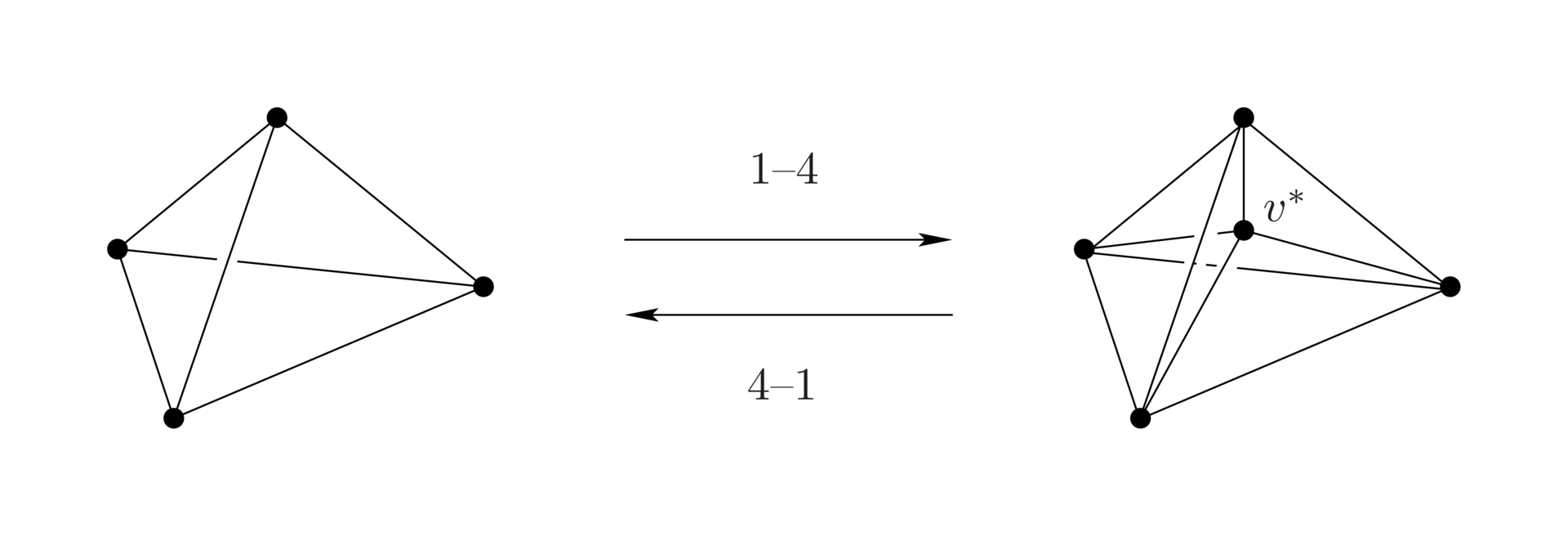
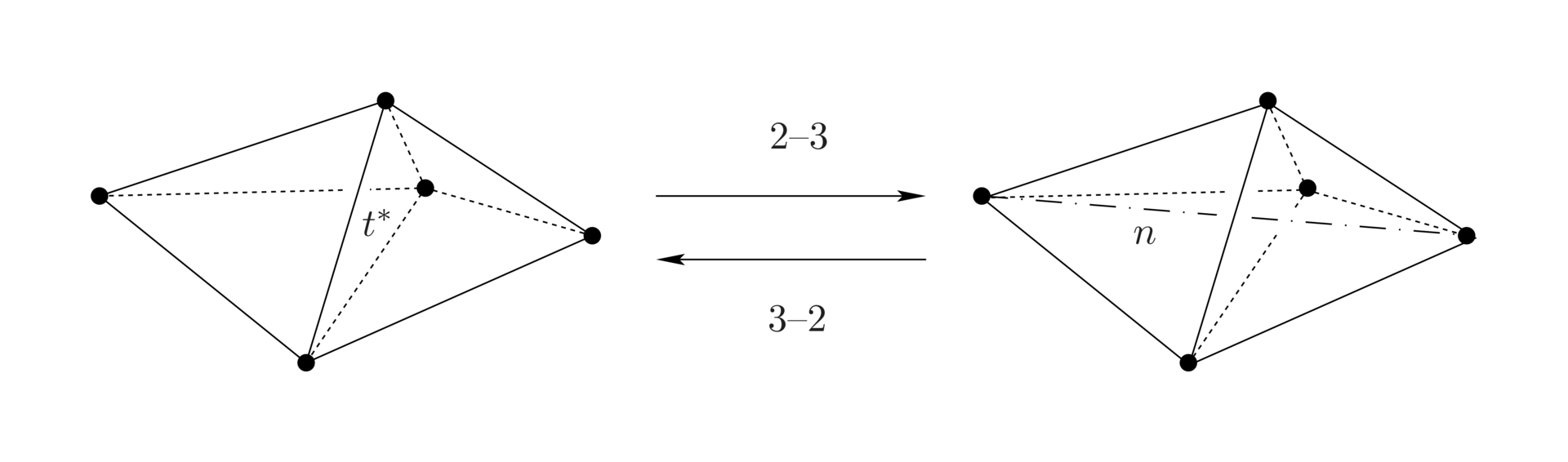

Further reading:
- P. A. Höhn 2015, "Canonical linearized Regge calculus: Counting lattice gravitons with Pachner moves", Phys. Rev. D 91 124034, https://doi.org/10.1103/PhysRevD.91.124034 (Preprint arXiv:1411.5672)
- P. A. Höhn 2014, "Classification of constraints and degrees of freedom for quadratic discrete actions", J. Math. Phys. 55 113506, https://doi.org/10.1063/1.4900926 (Preprint arXiv:1407.6641)
- P. A. Höhn 2014, "Quantization of systems with temporally varying discretization II: Local evolution moves", J. Math. Phys. 55 103507, https://doi.org/10.1063/1.4898764 (Editor's Picks 2014, Preprint arXiv:1401.7731)
- P. A. Höhn 2014, "Quantization of systems with temporally varying discretization I: Evolving Hilbert spaces", J. Math. Phys. 55 083508, https://doi.org/10.1063/1.4890558 (Editor's Picks 2014, Preprint arXiv:1401.6062)
- B. Dittrich and P. A. Höhn 2013, "Constraint analysis for variational discrete systems," J. Math. Phys. 54 093505, https://doi.org/10.1063/1.4818895 (Preprint arXiv:1303.4294)
- B. Dittrich and P. A. Höhn 2012, "Canonical simplicial gravity", Class. Quant. Grav. 29 115009, https://doi.org/10.1088/0264-9381/29/11/115009 (Preprint arXiv:1108.1974)
- B. Dittrich and P. A. Höhn 2010, "From covariant to canonical formulations of discrete gravity", Class. Quant. Grav. 27 155001, https://doi.org/10.1088/0264-9381/27/15/155001 (Preprint arXiv:0912.1817,)



