Annual Report 2014
Neural Computation Unit
Professor Kenji Doya

Abstract
1. Staff
Dynamical Systems Group
- Junichiro Yoshimoto, Group Leader
- Jun Igarashi, Staff Scientist
- Ildefons Magrans de Abril, Staff Scientist
- Jan Moren, Staff Scientist
- Osamu Shouno, Visiting researcher
- Naoto Yukinawa, Staff Scientist
- Jessica Verena Schulze, OIST Student
- Kosuke Yoshida, Special Research Student
Systems Neurobiology Group
- Makoto Ito, Group Leader
- Akihiro Funamizu, Postdoctoral Scholar
- Kazumi Kasahara, JSPS Research Fellow
- Katsuhiko Miyazaki, Staff Scientist
- Kayoko Miyazaki, Staff Scientist
- Yu Shimizu, Staff Scientist
- Tomoki Tokuda, Postdoctoral Scholar
- Hiroaki Hamada, OIST Student
- Tomohiko Yoshizawa, Special Research Student
Adaptive Systems Group
- Eiji Uchibe, Group Leader
- Stefan Elfwing, Researcher
- Qiong Huang, OIST Student
- Shoko Igarashi, OIST Student
- Farzana Rahman, OIST Student
- Chris Reinke, OIST Student
- Jiexin Wang, Special Research Student
Administrative Assistant / Secretary
- Emiko Asato
- Kikuko Matsuo
2. Collaborations
- Theme: The research of biologically-inspired reinforcement learning systems for human-centered interface intelligence of future machines
- Type of collaboration: Joint research
- Researcher(s):
- Osamu Shouno, Honda Research Institute Japan Co., Ltd
3. Activities and Findings
3.1 Dynamical Systems Group
3.1.1 Large-scale spiking neuron models of the basal ganglia-thalamo-cortical circuit [Moren, Igarashi, Shouno, Yoshimoto]
The basal ganglia are the locus of Parkinson's disease and the basal ganglia-thalamo-cortical circuit is known to play a critical role in the development of tremor and other motor-related symptoms. However, the precise mechanism for the loss of dopaminergic projection to the basal ganglia circuit to cause Parkinsonian tremor is still unknown. To understanding the dynamic circuit mechanisms of Parkinsonian pathology, we constructed an integrated model of the basal ganglia-thalamo-cortical circuit.
We first constructed a spiking neural network model of the STN-GPe circuit, a subset of the basal ganglia circuit, and found that post-inhibitory rebound potentiation of STN neurons and short-term synaptic plasticity of GPe neurons can cause pathological oscillatory burst activities in the frequencies range of 8-30 Hz. We then developed a model of thalamo-cortical circuit, which receives input from basal ganglia and sends motor command signal to the spinal cord. In the simulations, the motor cortex showed alternating activation of separate neural populations due to lateral inhibition. The model of the whole thalamo-cortical circuit exhibited oscillatory neural activity in the theta (4-8 Hz) and alpha (8-14 Hz) frequency ranges, which may cause oscillatory movements in healthy subjects and Parkinson’s patients.
We further made the thalamo-cortical model more realistic by introducing spatial features (e.g. layer thickness and cell density) based on the anatomical data (Igarashi et al., 2014), and ran simulations to test whether the model reproduces neural activities observed in Parkinson’s disease tremor. When we set relatively strong inhibitory bias current to thalamo-cortical cells, spatial clusters of thalamo-cortical cells showed simultaneous burst firing due to lateral inhibition by thalamic reticular neurons and thalamic interneurons. Anti-phase synchronization also occurred among the spatial clusters. While thalamo-cortical neurons and layer 5B pyramidal tract neurons showed burst firing at about 5-6 Hz, the population firing of these neurons oscillated at a double frequency of about 10-12 Hz, due to anti-phase synchronization of the 5-6 oscillations. These simulation results reproduced the experimental observations of anti-phase synchronization of EMGs and the entrainment of EMG oscillation to alpha range oscillation in M1.
3.1.2 Subtype identification and diagnosis of depression from multidimensional data using machine learning [Shimizu, Tokuda, Yoshida, Yoshimoto]
Diagnosis of depression is currently based on long interviews. In the search for an objective and more efficient method to diagnose this complex disease we analyze multidimensional data, including structural magnetic resonance imaging (MRI) data, functional MRI data involving four different tasks, resting state data, as well as blood markers, genetic polymorphism and behavioral tests, obtained from (currently 130) depression patients and (currently 120) healthy controls using machine learning algorithms. We investigate how subtypes can be identified and how they can be categorized so as to provide a basis for adequate treatment methods.
In the beginning of this fiscal year we published last year’s results in the paper “Toward Probabilistic Diagnosis and Understanding of Depression Based on Functional MRI Data Analysis with Logistic Group LASSO” in the journal PLOS One.
In the following months, we used L1 version of the LASSO approach to diagnose patients and predict the chance of recovery after treatment with selective serotonin uptake inhibitor (SSRI), from their behavior data, blood markers, genetic information and relative white and gray brain matter. For the diagnosis prediction model we used data from 37 patients (age 39.78+/-10.66, 17 male) and 37 patients (age 38.35+/-10.70, 19 male). Among the patients 23 showed 50% lower depression scores (measure in HRSD) 6 weeks after SSRI treatment than when first admitted to hospital, indicating recovery from depression. The remaining 19 were considered as non-responsive to therapy.
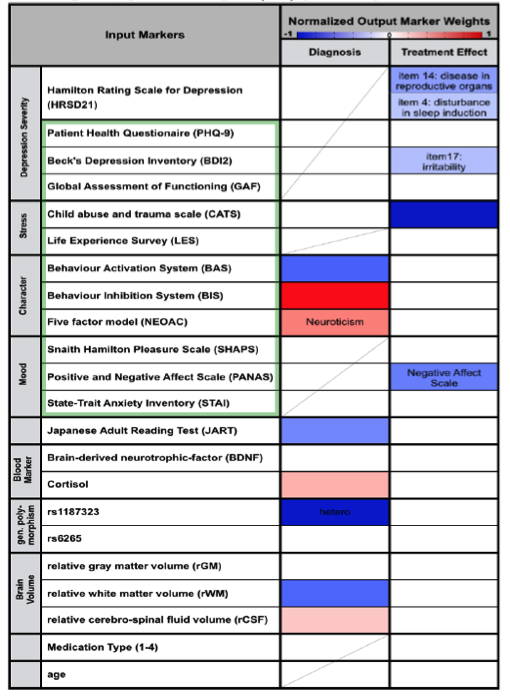
The data used as input to the regression algorithm consisted in results from depression related assessment test (Table 2, green frame), reading performance (JART), the phenotypes of two depression related genes (rs1187323, rs6265), blood markers (blood BDNF and Cortisol level) and relative white matter, gray matter and cerebrospinal fluid volume. While symptom severity measures such as PHQ-9 and BDI2 were excluded in the estimation of the diagnosis model in order to reveal other factors characteristic for depression, 21 items describing the symptom severity according to the Hamilton Rating Scale for Depression (HRSD21) and the prescribed medication were added in the estimation of the treatment response prediction model.
In order to account for the different modalities of the input markers, continuous values were normalized by subtraction of the mean and division through the standard deviation. Integer valued data was transformed by taking the square root and normalized thereafter. Binary valued data is normalized by default and were left unchanged.
Verified through 10-fold nested cross validation a diagnosis accuracy of 75±3% could be achieved (sensitivity: : 73±4%, specificity: 77±4%, Table 1). Thereby the markers indicating healthy controls (negative regression weights) were Genotype, Behavior activation system, relative white matter volume and reading abilities (Table2). Positive weight markers (indicating depression) were Behavior Inhibition System, Neuroticism, Cortisol level and relative CSF volume. Prediction of treatment response could be accomplished with an accuracy of 75±4% (sensitivity: 81±5%, specificity: 65±7%). No specific weights pointing towards good chance of recovery were found, however negative weights were found indicating no treatment response for patients with high child abuse experience (CATS), negative affect scale (PANAS_N) and specific HRSD and BDI2 items (Table2).
Table 1: Classification Performance (mean ± std over 100 10-fold cross validations)
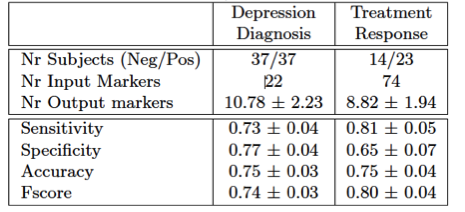
Table 2: Weight of behavioral traits and biomarkers for depression diagnosis and investigation of treatment effect. Negative weights (blue) promote negative, positive weights (red) promote positive labels.
In the field of unsupervised learning, we developed a novel co-clustering method, which is applicable to a dataset consisting of numerical and categorical features. This method first partitions features in a data-driven way, and then carries out co-clustering (clustering both samples and features) using specific sets of features. In a nutshell, this method allows us to identify multiple sample-clustering solutions using their relevant set of features.
We applied this method to depression data collected at Hiroshima University, which consists of clinical questionnaires on depression severity, bio-markers, and functional MRI (data size 134 subjects × 2948 features). As a result, 15 co-clustering solutions were identified. Among these solutions, we analyzed more in depth the most relevant co-clustering solution to the label of control and depression. It was found that in this co-clustering solution, there were two control sub-clusters, and three depression sub-clusters. Further, these depression sub-clusters were characterized by the following features: depression severity indices taken 6 weeks and 6 months after the onset of the treatment; indices on child abuse experiences in subject’s childhood; 13 functional connectivity in the functional MRI data. These features enabled us to characterize the three depression sub-clusters as follows: 1) Less child abuse experiences and remission; 2) High child abuse experiences and remission; 3) High child abuse experiences and non-remission. Furthermore, it was found that the relevant brain areas to the aforementioned 13 functional connectivity were in the default-mode network. In particular, the left angular gyrus played the role of ‘hub’ in these relevant brain areas. Practically, these results imply a possibility that we may predict effect of the anti-depression drug before the start of the treatment, based on child abuse experiences and functional connectivity in these relevant brain areas.
3.1.3 Multiscale modeling of of dopaminergic actions on basal ganglia network: From neurons to behavior [Yukinawa, Yoshimoto]
In this fiscal year, we aimed to construct solid computational bases for simulating and visualizing neurobiological mechanism of action modification through striatal intracellular phosphosignaling triggered by dopamine and adenosine. For this purpose we conducted 1) further extensions of kinetic signal transduction models for synaptic plasticity in D1R- and D2R-expressing medium spiny neurons (D1R and D2R-MSNs) based on the last year’s development and 2) simulation of action selection based on response of a macroscopic circuit model of cortico-basal ganglia pathway.
1) Extensions of kinetic signal transduction models for synaptic plasticity of striatal medium spiny neurons
We had been constructing basic kinetic signal transduction models of medium spiny neurons which include dopamine and adenosine pathways and also validating their plausibility by collaborating with an experimental research group (Prof. Dr. Kaibuchi of Nagoya University) in the previous fiscal years. Fundamental signaling components of the models include phosphorylation of glutamate receptor subunit GluR1 (Ser845) by PKA-DARPP32 pathways, Rap1/MAPK activation pathway by PKA-dependent phosphorylation of Rap1GAP, and phosphorylation of cofilin, which contribute to cellular excitation and long-term synaptic plasticity induced by AMPA receptor trafficking and spine enlargement. On the basis of these previous development, in this fiscal year, we tried to improve biological plausibility of the models and consistency between model prediction and experimental data about dynamics of phosphosignaling by introducing a model of permeation delay process of extracellular signals into cellular tissue, D2R-MSN specific signal transduction pathways, and simple multi-compartmentalization of the biochemical reaction space assuming spine morphology. We describe each details as follows.
In the model validation during last fiscal year, we had compared simulated and experimental results of phosphoresponses of D1R-/D2R-MSNs induced by D1R or A2AR agonists. There we found that the steady-state behaviors are consistent between simulation and experiments but there is a major discrepancy with respect to the dynamic time-courses. In particular the experimental data shows the peak phosphoresponses in order of minutes while the simulation predicted those in order of around ten seconds; this indicates that there exists clear difference in the reaction time constants. The reasons may be that it requires certain time for receptor agonists to perfuse effectively into striatal slice preparations and also that the slice preparations are actually mixture of both D1R- and D2R-MSNs, which could weaken signaling efficacy of agonists. We took into account the former possibility and modeled a permeation process of agonist solution into the cell slice preparations by considering a one-dimensional diffusion process. The model is simple enough to be fitted by data, thanks to a single joint parameter with respect to ratio between diffusion constant and slice thickness. We incorporated it into the kinetic signal transduction models of MSNs and estimated the model parameter and effective agonist concentration by using experimentally obtained time-course data about phosphoresponse of DARPP-32 (Thr34) and GluR1 (Ser845) triggered by 5 μM CGS21680, an A2AR agonist solution (Fig. 3.1.1A and 3.1.1B, here we just show the results of GluR1). We then applied the fitted model to predict CGS21680 dose-responses at 120 seconds after onset (Fig. 3.1.1C). The results show that the kinetic signal transduction model with agonist permeation process improves simulation reproducibility for experimental results.
Then we explored and introduced additional D2R-MSN specific signal transduction mechanism into the kinetic signal transduction model of D2R-MSN. In D2R-MSN, some portion of D2Rs bind to Gq protein which regulates phospholipase C (PLC) while most D2Rs engages in the PKA inhibition pathway. The D2R-Gq-PLC pathway is another fundamental pathway contributing to the cellular excitability because diacyl glycerol (DAG) and inositol triphosphate (IP3), which are hosphatidylinositol 4,5-bisphosphatase (PIP2) hydrolyzates by PLC, regulate downstream phosphorylation pathways via PKC activation and intracellular calcium signaling, respectively (Surmeier et al., Trends Neurosci, 2007). We here developed model components including hydrolysis of PIP2 into DAG and PIP2 and PKC activation by DAG based on previous modeling works (Fig. 3.1.2). These additional components enabled us to simulate further detailed physiological dynamics of D2R-MSN including conductance inhibition by PKC phosphorylation of Nav 1.1 and coordinated action of intracellular calcium dynamics and A2AR/D2R-AC5-PKA pathway for synaptic plasticity.
For the multi-compartmentalization of signal transduction model considering spine morphology, we then developed a simple kinetic model assuming molecular diffusion between spine body and head compartments. Specifically, we modeled it as delay due to membrane trafficking of phosphorylated AMPAR. By using the model, we predicted that time courses for concentrations of membrane inserted AMPAR and activated cofilin are highly correlated (Fig. 3.1.3). The model may help us to investigating detailed spatiotemporal profiles between AMPAR accumulation in the spine head and volumetric changes of dendritic spine by cytoskeletal reorganization which are major components of synaptic plasticity in the MSNs.
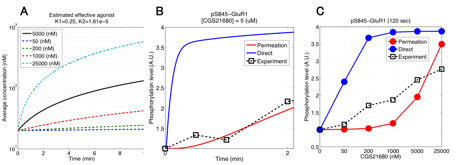
Figure 3.1.1: Model-based prediction of A2AR-stimulated phosphoresponse with permeation of agonists into slice preparations. (A) Time course of estimated effective concentration in a slice preparation of CGS21680. (B) Simulated traces of phosphorylation of GluR1 (Ser845). Blue and red lines are the simulated phosphoresponses by the original kinetic signal transduction model and by the model with assumption of permeation delay of CGS21680 solution, respectively. Black squares are experimental observations. (c) CGS21680 dose-response curves for six different agonist concentrations.
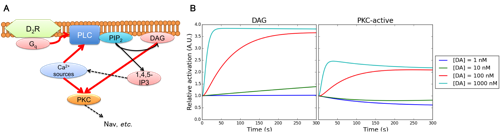
Figure 3.1.2: Model-based prediction of A2AR-stimulated phosphoresponse with permeation of agonists into slice preparations. (A) Time course of estimated effective concentration in a slice preparation of CGS21680. (B) Simulated traces of phosphorylation of GluR1 (Ser845). Blue and red lines are the simulated phosphoresponses by the original kinetic signal transduction model and by the model with assumption of permeation delay of CGS21680 solution, respectively. Black squares are experimental observations. (c) CGS21680 dose-response curves for six different agonist concentrations.
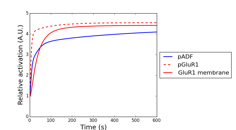
Figure 3.1.3: Simulated phosphorylation profiles of synaptic plasticity related proteins by using AMPAR trafficking model. Red, red dashed, and blue lines represent relative concentration of membrane trafficked GluR1, intracellular GluR1, and phosphorylated cofilin, respectively.
2) Modeling action selection based on a macroscopic cortico-basal ganglia circuit response
Our primary goal of this research topic is to simulate detailed single cellular level changes in excitability of the MSNs and also circuit level activity of the cortico-basal ganglia system, which are regulated by pharmacological actions of dopamine and adenosine. For these purpose, we first developed a detailed electrophysiological model which consists of several conductance of MSN-specific ion channels by incorporating dopamine-dependent modulation of a potassium channel KCNQ2. We also conducted an integrated simulation by coupling it and the kinetic signal transduction model which we described in the previous section. We then developed a simple action selection model of the basis of circuit level activities of macroscopic anatomy of the cortico-basal ganglia system. We describe the details of each model below.
Our experimental collaborators showed that phosphorylation of Rap1GAP, which is one of key signaling molecule of PKA downstream, substantially contributes to cocaine-induced excitability changes of D1R-MSN (Nagai, et al., Neuron, in revision), where the phosphorylation of Rap1GAP disinhibits further downstream pathways by activating several kinases including CaMKII, MEK, and ERK. However, so far, they have not examined which ion channels are major correlates of the intrinsic electrophysiological excitability, while KCNQ2 is a novel potential candidate because a mass spectrometry-based analysis revlealed its DA-dependent phosphorylation. In order to estimate potential contribution of KCNQ2 current for the excitability we developed a detailed conductance-based electrophysiological model including mechanism of KCNQ2 and other principal ion channels in D1R-MSN (Fig 3.14A). The model is a single compartment reduction of a previous modeling work by Moyer et al. (J Neurophysiol, 2007) with additional KCNQ2 modulation where we hypothesized that DA-dependent phosphorylation of KCNQ2 inactivates the current. We simulated electrophysiological activity in current-clamp experiments by using the model and showed that decrease of KCNQ2 current largely contributes to excitation of D1R-MSN (Fig. 3.1.4B). The results are consistent with experimental observations by using slices of mouse nucleus accumbens with genetic modification of Rap1GAP, thus suggesting that Rap1-mediated KCNQ2 modulation is a fundamental biological component for DA-dependent excitability regulation of D1R-MSN.
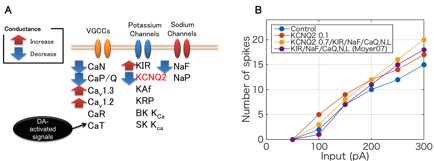
Figure 3.1.4: Electrophysiological model of the D1R MSN with KCNQ2 current. (A) All ion channels in the model and DA-dependent actions on them. (B) Predicted firing frequency of the model considering several modulation assumptions for different current inputs (800 ms).
We then conducted preliminary simulation of integration of intracellular signal transduction and electrophysiology of D1R-MSN in order to quantitatively investigate coordinated actions of dopamine-dependent excitability modulation in single cellular level. We employed PhysioDesigner software (http://www.physiodesigner.org) as a modeling and coordinator environment to combine the signal transduction model and the conductance-based electrophysiological model described above. In the integrated simulation, each model mutually exchanges information of intracellular calcium and extracellular dopamine concentrations directly while phosphorylated GluR1 and ERK concentrations in the signal transduction model are converted into AMPAR conductance and conductance parameters of several ion channels in the electrophysiological model, respectively. We simulated cellular responses under conditions in which constant somatic current injection and D1R agonist are applied to D1R-MSN simultaneously and confirmed that the pharmacological dopamine signal leads to electrophysiological activation via the intracellular signaling cascades in a bottom-up manner (Fig. 3.1.5).
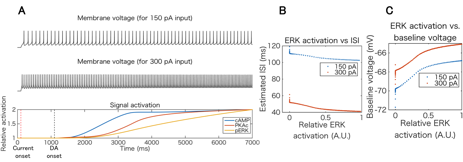
Figure 3.1.5: Integrated simulation of intracellular signal transduction and electrophysiology of D1R-MSN. (A) Top and middle plots show simulated voltage traces for different current injections (150 pA and 300 pA, respectively), and bottom plot is time course of relative activation of key signaling molecules including cAMP, PKA, and ERK. (B) and (C) Inter spike interval and baseline voltage changes versus active ERK level.
Next, we constructed a macroscopic circuit level model of the cortico-basal ganglia system to investigate pharmacological action of dopamine and adenosine signals on emotional behavior of animals. The model consists of minimal but fundamental brain regions of the direct and indirect pathways including cortex, nucleus accumbens (NAc), subthalamic nucleus (STN), external globus pallidus (GPe), and substantia nigra pars reticulata (SNr). Each brain region is represented by neural population and connected to other regions according to basic anatomical structure of the cortico-basal ganglia networks. We assume internal state of each region is represented by mean firing rate of the population whose dynamics is described by a simple leaky integrator. Output of each region is obtained by applying piecewise linear activation function to the internal state, where modulation effect of agonists/antagonists to D1R, D2R, and A2AR, which are predicted by the cellular scale models of MSNs described previously, are introduced by modifying the gradient coefficient parameters of NAc populations. We define the inverse activation of SNr population with a certain threshold as tendencies to take action. We applied the model to simulate dopamine and adenosine-dependent changes in motivational behavior assuming intracranial self-stimulation experiments with mice. We first predicted modulation effect on behavioral frequency in cases of indirect pathway specific manipulation by controlling A2AR signals (Fig. 3.1.6A). The results show that A2AR agonists decrease net sensitivity to reward (dopamine) inputs while the antagonists facilitate it. We then investigated therapeutic contributions of A2AR antagonists to the Parkinson’s disease by simulating tonic dopamine depletion states in NAc (Fig. 3.1.6B). The results show, in low dopamine conditions, that sensitivity to reward decreases due to inactivation of both direct and indirect pathways; however, application of A2AR antagonists partially reverts the sensitivity by inhibiting NAc population which consists of D2R-MSNs.
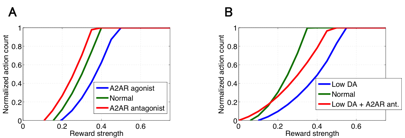
Figure 3.1.6: Simulated behavioral modulation in several pharmacological settings by the using circuit level model of cortico-basal ganglia pathways. In each panel, horizontal and vertical axes represent applied reward strength and behavioral frequency, respectively. (A) Action modulation induced by A2AR agonist (blue line) and antagonist (red line). (B) Simulated Parkinsonian state (blue line) and the relieved state by A2AR antagonist (red line).
3.1.4 Development of a neuroinformatics platform for protein phosphorylation with quality control [Yoshimoto]
Protein phosphorylation is involved in the regulation of a wide variety of physiological processes in the nervous system. Thanks to recent developments in proteomics and genomics, it is predicted that the number of protein kinases and phosphorylated sites in human proteins amounts to approximately 500 and 650,000, respectively. On the other hand, little is known about which sites are phosphorylated by a specific kinase and which extracellular stimuli activate (or inhibit) the protein phosphorylation via intracellular signaling cascades. To uncover the basic issue, Prof. Kozo Kaibuchi (Nagoya University Graduate School of Medicine) and collegues recently developed a new methodology for screening the target phospholyrated sites of a given kinase using the mass spectrometry, and succeeded in identifying hundreds of phosphorylated sites of representative kinases such as PKA, MAPK, CaMKII and so on. To summarize the data systematically and extract biologically significant information, we developed a database system named KANPHOS (Kinase-Associated Neural Phospho-Signaling).
The database system and its web portal were built based on XooNIps (http://xoonips.sourceforge.jp). As of April 2015, about 8,300 pairs of protein kinases and phosphorylated sites identified by our method, as well as about 4,000 pairs cited from the literature, have been registered in the database. All data are controlled for quality via review and curation by specialists. The web portal supports three modes of search: 1) Search for substrates phosphorylated by a specific kinase; 2) Search for kinases phosphorylating a specific protein; and 3) Search for kinases and their target substrates by a specific signaling pathway. Each protein (kinase/substrate) item is linked with external databases such as Uniprot KB (proteomics database), HGNC DB (human genomics database), HuGE Navigator (human genome epidemiology database), and Allen Brain Atlas, enabling us to easily predict unknown functions of the protein phosphorylation. As an advanced option, we also implemented a function to show a list of pathways in which the set of substrates phosphorylated by a specific condition is overrepresented more than expected, via communication with Reactome (http://www.reactome.org). Using this function, we estimate proteins and pathways in striatal medium-sized spiny neurons modulated by extracellular dopaminergic stimulation.
3.2 Systems Neurobiology Group
3.2.1 The role of serotonin in the regulation of patience [Katsuhiko Miyazaki, Kayoko Miyazaki]
While serotonin is well known to be involved in a variety of psychiatric disorders including depression, schizophrenia, autism, and impulsivity, its role in the normal brain is far from clear despite abundant pharmacology and genetic studies. From the viewpoint of reinforcement learning, we earlier proposed that an important role of serotonin is to regulate the temporal discounting parameter that controls how far future outcome an animal should take into account in making a decision (Doya, Neural Netw, 2002).
In order to clarify the role of serotonin in natural behaviors, we performed neural recording, microdialysis measurement and optogenetic manipulation of serotonin neural activity from the dorsal raphe nucleus (DRN), the major source of serotonergic projection to the cortex and the basal ganglia.
So far, we found that the level of serotonin release was significantly elevated when rats performed a task working for delayed rewards compared with for immediate reward (Miyazaki et al., Eur J Neurosci, 2011). We also found many serotonin neurons in the dorsal raphe nucleus increased firing rate while the rat stayed at the food or water dispenser in expectation of reward delivery (Miyazaki et al., J Neurosci, 2011).
To examine causal relationship between waiting behavior for delayed rewards and serotonin neural activity, 5-HT1A agonist, 8-OH-DPAT was directly injected into the dorsal raphe nucleus to reduce serotonin neural activity by reverse dialysis method. We found that 8-OH-DPAT treatment significantly could not wait for long delayed reward (Miyazaki et al., J Neurosci, 2012). These results suggest that activation of dorsal raphe serotonin neurons is necessary for waiting for delayed rewards.
To further investigate whether a timely activation of the DRN serotonergic neurons causes animals to be more patient for delayed rewards, we introduced transgenic mice that expressed the channelrhodopsin-2 variant ChR2(C128S) in the serotonin neurons. We found that serotonin neuron stimulation prolonged the time animals spent for waiting in reward omission trials. This effect was observed specifically when the animal was engaged in deciding whether to keep waiting and not due to motor inhibition. Control experiments showed that the prolonged waiting times observed with optogenetic stimulation were not due to behavioral inhibition or the reinforcing effects of serotonergic activation (Miyazaki et al., Curr Biol, 2014). We also found that serotonin activation did not change lever pressing behavior when animals required more effort to get rewards. These results established a causal relationship between serotonin neural activation and patient waiting for future rewards.
3.2.2 Dissociation of working memory-based and value-based strategies in a free-choice task [Makoto Ito, Tomohiko Yoshizawa]
While value-based reinforcement learning (RL) algorithms have well explained strategies and neuronal basis of decision making, few studies have focused on how working memory (WM) influences choice strategies. In this study, we investigated whether and how rats’ choice strategy was affected by interference of WM and examined relevant neuronal activities in the primary motor cortex (M1), the dorsolateral striatum (DLS), the prelimbic cortex (PL) and the dorsomedial striatum (DMS).
We trained rats to perform a choice task with controlled interference of WM. The task was started by a presentation of “choice tone” or “no-choice tone”. After choice tone, a rat was required to perform a nose poke into ether left or right hole (choice trials), then a food pellet was delivered probabilistically depending on the choice. The reward probabilities were reversed after several tens of choice trials. For no-choice tone, rat was required not to perform any nose pokes (no-choice trials). In the interference condition (IC), no-choice trial was inserted after every choice trial, and the consecutive condition (CC) consisted of only choice trials.
In behavioral analysis, we calculated proportions of how often the rats repeated the same actions after rewarded trials (win-stay) and chose the other actions after no-rewarded trials (lose-switch). The both win-stay and lose-switch proportions were significantly higher in CC than in IC. The choice behaviors in CC and IC were best fitted by the Markov model that selects an action depending on the selected action and its outcome in the previous trial and a value-based reinforcement learning model, respectively.
The neuronal activities were consistent with the strategies the rats employed: (1) a feedback information (interaction between action and reward in the previous choice trial) was retained by about 10% of neurons in recorded regions until the next choice trial in CC, but reduced in IC (M1: 9% and 6%, DLS: 14% and 9%, PL: 5% and 4%, DMS: 13% and 8%, in CC and IC, respectively), and (2) information of action planed by win-stay lose-switch strategy was represented in CC but not in IC (M1: 15% and 0.4%, DLS: 9% and 0%, PL: 4% and 0.6%, DMS: 11% and 0.3%, in CC and IC, respectively).
These results demonstrated that choice strategies and their neuronal representations strongly depend on WM availability.
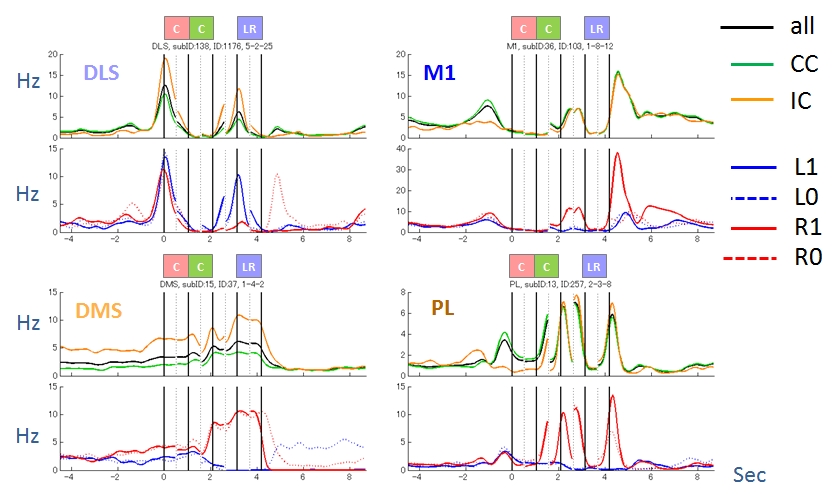
Figure 3.2.2: Activity patterns of four representative neurons. They were modulated by task condition (CC or IC), action (L or R) and reward (1 or 0).
3.2.3 The role of the cortico-basal ganglia loops for reward-motivated choice motor behavior [Tomohiko Yoshizawa, Makoto Ito]
The cortico-basal ganglia loops are known for their roles in both physical movement and reward-based decision making. To investigate the neural representation of the reward-motivated motor information in the loops, we recorded rat’s motion and the activities of 173 dorsomedial striatum (DMS), 71 dorsolateral striatum (DLS), 73 prelimbic cortex (PL) and 154 primary motor cortex (M1) neurons from 6 rats during a choice task.
The task was started by the presentation of choice tone (Tone C) or no-choice tone (Tone N) during the center hole poke. After Tone C, rats were required to select either the left or right hole by nose poke and then received a reward stochastically (choice trials). For Tone N, rats were not allowed to nose poke to left or right hole; otherwise Tone N was repeated (no-choice trials). The consecutive choice condition (CC) consisted of only choice trials. In the dispersed choice condition (DC), no-choice trials were inserted after every choice trial.
First, to examine which trial phase was related to the reward-motivated behavior, we analyzed rat’s head acceleration during 3 phases in CC (Cin: 200 ms until the center hole poke, Cout: 200 ms from moving out of the center hole, LRin: 200 ms until the left or right hole poke, Fig.1A). We found that the acceleration was significantly correlated with the mean reward of the past 6 trials only in Cout phase (Fig.1B). A regression analysis of neuronal activity revealed that the proportion of neurons coding the acceleration in Cout was significantly larger in DLS than in the other areas (DMS: 14%, DLS: 32%, PL: 16%, M1: 14%, Fig.1C).
Second, to exclude the possibility that DLS represented just particular motion (Cout) rather than reward-motivated behavior, we compared the behavior after Tone C and Tone N in DC. The acceleration of Cout after Tone C showed the correlation with the past reward, while the acceleration after Tone N did not. The proportion of neurons correlated with the acceleration in Cout after Tone C was significantly larger in DLS than in DMS (DMS: 8%, DLS: 18%, PL: 8%, M1: 13%). On the other hand, the proportion of neurons correlated with the acceleration in Cout after Tone N was significantly larger in M1 than in the others (DMS: 17%, DLS: 11%, PL: 14%, M1: 27%).
Our results suggest that the accelerated movement in Cout phase after Tone C was reward-motivated behavior, and that DLS processes the reward-motivated motor information while M1 is involved in general movements unaffected by reward.
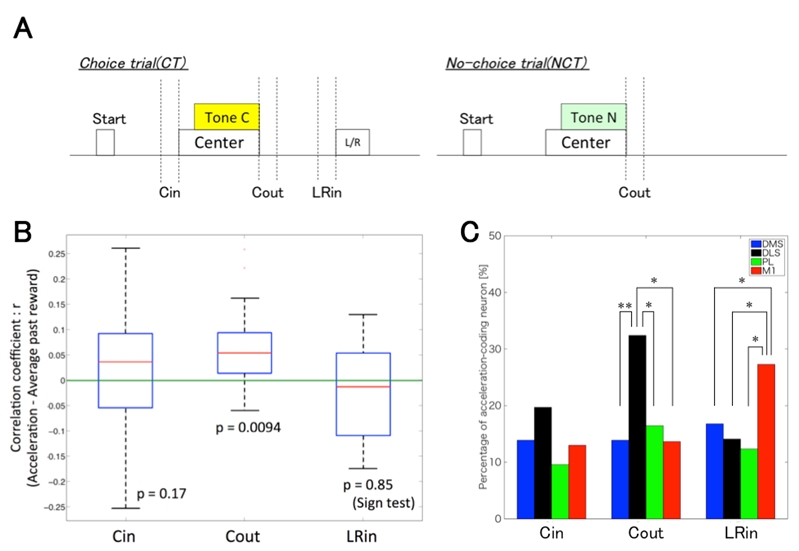
Figure 3.2.3: A, Schematic representation of trial phases. Cin: 200 ms until the center hole poke, Cout: 200 ms from moving out of the center hole, LRin: 200 ms until the left or right hole poke. B, Boxplot of correlation coefficient between each phase’s acceleration in CC and the average past reward. The acceleration in Cout phase was only correlated with the average past reward. The p-values were calculated by the sign test. C, The proportion of the acceleration-coding neurons in 3 phases in CC. The proportion of DLS neurons coding the acceleration in Cout was significantly larger than in the other areas. χ2 test, *: p < 0.05, **: p<0.01.
3.2.4 Investigation of action-dependent state prediction by two-photon microscopy [Akihiro Funamizu, collaboration with Professor Kuhn]
In uncertain and changing environments, we sometimes cannot get enough sensory inputs to know the current context, and therefore must infer the context with limited information to make a decision. We call such internal simulation of context a mental simulation. One illustrative example of the mental simulation happens in a game called watermelon cracking, in which a person tries to hit a watermelon far away with his eyes closed with a stick: the person needs to estimate his position based on his actions and sensory inputs, e.g., words from others. To investigate the neural substrate of mental simulation, we use two-photon fluorescence imaging in awake behaving mice which enables us to simultaneously image multiple identified neurons and their activities while the mouse conducts a task.
A mouse was head restrained and maneuvered a spherical treadmill. 12 speakers around the treadmill provided a virtual sound environment. The direction and the amplitude of sound pulses emulated the location of sound source, which was moved according to the mouse’s locomotion on the treadmill. When the mouse reached the sound source and licked a spout, it got a water reward. In some trials, the sound was intermittently omitted: the mouse asked to utilize a mental simulation to reach the sound source.
Calcium is an important second messenger in neurons and an increased calcium concentration is correlated with neuronal activity. For this reason we use a genetically encoded calcium indicator, called GCaMP6f, in posterior parietal cortex (PPC) of mice to detect neuronal activities. We could record the activities of more than 500 neurons simultaneously and of cortical layer 1 to 5 for one hour continuously (Figure). From the population activities in layer 2, we decoded the distance to sound source by a probabilistic decoder. The decoder could estimate the sound-source distance during no-sound periods, suggesting that PPC neurons represent and update the distance of sound source not only from present auditory inputs but also by dynamic update of the estimate using an action-dependent state transition model.

Figure 3.2.4: A. In-vivo imaging of neurons with two-photon microscopy. XZ plane reconstruction of calcium sensor expressing cortical neurons in posterior parietal cortex (i). The dotted line indicates the imaging plane of layer 2 in (ii). B. Distance estimation with a probabilistic decoder. Horizontal and vertical axes show the actual and estimated distance to sound source, respectively. The estimations were successful even during no-sound periods.
3.3 Adaptive Systems Group
3.3.1 Inverse reinforcement learning using inverse reinforcement learning
So far, we have developed the inverse reinforcement learning method based on the Linearly solvable Markov Decision Process in which the ratio between the controlled and uncontrolled state transition probabilities is estimated by the density ratio estimation. However, this method requires that the uncontrolled state transition probabilities should be constructed in advance. This study proposes a novel model-free inverse reinforcement learning method based on density ratio estimation under the framework of Dynamic Policy Programming. As opposed to our previous method, this method uses the ratio between the optimal and baseline stochastic policies and we show that the logarithm of the ratio between the optimal policy and the baseline policy is represented by the state-dependent cost and the value function.
In the same way as we did in our previous study, our proposal is to use density ratio estimation methods to estimate the density ratio of policies and the least squares method with regularization to estimate the state-dependent cost and the value function that satisfies the relation. As a result, our method can avoid computing the integral such as evaluating the partition function.

Figure 3.3.1: Vision based navigation task. (a): Image captured by the robot. (b): Environment where there exist three visual landmarks and five starting positions.
We conducted a real robot experiment as shown in Figure 3.3.1 to validate the proposed method, in which the task is to move from the start position to the destination. There exist three landmarks that has an LED with red, green, and blue LED light
emitting elements in the environment and the position of the green landmark is considered as the destination. Our robot called Spring Dog is a two-wheeled mobile robot and the pan-and-tilt camera head is mounted to get the environmental information.
Spring Dog obtains six image features and two joint angles of the camera head as state such as the center position and the number of blobs in the image plane. We prepared hand-coded features for reward while RBF features that are automatically expanded in the state space. The robot was controlled manually by the experimenter to collect the datasets in which the start position was selected from A, B, C and E in Figure 3.3.1 (b). On the other hand, we prepared a simple baseline controller that generated random behaviors to collect the baseline dataset.
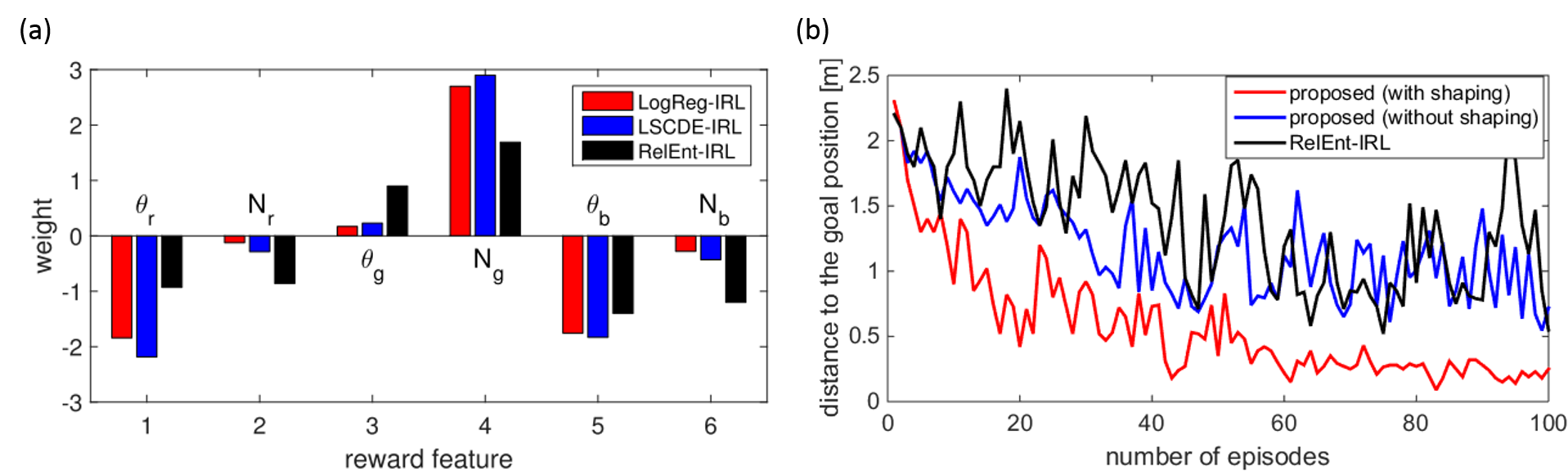
Figure 3.3.2: Experimental results of visual navigation task
According to the choice of the density ratio estimation algorithms, several implementations of our method were considered and we adopted LSCDE and LogReg. Our methods, LSCDE-IRL and LogReg-IRL were compared with RelEnt-IRL and the estimated weights are shown in Figure 3.3.2 (a). All the methods found a similar state-dependent reward that produced a positive value when the robot approached the red landmark. To evaluate the estimated state-dependent reward, we applied a forward reinforcement learning to learn a navigation behavior from the starting position D that was not included in the training data sets. Since one of the advantages of our method is to estimate the value function as well as the state-dependent reward function, the estimated value function can be used as a potential function of the shaping reward to accelerate the speed of learning. Figure 3.3.2 (b) compares the learning speed with and without shaping rewards, in which the performance was evaluated by the distance between the robot and the destination at the end of every episode. It is shown that the policy trained with the shaping reward converged faster
than that with the estimated reward. Note that the shaping reward is not computable in RelEnt-IRL because it does not estimate the value function.
3.3.2 Expected energy-based restricted Boltzmann machine for classification
In classification tasks, restricted Boltzmann machines (RBMs) have predominantly been used in the first stage, either as feature extractors or to provide initialization of neural networks. In this study, we propose a discriminative learning approach to provide a self-contained RBM method for classification, inspired by free-energy based function approximation (FE-RBM), originally proposed for reinforcement learning. For classification, the FE-RBM method computes the output for an input vector and a class vector by the negative free energy of a RBM. Learning is achieved by stochastic gradient-descent using a mean-squared error training objective. In an earlier study, we demonstrated that the performance and the robustness of FE-RBM function approximation could be improved by scaling the free energy by a constant that is related to the size of network. In this study, we propose that the learning performance of RBM function approximation can be further improved by computing the output by the negative expected energy (EE-RBM), instead of the negative free energy. To create a deep learning architecture, we stack several RBMs on top of each other. We also connect the class nodes to all hidden layers to try to improve the performance even further.
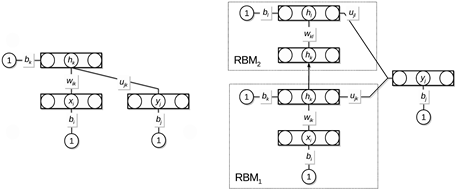
Figure 3.3.3: Architecture of the expected energy-based restricted Boltzmann machine.
We validate the classification performance of EE-RBM using the MNIST data set (see figure below) and the NORB data set, achieving competitive performance compared with other classifiers such as standard neural networks, deep belief networks, classification RBMs, and support vector machines. The purpose of using the NORB data set is to demonstrate that EE-RBM with binary input nodes can achieve high performance in the continuous input domain.
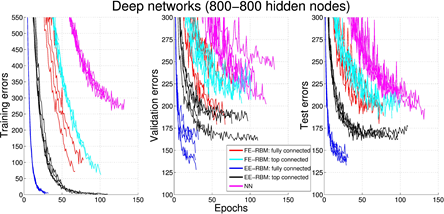
Figure 3.3.4: Experimental results of classification.
3.3.3 EM-based policy search reinforcement learning
A desk-top smartphone robot has proved to be an affordable, high-performance and low-cost robotic platform with its fast CPU, versatile built-in sensors, i.e. camera, gyro, accelerometer, GPS, open-source software developing environment and compatible actuators, i.e. Arduino, Raspberry Pi and IOIO. With the overall goal to construct a multi-agent system for researching robot social behaviors which expands its replicable potential, we started with developing a two-wheel balancer. So far, we have developed control architectures of our robots to realize balancing behaviors, but all the control parameters have been tuned by hand.
To optimize the control parameters automatically and transfer the learned policy to the real smart smartphone robot, we propose a novel policy search algorithm called EM-based Policy Hyper Parameter Exploration for a smartphone robot to learn its policy parameters. This method integrates two reinforcement learning algorithms: Policy Gradient with Parameter Exploration (PGPE) and EM-based Reward-Weighted Regression. Like PGPE, our method can utilize a deterministic policy and the policy parameters are sampled at the beginning of each episode. This procedure reduces the variance of the actual return. In addition, the update rule does not require a learning rate because it is derived based on the reward-weighted regression using the EM algorithm.
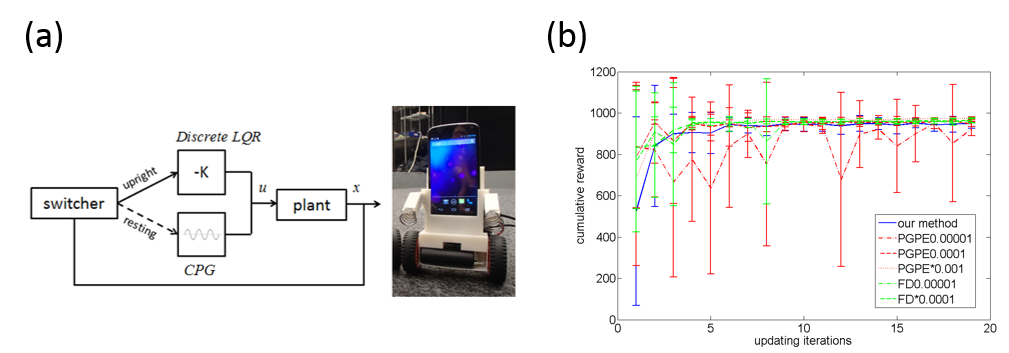
Figure 3.3.5: (a) Switching control architecture and our Android-based smartphone robot. (b) Comparision of learning curves.
The proposed method is tested in using a two-wheeled smartphone robot. Figure 3.3.5 (a) shows the switching control framework with a discrete-time Linear Quadratic Regulator (LQR) for stabilizing to balance and a Central Patter Generator (CPG) for destabilizing to stand up. The feedback gain K and the paramters of the CPG are optimized by our method. Figure 3.3.5 (b) compares the learning curve between our method and previous methods such as PGPE and FD, where we pick up some appropriate learning rates for the previous methods. Experimental results show that our method is able to achieve the similar performance as the other two when the learning rates are tuned carefully. And the desired behaviors have been successfully achieved.
4. Publications
4.1 Journals
- Elfwing, S. & Doya, K. Emergence of Polymorphic Mating Strategies in Robot Colonies. Plos One, doi:10.1371/journal.pone.0093622 (2014).
- Elfwing, S. U., Eiji, Doya, Kenji. Expected energy-based restricted Boltzmann machine for classification. Neural Networks Online 28 September, doi:10.1016/j.neunet.2014.09.006 (2014).
- Funamizu, A., Ito, M., Doya, K., Kanzaki, R. & Takahashi, H. Condition interference in rats performing a choice task with switched variable- and fixed-reward conditions. Front Neurosci 9, doi:doi: 10.3389/fnins.2015.00027. eCollection 2015. (2015).
- Ito, M. & Doya, K. Distinct Neural Representation in the Dorsolateral, Dorsomedial, and Ventral Parts of the Striatum during Fixed- and Free-Choice Tasks. Journal of Neuroscience 35, 3499-3514, doi: doi: 10.1523/JNEUROSCI.1962-14.2015. (2015).
- Kunkel, S., Schmidt, M., Eppler, M. J., Plesser, H. E., Masumoto, G., Igarash, J., Ishii, S., Fukai, T., Morrison, A., Diesmann, M. & Moritz, H. Spiking network simulation code for petascale computers. Frontiers in Neuroinfomatics 8 (2014).
- Miyzaki, W. K., Miyazaki, K., Tanaka, F. K., Yamanaka, A., Takahashi, A., Tabuchi, S. & Doya, K. Optogenetic Activation of Dorsal Raphe Serotonin Neurons Enhances Patience for Future Rewards. Current Biology, doi:http://dx.doi.org/10.1016/j.cub.2014.07.041 (2014).
- Nakano, T., Otsuka, M., Yoshimoto, J. & Doya, K. A Spiking Neural Network Model of Model-Free Reinforcement Learning with High-Dimensional Sensory Input and Perceptual Ambiguity. Plos One, doi:10.1371/journal.pone.0115620 (2015).
- Doya, K. in Japanese Journal of Molecular Psychiatry Vol. 15 分子精神医学 1(1) (2015).
- Funamizu, A. & Doya, K. in Seitaino Kagaku Vol. 66 生体の科学 33-37 (2015).
- Miyazaki, K. W., Miyazaki, K. & Doya, K. in Seitaino Kagaku Vol. 66 生体の科学 38-43 (2015).
- Okada, G. O., Yasumasa, Shishida, K. U., Kazutaka, Onoda, K., Kunisato, Y., Tanaka, C. S. D., Kenji & Yamawaki, S. in Seishin Shinkeigaku Zasshi Vol. 116 精神神経学会雑誌 825-831 (2014).
4.2 Books and other one-time publications
- Nothing to report
4.3 Oral and Poster Presentations
- Doya, K. Toward the neurophysiology of mental simulation, in 17th World Congress of Psychophysiology (IOP2014), International Conference Center Hiroshima (2014).
- Doya, K. Control of Patience and Serotonin, in SHANGHAI COLLOQUIM in NEUROECONOMICS, NYU Shanghai Pudong Campus, CHINA (2015).
- Elfwing, S. Robocopulation: A robot evolution approach to study polymorphic mating strategies, in Maker Faire Rome 2014, Parco Della Musica Auditorium Rome, Italy (2014).
- Doya, K. Machine learning and brain science, in FAN2014 in Kitami, Kitami Institute of Technology(Kitami-shi, Hokkaido) (2014).
- Doya, K. Robotics: Machine learning and brain science, in Okinawa General Bureau, 4th Kumikomi Sangyo Forum - Seminar, Naha city, Okinawa (2015).
- Igarashi, J. A large-scale simulation of neural networks and development of a realistic model of motor cortex performed on K computer: Toward reproduction of Parkinson's disease symptoms, in Neurocomputing meeting, OIST, Okinawa, Japan (2014).
- Doya, K. Machine learning and brain science, in 14th International conference on Intelligent Systems Design and Applications (ISDA2014), OIST Seaside House (2014).
- Doya, K. How to cope with delayed rewards, in The team meeting: MEXT Sponsored research Brain Project G, OIST(Onna-son, Okinawa) (2014).
- Doya, K. Introduction to numerical methods for ordinary and partial differential equations, in Okinawa Computational Neuroscience Course 2014, OIST Seaside House (2014).
- Doya, K. Introduction to reinforcement learning and Bayesian inference, in Okinawa Computational Neuroscience Course 2014, OIST Seaside House (2014).
- Igarashi, J. Perspective on Japanese projects of large-scale neural network simulation in the next in 1st community workshop HBP network simulator “Are we building the right thing? – Requirements from theory for simulation environments and neuromorphic computing”, European Institute for Theoretical Neuroscience(EITN), Paris, France (2015).
- Igarashi, J., Helias, M., Kunkel, S., Masumoto, G., Fukai, T., Ishii, S., Diesmann, M., Moren, J., Shouno, O., Yoshimoto, J. & Doya, K. Simulation of neural networks on K computer toward production of Parkinson's disease symptoms and whole brain simulation on next generation super computer in 2014 Smoky Mountains Computational Sciences and Engineering Conference and U.S./Japan Exascale Applications Workshop, Tennessee, US (2014).
- Sezener, C. E., Uchibe, E. & Doya, K. Obtaining reward functions of rats using inverse reinforcement learning, in Turkish Autonomous Robots Conference, Ankara, Turkey (2014).
- Tokuda, T., Yoshimoto, J., Shimizu, Y., Toki, S., Okada, G., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K. A novel approach to defining functional connectivity of fMRI data, in 24th Annual Conference o Japan Neural Network Society(JNNS2014), Hakodate Future University (Hakodate, Hokkaido) (2014).
- Tokuda, T., Yoshimoto, J., Shimizu, Y., Yoshida, K., Toki, S., Okada, G., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S., Yahata, N. & Doya, K. Bayesian multiple and co-clustering methods: Application to fMRI data, in IPSJ (Information ProcessingSociety of Japan) SIG conference, OIST Okinawa (2014).
- Uchibe, E. & Doya, K. Combining learned controllers to achieve new goals based on linearly solvable MDPs, in IEEE International Conference on Robotics and Automation, HongKong (2014).
- Wang, J., Uchibe, E. & Doya, K. Control of Two-Wheel Balancing and Standing-up Behaviors by an Android Phone Robot, in The 32nd Annual Conference of the Robotics Society of Japan, Kyushu Sangyo University, Fukuoka, Japan (2014).
- Yoshimoto, J., Kannon, T., Amano, M., Nishioka, T., Usui, S. & Kaibuchi, K. Neural PhosphoSignaling Database: A New Omics Database Supporting Neuroscience Research, in INCF Japan Node International Workshop: Advances in Neuroinformatics 2014 (AINI 2014), RIKEN (Wako) (2014).
- Doya, K. The brain’s mechanisms for reinforcement learning: The roles of dopamine, serotonin, and the basal ganglia, in The 19th workshop on affective and social behaviors and psychiatry, Kyoto University (2014).
- Doya, K. Reinforcement learning in robots and the brain, in 160th SIG Human-Computer Interaction, IPSJ, OIST Seaside House (Onna, Okinawa) (2014).
- Doya, K. The duality of estimation and control and the architecture of the brain, in Joint Conference on Autonomous Control, Ikaho, Gunma (2014).
- Doya, K. Computational theory and neural mechanism of reinforcement learning, in Society for young researcher on Neurosceicne: Spring Retreat 2015 Hotel Wing International Sagamihara, Kanagawa (2015).
- Funamizu, A., Kuhn, B. & Doya, K. Investigation of neural inplementation of model-based decision making with two-photon microscopy, in National Insititute for Physiological Sceience(NIPS)research meeting: Investigation of neural mechanism from glial cells, National Insititute for Physiological Sceience(NIPS) (2014).
- Hamada, H. MRI in OIST, in MRI research meeting, (2015).
- Igarashi, J. Selection of movements by lateral inhibition in a realistic model of motor cortex, in The 6th acceleration technical release debate, OIST, Okinawa, Japan (2014).
- Miyazaki, K. Serotonin and patience, in 92nd Annual meeting of the Physiological society of Japan, Kobe International Conference Center (Kobe) (2015).
- Uchibe, E. D., Kenji. Inverse Reinforcement Learning Using Density Ratio Estimation, in The 32nd Annual Conference of the Robotics Society of Japan, Kyushu Sangyo University, Fukuoka, Japan (2014).
- Funamizu, A., Kuhn, B. & Doya, K. Action-dependent state prediction in the parietal cortex of mouse during a virtual navigation task, in Neuroscience 2014, Society for Neuroscience, Washington, DC (2014).
- Funamizu, A., Kuhn, B. & Doya, K. Imaging action-dependent state prediction in mouse posterior parietal cortex, in Comprehensive Brain Science Network Winter Symposium 2014, Bunkyo-ku, Tokyo (2014).
- Funamizu, A., Kuhn, B. & Doya, K. Imaging action-dependent state prediction in mouse parietal cortex, in FENS-Hertie Winter School “The neuroscience of decision making”, Obergurgl, Austria (2015).
- Igarashi, J., Moren, J., Yoshimoto, J. & Doya, K. Selective activation of columnar neural population by lateral inhibition in a realistic model of primary motor cortex, in Neuroscience 2014(SfN) Washington, D.C USA (2014).
- Miyazaki, K., Miyazaki, K. W., Tanaka, K., Yamanaka, A., Takahashi, A. & Doya, K. Promotion of patience by dorsal raphe serotonin neuron activation depends on the certainty of future rewards, in Neuroscience 2014 (SfN), Washington, D.C. USA (2014).
- Moren, J., Igarash, J., Shouno, O., Sreenivasa, M., Doya, K., Ayusawa, K. & Nakamura, Y. On-line integration of multiple neural network and musculoskeletal models, in Neuroinformatics 2014 7th INCF Congress, Leiden, The Netherlands (2014).
- Moren, J., Igarashi, J., Yoshimoto, J. & Doya, K. Large-scale integrated models of basal ganglia-thalamo-cortical circuit toward reproducing Parkinson's symptoms in 5th AICS International Symposium Computer and Computational Sciences for Exascale Computing, RIKEN AICS (Kobe, Hyogo) (2014).
- Reinke, C., Uchibe, E. & Doya, K. A critical view on the Model based/Model free learning theory, in The 7th Research Area Meeting Grant-in Aid for Scientific Research on Innovative Areas: Elucidation of the Neural Computation for Predition and Decision Making, OIST (2014).
- Reinke, C., Uchibe, E. & Doya, K. Gamma-QCL: Learning multiple goals with a gamma-submodular model-free reinforcement learning framework, in 15th Winter Workshop on Mechanism of Brain and Mind, Rusutsu, Hokkaido (2015).
- Shimizu, Y., Yoshimoto, J., Toki, S., Okada, G., Takamura, M., Okamoto, Y., Yamawaki, S. & Doya, K. Analysis of Depression and Treatment Response based on Behavioural Data and Biomarkers -Preliminiary results in 24th Annual meeting of Japanese Neural Network Society (JNNS2014), Hakodate Future University (Hakodate, Hokkaido) (2014).
- Shouno, O. & Doya, K. Local circuit model of the subthalamo-pallidal network for the generation of parkinsonian oscillations, in 23rd Annual meeting of Computational Neuroscience Meeting (CNS2014),, Quebec city, Canada (2014).
- Tokuda, T. Y., Junichiro, Shimizu, Y., Toki, S., Okada, G., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K. A novel approach to defining functional connectivity of fMRI data, in 24th Annual Conference o Japan Neural Network Society(JNNS2014), Hakodate Future University (Hakodate, Hokkaido) (2014).
- Yoshida, K. Y., Junichiro, Shimizu, Y., Toki, S., Takamura, M., Okamoto, Y., Yamawaki, S. & Doya, K. Diagnosis of Depression with Spicy MKL, in 24th Annual meeting of Japanese Neural Network Society (JNNS2014), Hakodate Future University (Hakodate, Hokkaido) (2014).
- Yoshizawa, T. I., Makoto & Doya, K. Neural representation of task-level and motor information in the cortico-basal ganglia loops, in Neuroscience 2014, Pacifico Yokohama (2014).
- Yukinawa, N., Doya, K. & Yoshimoto, J. A Kinetic Signal Transduction Model for Structural Plasticity of Striatal Medium Spiny Neurons, in 3rd Annual Winter q-bio Meeting, Maui, Hawaii, USA (2015).
- Funamizu, A. Presentation Investigation of action-dependent state prediction in the mouse parietal cortex with two-photon microscopy in Neuroscience2014, Pacifico Yokohama (2014).
- Igarashi, J., Moren, J., Yoshimoto, J. & Doya, K. Presentation Selection of outputs by horizontal connection in a realistic model of primary motor cortex, in Neuroscience2014, Pacifico Yokohama (2014).
- Ito, M. Presentation Dissociation of working memory-based and value-based strategies in a free-choice task, in Neuroscience 2014, Pacifico Yokohama (2014).
- Yukinawa, N. Presentation Multiphysics simulation of striatal medium spiny neurons, in BSCRC Winter School 2015, Aichi, Japan (2015).
5. Intellectual Property Rights and Other Specific Achievements
None.
6. Meetings and Events
6.1 Sponsored Research Meeting: The team meeting of Field G in MEXT Strategic Research Program for Brain Sciences
- Date: April 14-16, 2014
- Venue: OIST Campus, Seminar Room B250 & Seminar Room C210
- Organizer: Field G in MEXT Strategic Research Program for Brain Sciences
- Speakers :
- Jeff Wickens, Okinawa Institute of Science and Technology
- Kenji Doya, Okinawa Institute of Science and Technology
6.2 Joint workshop: Neuro-computing, bioinformatics, mathematical modeling and machine learning
- Date: June 25-27, 2014
- Venue: OIST Capmpus, Semiar Room B250 & Seminar Room C210
- Co-organizers:
- The Institute of ElectronicsInformation and Communication Engineers(IEICE)
- Information Processing Society of Japan
- IEEE Computational Intelligence Society Japan Chapter
- Japan Neural Network Society
- Speaker: Jun Igarashi, Okinawa Institute of Science and Technology
6.3 Sponsored Research Meeting: The 7th Research Area Meeting of the Elucidation of the Neural Computation for Prediction and Decision Making
- Date: June 6-8, 2014
- Venue: Media Center, Kitakyushu Science and Research Park, Kyushu Institute of Technology
- Organizer: Grant-in Aid for Scientific Research on Innovative Areas, MEXT, JAPAN, Elucidation of the Neural Computation for Prediction and Decision Making
- Speakers:
- Kenji Matsumoto, Tamagawa Univesity Brain Science Institute
- Masahiko Haruno, CiNet: Center for Information and Neural Networks
- Tomohiro Shibata, Prof. Kyusyu Institute of Technology
6.4 Joint Symposium: Prediction and Decision Making & The Science of Mental Time
- Date: December 13, 2014
- Venue: Tokyo Medical and Dental University
- Co-organizers : Grant-in Aid for Scientific Research on Innovative Areas, MEXT, JAPAN, Elucidation of the Neural Computation for Prediction and Decision Making & The Science of Mental Time, Investigation into the past, present and future
- Speakers:
- Shigeru Kitazawa, Osaka University
- Kenji Doya, Okinawa Institute of Science and Technology
- Maki Tanaka, Hokkaido University
- Katsuhiko Miyazaki, Okinawa Institute of Science and Technology
- Yuji Ikegaya, The University of Tokyo
- Hiroyuki Nakahara, RIKEN BSI
6.5 Sponsored Research Meeting: The 8th Research Area Meeting of the Elucidation of the Neural Computation for Prediction and Decision Making
- Date: December 11, 2014
- Venue: Tokyo Medical and Dental University
- Co-organizers : Grant-in Aid for Scientific Research on Innovative Areas, MEXT, JAPAN, Elucidation of the Neural Computation for Prediction and Decision Making
- Speakers:
- Mitsuhiro Okada, Keio Unibersity
- Tomohiro Shibata, Kyusyu Institute of Technology
- Keiichi Kitajo, RIKEN BSI
- Jun Morimoto, ATR
- Masamichi Sakagami, Tamagawa University
- Kenji Doya, Okinawa Institute of Science and Technology
- Hitoshi Okamoto, RIKEN BSI
- Hidehiko Takahashi, Kyoto University
- Minoru Kimura, Tamagawa Univeristy
- Takatoshi Hikida, Kyoto University
6.6 Seminar
Title: A neuro-computational account of emotional conflict adaptation
- Date: April 7, 2014
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Naho Ichikawa, Research Associate, Stanford University School of Medicine Department of Psychiatry.
Title: Acquisition via Human Sensorimotor Learning
- Date: August 13
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Erhan Oztop, associate professor at Ozyegin University, Istanbul, visiting researcher at ATR.
Title: Active mechanisms of learning and decision making
- Date: August 25, 2014
- Venue: OIST Campus Center Building, Seminar Room C209
- Speaker: Rei Akaishi, Frontal Lobe Project, Tokyo Metropolitan Institute of Medical Science
Title: Application of computational model of decision-making to psychiatric disorders
- Date: October 31, 2014
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Saori C Tanaka, ATR Brain Information Communication Research Lab. Group
Title: Machine learning for wearable robotics
- Date: November 7, 2014
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Patrick van der Smagt, Professor, Computer science at TUM
Title: Computational Biology, Machine Learning, Biological Databases & Knowledge Extraction, A Few Examples
- Date: November 14, 2014
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Jovan David Rebolledo Méndez, Tactile Analogics LLC
Title: Explaining inter-individual differences at behavioural and neurophysiological levels - Factored representations in dual-learning systems
- Date: November 27, 2014
- Venue: OIST Campus Lab1. Seminar Room D014
- Speaker: Florian LESAINT, PhD @ ISIR (UPMC)
Title: The First Neural Connectomics Challenge: Results and Research Opportunities
- Date: November 25, 2014
- Venue: OIST Campus Lab1. Seminar Room D015
- Speaker: Ildefons Magrans de Abril, Postdoctoral Fellow, Vrije Universiteit Brussel
Title: Decorrelation in spiking network models
- Date: December 2, 2014
- Venue: OIST Campus Center Building. Seminar Room B503
- Speaker: JESUS MANRIQUE GOMEZ
Title: Beyond Thermodynamics: the Physics of Matter, Life, and Awareness
- Date: December 16, 2014
- Venue: OIST Campus Center Building. Seminar Room C210
- Speaker: Piet Hut, Professor of Interdisciplinary Studies Institute for Advanced Study
Title: Intelligence and Embodiment: A Statistical Mechanics Approach
- Date: January 15, 2015
- Venue: OIST Campus Lab1. Meeting Room C016
- Speaker: Alejandro Chinea Manrique de Lara Department of Physics of the Faculty of Sciences of the UNED, (Madrid)
Title: Unsupervised Classification for Main Features Extraction in Natural Disaster Text Sources
- Date: January 26, 2015
- Venue: OIST Campus Lab1. Meeting Room D015
- Speaker: Carlos Gutierrez, University of the Ryukyus



