Neural Computation Unit

Professor Kenji Doya

Abstract

The Neural Computation Unit pursues the dual goals of developing robust and flexible learning algorithms and elucidating the brain’s mechanisms for robust and flexible learning. Our specific focus is on how the brain realizes reinforcement learning, in which an agent, biological or artificial, learns novel behaviors in uncertain environments by exploration and reward feedback. We combine top-down, computational approaches and bottom-up, neurobiological approaches to achieve these goals. The major achievements of the three subgroups in the fiscal year 2013 are the following.

a) The Dynamical Systems Group  developed a large-scale spiking neuron model of the basal ganglia-thalamo-cortical loops to understand the symptoms of Parkinson's disease. The group also applied machine learning methods for subtype identification and diagnosis of depression patients using functional MRI and other neurobiological data. In collaboration with Prof. Kaibuchi's lab in Nagoya U, the gourp created a database of  phosphoproteomics comprehensive understanding dopamine-related signaling pathways and also a new signaling cascade models including dopamine D2 receptors and adenosine recepters.

b) The Systems Neurobiology Group revealed that optogenetic activation of serotonin neurons facilitates waiting for delayed rewards and that the effect is not simply by motor inhibition. Through neural recording and analysis of the striatum and the cortex of rats, the group revealed that these there are nourons involved in different strategies of choice behaviors and at different abstraction levels of the behavioral. In collaboration with Prof. Kuhn, the group performed two-photon imaging of mice's parietal cortical neurons and analyzed the neural substrates of mental simulation.

c) The Adaptive Systems Group developed an efficient inverse reinforcement learning algorithm using the framework of linearly solvable Markov decision process (LMDP). Using the embodied evolution framework of Cyber Rodent robots, the group revealed that polymorphic mating behaviors can emerge and be stable in a robot colony. The group is also developing a robot platform using smartphones and realized dynamic stading up and balancing behaviors.

1. Staff

• Dynamical Systems Group
  • Dr. Junichiro Yoshimoto, Group Leader
  • Dr. Jun Igarashi, Researcher
  • Dr. Jan Moren, Researcher
  • Dr. Makoto Otsuka, Researcher
  • Dr. Osamu Shouno, Researcher
  • Dr. Tomoki Tokuda, Researcher
  • Dr. Naoto Yukinawa, Researcher
  • Kosuke Yoshida, Special Research Student
• Systems Neurobiology Group
  • Dr. Makoto Ito, Group Leader
  • Dr. Akihiro Funamizu, JSPS Research Fellow
  • Dr. Katsuhiko Miyazaki, Researcehr
  • Dr. Kayoko Miyazaki, Researcher
  • Dr. Yu Shimizu, Researcher
  • Ryo Shiroishi, Special Research Student
  • Tomohiko Yoshizawa, Special Research Student
• Adaptive Systems Group 
  • Dr. Eiji Uchibe, Group Leader
  • Dr. Stefan Elfwing, Researcher
  • Ken Kinjo, Special Research Student
  • Naoto Yoshida, Special Research Student
  • Jiexin Wang,Special Research Student
• Administrative Assistant / Secretary
  • Emiko Asato
  • Kikuko Matsuo

2. Collaborations

• Theme: The research of biologically-inspired reinforcement learning systems for human-centered interface intelligence of future machines
  • Type of collaboration: Joint research
  • Researchers:
    •  Masato Hoshino, Honda Research Institute Japan Co., Ltd
    • Osamu Shouno, Honda Research Institute Japan Co., Ltd
    • Hiroshi Tsujino, Honda Research Institute Japan Co., Ltd

3. Activities and Findings

3.1 Dynamical Systems Group

3.1.1 Large-scale spiking neuron models of the basal ganglia-thalamo-cortical loops [Moren, Igarashi, Shouno, Yoshimoto]

The basal ganglia are the locus of Parkinson's disease through the loss of dopamine-neurons in the substantia nigra pars compacta, and the basal ganglia-thalamo-cortical loops are known to play a critical role in the development of tremor and other motor-related symptoms. However, the precise mechanisms by which the loss of dopaminergic neurons gives rise to parkinsonian tremor are still unknown. Aiming at understanding the parkinsonian pathology as a dynamical system, we attemp to construct an integrated set of realistic models of the basal ganglia-thalamo-cortical areas.

In the basal ganglia, abnormal oscillatory burst activities whose frequencies ranges 8-30 Hz are often observed in neurons of the subthalamic nucleus (STN) and globus pallidus external/internal (GPe/GPi) of patients and nonhuman-primates model of the Parkinson’s disease, and implicated in symptoms of Parkinson’s disease, such as akinesia, bradykinesia and rigidity. To reveal these mechanisms, we have constructed spiking neural network models of STN-GPe circuitry. We found that post-inhibitory rebound potentiation of STN neurons and short-term synaptic plasticities are required for the pathological oscillatory burst activities (Figure 3.1.1). This suggests that strengthened connectivity between STN and GPe and reduced autonomous activity of GPe neurons, both of which are known to be caused by dopamine depletion, switch neuronal discharges in STN and GPe from normal to the parkinsonian states.

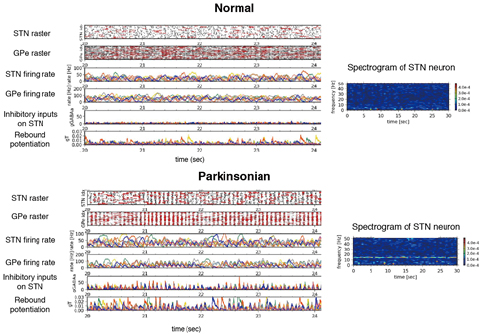
Figure 3.1.1: Typical activity of a STN-GPe circuit (64 and 192 neurons for respective nuclei) and spectrogram of a STN neuron in the circuits. Upper two panels correspond “Normal” state and lower two panels correspond “Parkinsonian” state. In rater plots, only activities of randomly-selected 20 neurons are represented. Red vertical bars in raster plots indicate spikes in bursts. In other traces, only 8 neurons are represented with identical colors. Inhibitory inputs on a STN neuron indirectly show an effect of short-term depression at a GPe-to-STN GABA-A synapse. gT represents a strength of post-inhibitory rebound potentiation of a STN neuron.

In the motor cortex and thalamus of Parkinson's disease patients with tremor symptom, alpha oscillation (8-12Hz) occurs with coupled with electromyograph (EMG) signals of antagonistic muscles in peripherals. The EMG signals of the extensor and the flexor are mutually coupled at reverse phase, and the frequency range are about half of alpha oscillation. With the abnormal oscillation from basal ganglia, how motor cortex and thalamus are involved with the generation of tremor has not been made clear. To investigate this, we have been developing a spiking neural network model of motor cortex and thalamus according to electrophysiological and anatomical data. We have confirmed reproduction of some basic neural behaviour observed in experiments, for instance, theta-alpha oscillation (4-12Hz) in thalamus, and lateral inhibition among the cortical columns in the motor cortex (Figure 3.1.2).

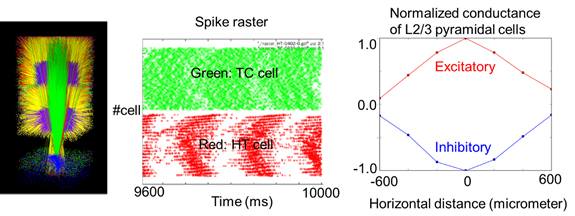
Figure 3.1.2: Network structure and neural activities of corticothalamic model. Left: 3D image of corticothalamic model. Middle: oscillatory neural activity in alpha frequency range of a model of thalamus. Right: Stimulus position and normalized amplitude of excitatory and inhibitory conductances of layer 2/3 pyramidal cell in motor cortex model.

3.1.2 Automatic diagnosis and subtype discovery of depressive disorder based on fMRI recordings and machine learning [Shimizu, Tokuda, Yoshida, Yoshimoto]

Diagnosis of depression is currently based on long interviews. In the search for an objective and more efficient method to diagnose this complex disease we analyze multidimensional data, including structural magnetic resonance imaging (MRI) data, functional MRI data involving four different tasks, resting state data, as well as genetic polymorphism and behavioral tests, obtained from (currently 130) depression patients and (currently 120) healthy controls using machine learning algorithms. We investigate how subtypes can be identified and how they can be categorized so as to provide a basis for adequate treatment methods.

As the first step to our goal, we subjected each data set separately, but also combinations of different datasets, to three types of logistic classifiers with LASSO (least absolute shrinkage and selection operator) regularizers, namely standard LASSO (sLASSO), group LASSO (gLASSO) and sparse group LASSO (sgLASSO). The best classification performance was achieved with group LASSO and a combination of fMRI data from a semantic and a phonological semantic task. Depressed subjects could be distinguished from controls with an accuracy of 91.95±2.02% (sensitivity: 91.35±2.90%, specificity: 92.55±2.70%, Figure 3.1.3(a)). As summarized in Figure 3.1.3(b), the analysis reveals two interesting findings: 1) Depressed subjects, who were wrongly classified as controls (false negative) and control subjects, who were wrongly classified as depressed (false positive) had low absolute discriminative score (<0.2); and 2) all false negative patients showed good improvement of their symptoms 6 weeks later (Hamilton depression scale < 11, remission).

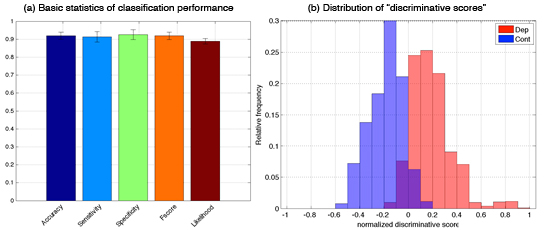
Figure 3.1.3: Best classification results for imaging data: semantic combined with phonological verbal fluency data (a) Basic statistics of classification performance. (b) Distribution of “discriminative scores” for the test data (i.e. the data unused in the training phase). Positive and negative discriminative scores mean that the corresponding data are classified into the depressive and control groups, respectively; and their absolute values indicates the degree of the confidence.

Based on the best classifier, we estimated the locations in the brain contributing to the identification of depressed subjects (red in Figure 3.1.4) and the healthy subjects, respectively (blue in Figure 3.1.4). Main contributing brain areas were: left precuneus, left precentral gyrus, left inferior frontal cortex (pars triangularis), left cerebellum (crus1) (semantic data), left inferior frontal operculum, left post central gyrus, left insula, left middle frontal cortex, left middle temporal cortex, right precuneus, right middle temporal cortex, left inferior frontal cortex, left precentral gyrus and left precuneus (phonological data).

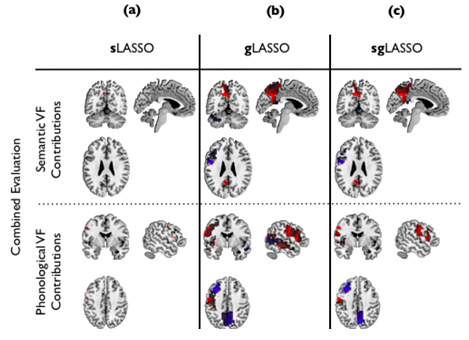
Figure 3.1.4:  Brain areas contributing to the classification of combined semantic and phonological fMRI data. Red and blue indicate locations in the brain contributing to the identification of depressed subjects and healthy subjects, respectively. The columns correspond to three different classifiers: (a) sLASSO; (b) gLASSO; (c) and sgLASSO, respectively.

For the purpose of identifying subtypes of depressive subjects, we developed a Gaussian co-clustering method that enables to simultaneously cluster both rows (subject) and columns (feature) in a given data matrix. In our context of analyzing functional Magnetic Resonance Imaging (fMRI) data (subject × feature), this Bayesian method of clustering has an advantage that it can reveal possible feature-clusters that may be differently relevant to the subject-clusters. Further, since in our method the number of clusters both for rows and columns can be inferred from the data by means of Dirichlet process, it is computationally efficient.

We applied this method to resting state fMRI data. First, we pre-processed the data as follows. We divided the whole brain into 140 sub-regions based on anatomical divisions (sulci), and calculated correlations of mean time-course activations between pairs of sub-regions. Further, the data of depressive subjects were vectorized and subsequently standardized using means and standard deviations for control subjects. As a result, we obtained functional connectivity MRI data (fcMRI) with the size of 59 (depressive subjects) × 9730 (connects).

Next, we applied the Gaussian co-clustering method to this dataset, which resulted in 15 connect-clusters and 7 subject-clusters. The outcome of the co-clustering is summarized in Figure 3.1.5 in which the mean functional connectivity in connect-clusters and the mean remission rate of depression in each subject-cluster are compared. Note that the remission is evaluated based on Hamilton Rating Scale for Depression (HRSD) score after 6 weeks of the onset of Selective Serotonin Reuptake Inhibitors (SSRI) treatment, while the fMRI data were collected before the onset of the treatment. It is suggested in Figure 3.1.5 that the level of functional connectivity in a subject-cluster is related to the level of remission. To clarity this, we further evaluated correlations between the mean functional connectivity and the HRSD score over subjects (Figure 3.1.6). It was found that the correlations between functional connectivity in connect-clusters 13, 14 and 15, and the HRSD score are significant (α=0.05). Furthermore, the following brain regions were identified as relevant to the connect-clusters 13, 14 and 15, based on the number of edges: Paracentral lob, Hippocampus, Postcentral lob, Temporal_Mid, Temporal_inf, and Frontal_Med_Orb. These results imply a possibility that the derived subject-clusters (hence, subtypes of depressive subjects) may be characterized by the treatment effect of SSRI with the aforementioned brain regions as relevant brain areas.

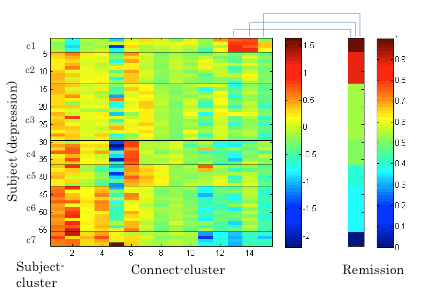
Figure 3.1.5: Mean functional connectivity in connect-clusters and remission rate of depression for subject-clusters.

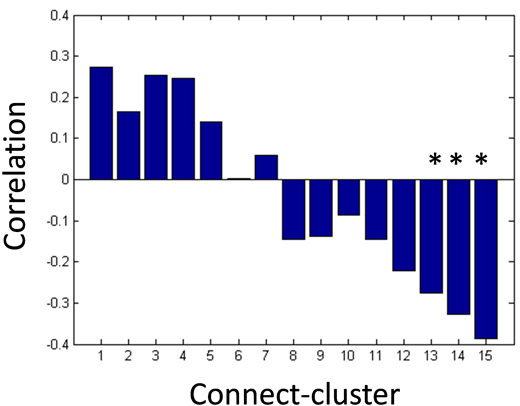
Figure 3.1.6: Peasron correlation coefficients between mean functional connectivity and HRSD score after 6 weeks of SSRI treatment (*p-value < 0.05).

3.1.3 Multiscale modeling of striatal medium spiny neurons [Yukinawa, Yoshimoto]

The dopamine-dependent plasticity of cortico-striatal synapses is supposed to play a critical role in reinforcement learning. In our former model-study, it was predicted that the dopaminergic inputs and the calcium responses affect the synaptic plasticity of "direct" medium-spiny neurons (MSNs), which express D1-type dopamine receptors (D1Rs) and innervate the direct pathway in the basal ganglia circuit, by way of the signaling cascades within the synaptic spines. However, about half population in the striatum consists of “indirect” MSNs, which express D2-type dopamine receptors (D2Rs) and innerviates the indirect pathway in the basal ganglia circuit, and direct and indirect MSNs have complementary neurophysiological properties. To elucidate the biophysical mechanism and functions of the complementary properties, we started with the construction of a kinetic model for intracellular signal transduction of indirect MSNs. The model is based on the following biochemical findings: 1) D2Rs show higher affinity to dopamine than D1Rs; 2) D1Rs and D2Rs are coupled with different types of G proteins - D1Rs are coupled with Gs/olf which activates adenylyl cyclase AC5 while D2Rs are coupled with Gi which inactivates AC5; and 3) D2Rs have an antagonistic interaction with A2A-type adenosine receptors (A2ARs) that is expressed selectively in indirect MSNs while D1Rs does not have the interaction.

Using this model, we predicted the response of cAMP, as a second messanger of dopamine and adenosine inputs. As a result, the direct and indirect MSNs exhibit flip-flop-like response to the dopamine input under physiological conditions, but the upregulation of indirect MSNs by low dopamine input diminished in the absence of adenosine. To confirm the contribution of the cAMP response to the synaptic plasticity, the model was further integrated with the downstream signaling pathways of cAMP based on the previous works, and then we simulated dopamine-dose dependent phosphoresponses of the AMPA receptor subunit GluR1, responsible for the cortico-striatal synaptic efficacy. The results suggest that the phosphoresponses in the D1R MSNs and D2R MSNs are observed only when dopamine level increases or decreases, respectively. Interestingly, it was predicted that the steady level of adenosine is crucial for the phosphoresponce in the D2R MSNs (Figure 3.1.7). Finally, we integrated the intracellular model with a conductance-based point model of MSNs to confirm the reproducibility of the dopamine-dependent plasticity in terms of electrophysiological properties (Figure 3.1.8).

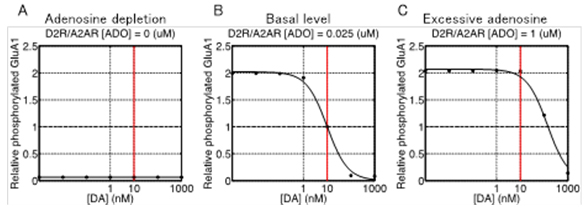
Figure 3.1.7: Dopamine dose-dependent responses of phosphorylation of AMPAR after 500 sec after stimulus onset at three different extracellular adenosine levels (A to C). Horizontal and vertical axes represent input level of dopamine (logarithmic scale) and relative level of phosphorylation scaled to the value at 10 nM when a basal level of adenosine (25 nM), respectively. Dots in each plot are the values obtained by simulation and the solid line is generated by nonlinear regression of the data.

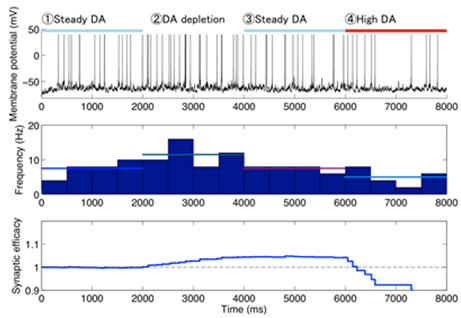
Figure 3.1.8: A typical example of simulated electrophysiological response of (D2R-expressing) MSN to varied dopamine input. Top to bottom figures represent transient membrane potential, firing rate, and corticostriatal synaptic weight of the neuron, respectively. Horizontal bars on the top figure represent the duration of different levels of dopamine input (steady: 10 nM, deprivation: 0 nM, high: 1μM).

3.1.4 Development of a new database platform form phosphoproteomics [Yoshimoto]

Protein phosphorylation plays a crucial role in many intracellular processes that promote (or prevent) the progress of disease and change the excitability of the cells in the context of neural processing. Thanks to recent development in proteomics and genomics, it is predicted that about 500 protein kinases and 650,000 phosphorylated sites exist in human proteins. On the other hand, it is little known what sites are phosphorylated by a specific kinase and what extracellular stimuli activate (or inhibit) the protein phosphorylation via intracellular signaling cascades, which is a fundamental step to reveal the complete picture of signaling pathways of cellular functions. Prof. Kozo Kaibuchi (Nagoya University Graduate School of Medicine) recently developed a new methodology for screening the target phospholyrated sites of a given kinase using the mass spectrometry, and succeeded in identifying hundreds of phosphorylated sites of representative kinases such as PKA, MAPK, CaMKII and so on. Aiming at facilitating to extract scientifically significant information from a bunch of the data, we developed a database platform for phosphoproteomics under the collaboration with Prof. Kaibuchi.

In the database, about 3500 pairs of protein kinases and phosphorylated sites (or proteins) identified by Prof. Kaibuchi’s laboratory as well as about 500 pairs cited from the literature has been registered so far. In order to facilitate the users to associate the data with the signaling pathways, the system provides a graphical user interface to retrieve the data relevant to pathway diagrams (Figure 3.1.9(a)). Also, each of kinases and phosphorylated proteins is associated with links of external databases such as Uniprot KB (proteomics database), HGNC DB (genomics database), HuGE Navigator (human genome epidemiology), enable us to predict unknown functions of the protein phosphorylation with the smallest effort (Figure 3.1.9(b)).

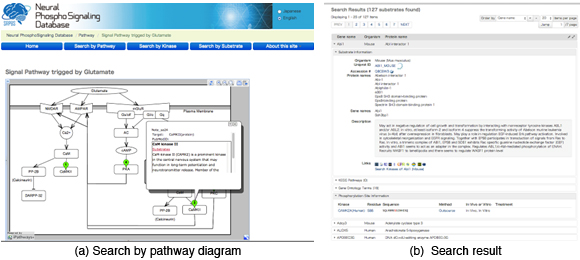
Figure 3.1.9:  Snapshots of features provided by the database. (a) A graphical user interface to retrieve kinases and phosphorylated sites associated with a glutamete signal. (b) The search results corresponding to the options specified by panel (a).

3.2 Systems Neurobiology Group

3.2.1 The role of serotonin in the regulation of patience [Katsuhiko Miyazaki, Kayoko Miyazaki]

While serotonin is well known to be involved in a variety of psychiatric disorders including depression, schizophrenia, autism, and impulsivity, its role in the normal brain is far from clear despite abundant pharmacology and genetic studies. From the viewpoint of reinforcement learning, we earlier proposed that an important role of serotonin is to regulate the temporal discounting parameter that controls how far future outcome an animal should take into account in making a decision (Doya, Neural Netw, 2002).

In order to clarify the role of serotonin in natural behaviors, we performed neural recording, microdialysis measurement and optogenetic manipulation of serotonin neural activity from the dorsal raphe nucleus (DRN), the major source of serotonergic projection to the cortex and the basal ganglia.

So far, we found that the level of serotonin release was significantly elevated when rats performed a task working for delayed rewards compared with for immediate reward (Miyazaki et al., Eur J Neurosci, 2011). We also found many serotonin neurons in the dorsal raphe nucleus increased firing rate while the rat stayed at the food or water dispenser in expectation of reward delivery (Miyazaki et al., J Neurosci, 2011).

To examine causal relationship between waiting behavior for delayed rewards and serotonin neural activity, 5-HT1A agonist, 8-OH-DPAT was directly injected into the dorsal raphe nucleus to reduce serotonin neural activity by reverse dialysis method. We found that 8-OH-DPAT treatment significantly could not wait for long delayed reward (Miyazaki et al., J Neurosci, 2012). These results suggest that activation of dorsal raphe serotonin neurons is necessary for waiting for delayed rewards.

To further investigate whether a timely activation of the DRN serotonergic neurons causes animals to be more patient for delayed rewards, we introduced transgenic mice that expressed the channelrhodopsin-2 variant ChR2(C128S) in the serotonin neurons. We confirmed that blue light stimulation of DRN effectively activate serotonin neurons by monitoring serotonin efflux in the medial prefrontal. We found that serotonin neuron stimulation prolonged the time animals spent for waiting in reward omission trials. This effect was observed specifically when the animal was engaged in deciding whether to keep waiting and not due to motor inhibition. Control experiments showed that the prolonged waiting times observed with optogenetic stimulation were not due to behavioral inhibition or the reinforcing effects of serotonergic activation (Miyazaki et al., Curr Biol, 2014). These results show that the timed activation of serotonin neurons during waiting promotes animals’ patience to wait for delayed rewards.

3.2.2 Dissociation of working memory-based and value-based strategies in a free-choice task [Makoto Ito, Tomohiko Yoshizawa]

Value-based decision strategies, such as Q-learning, has been utilized to analyze the neuronal basis of decision making. The hypotheses that value-based strategies are implemented in the cortico-basal ganglia loops have been supported by substantial studies reporting neural activities correlated with action values. However, animals often show different strategies, such as the win-stay, lose-switch strategy (WSLS); after a rewarded trial, the same action is selected, otherwise other action is selected.

In this study, we hypothesized that WSLS is employed when the working memory (WM) is readily usable and value-based strategy is employed when WM is hard to use. To test our hypothesis, we examined rats’ choice behavior and action signal in a cortical motor-output area, the primary motor cortex (M1), in a free-choice task with WM interference.

The task was started by the presentation of “choice tone” or “no-choice tone”. After choice tone, a rat was required to perform a nose poke into ether left or right hole (choice trials), then a food pellet was delivered probabilistically depending on his choice (e.g., left = 75%, right = 25%). For no-choice tone, rat was required not to perform any nose pokes (no-choice trials).

We compared rats’ choice strategies in the interfere condition (IC), in which no-choice trials were inserted between every choice trial, and the control condition (CC) consisting of only choice trials. The reward probabilities were reversed after several tens of choice trials. In IC, the rats needed several choice trials to adapt to the reversed reward probabilities while the adaptation in CC needed only single trial. The strategy in CC could be explained by WSLS with noise, while action probabilities in IC changed gradually by past experience, consistently with value-based strategy with small learning rate. Before the start of choice action, 39% of neurons (66/169) in M1 coded upcoming action. In 32% of them (21/66), the firing rate immediately before action execution significantly differed between IC and CC (Figure 3.2.2). These results support our hypothesis and suggest that the action command signals generated by WM-based and value-based strategies are differentially coded in M1.

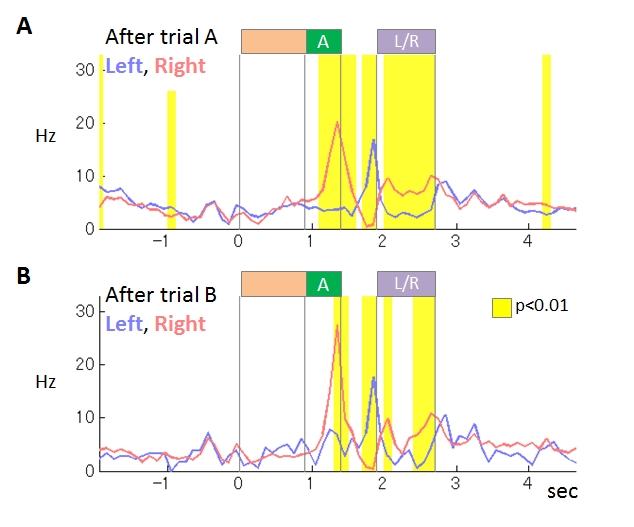
Figure 3.2.2 : An example of M1 neurons coding upcoming action. This neuron showed stronger activity during tone A presentation in right-selected trials than in left-selected trials. The differences of the activity were stronger in the interfere condition (B) than in the control condition (A).

Figure 3.2.3: Rat’s motion tracking during the choice task. (Left) Chamber with 3D motion tracking system. (Center) Rat during the left hole poking. It is attached IR reflection markers on the head, back, and tail. (Right) Reconstructed rat’s posture of left panel.

3.2.4 Investigation of action-dependent state prediction by two-photon microscopy [Funamizu, collaboration with Professor Kuhn]

  In uncertain and changing environments, we sometimes cannot get enough sensory inputs to know the current context, and therefore must infer the context with limited information to make a decision. We call such internal simulation of context a mental simulation. One illustrative example of the mental simulation happens in a game called watermelon cracking, in which a person tries to hit a watermelon far away with his eyes closed with a stick: the person needs to estimate his position based on his actions and sensory inputs, e.g., words from others. To investigate the neural substrate of mental simulation, we use two-photon fluorescence imaging in awake behaving mice which enables us to simultaneously image multiple identified neurons and their activities while the mouse conducts a task.

A mouse was head restrained and maneuvered a spherical treadmill. 12 speakers around the treadmill provided a virtual sound environment. The direction and the amplitude of sound pulses emulated the location of sound source, which was moved according to the mouse’s locomotion on the treadmill. When the mouse reached the sound source and licked a spout, it got a water reward. In some trials, the sound was intermittently omitted: the mouse asked to utilize a mental simulation to reach the sound source.

Calcium is an important second messenger in neurons and an increased calcium concentration is correlated with neuronal activity. For this reason we use a genetically encoded calcium indicator, called G-CaMP, in posterior parietal cortex (PPC) of mice to detect neuronal activities. We could record the activities (i) of more than 500 neurons simultaneously and (ii) of cortical layer 1 to 5 for one hour continuously (Figure 3.2.4). From the population activities in layer 2, we decoded the distance to sound source by the least absolute shrinkage and selection operator (LASSO). LASSO extracted the relevant neurons for distance coding; the neurons were homogeneously distributed in the PPC. Also, the decoder could successfully decode the sound-source distance during no-sound periods. These results suggest that PPC neurons represent and update the distance of sound source not only from present auditory inputs but also by dynamic update of the estimate using an action-dependent state transition model.

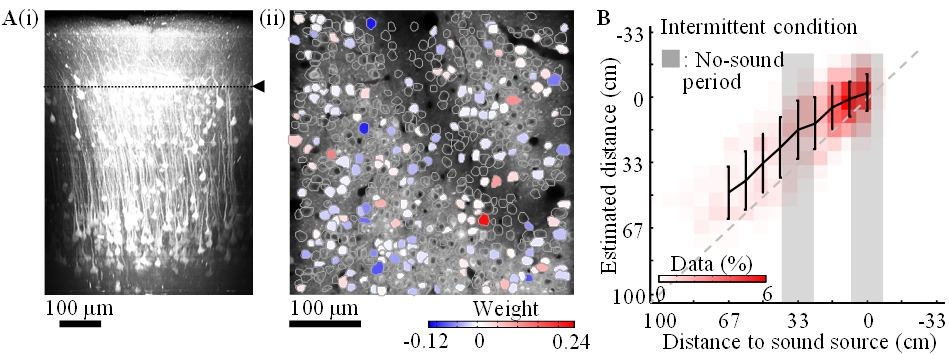
Figure 3.2.4: A-i. In-vivo imaging of neurons with two-photon microscopy. XZ plane reconstruction of calcium sensor expressing cortical neurons in posterior parietal cortex. The dotted line indicates the imaging plane in A-ii. A-ii. Neurons coding sound-source distance. 282 (somata colored red or blue) among 540 neurons were extracted by LASSO. The colors show the weights in LASSO. B. Distance estimation extracted from neuronal activity with LASSO. Horizontal and vertical axes show the actual and estimated distance to sound source, respectively. The estimations were successful even during the no-sound periods in the intermittent condition.

3.3 Adaptive Systems Group

3.3.1 Inverse reinforcement learning using density ratio estimation

Reinforcement Learning (RL) is a computational framework for investigating decision-making processes of both biological and artificial systems that can learn an optimal policy by interacting with an environment. There exist several open questions in RL, and one of the critical problems is how we design and prepare an appropriate reward/cost function. It is easy to design a sparse reward function which gives a positive reward when the task is accomplished and zero otherwise, but that makes it hard to find an optimal policy. In some situations, it is easier to prepare examples of a desired behavior than to handcraft an appropriate reward/cost function. Recently, Inverse Reinforcement Learning (IRL) has been proposed in order to derive a reward/cost function from demonstrator's performance and to implement imitation learning. This study proposes a novel inverse reinforcement learning method based on density estimation under the framework of Linearly solvable Markov Decision Process (LMDP).

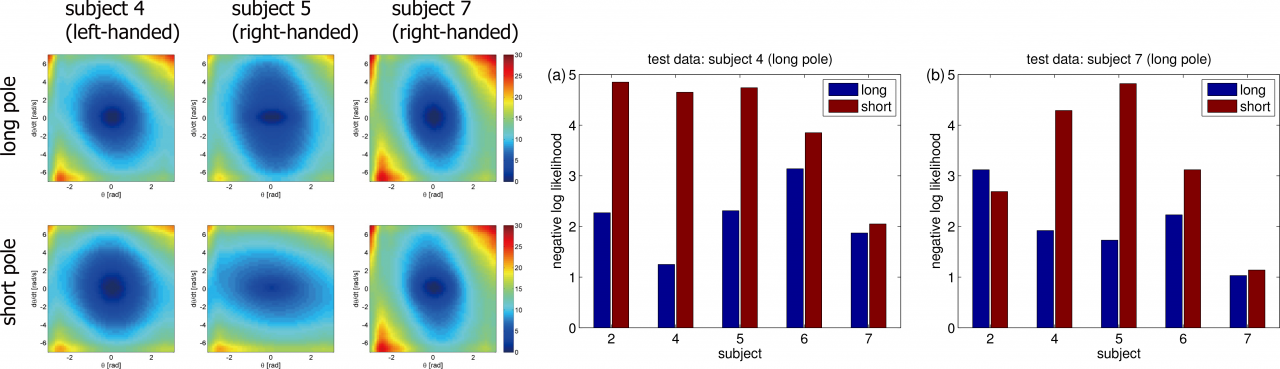
Figure 3.3.1: Experimental results of inverse reinforcement learning. (Left): Estimated cost functions from three subjects. (Middle and Right) Negative log likelihood that evaluates how the reconstructed policy fits the test data.

In LMDP, the logarithm of the ratio between the controlled and uncontrolled state transition densities is represented by the state-dependent cost and the value function. Our proposal is to use density ratio estimation methods to estimate the transition density ratio and the least squares method with regularization to estimate the state-dependent cost and the value function that satisfies the relation. Our method can avoid computing the integral such as evaluating the partition function. A simple numerical simulation of a pendulum swing-up shows its superiority over conventional methods. We further apply the method to humans’ behaviors in performing a pole balancing task and show that the estimated cost functions can predict subjects' performance in new trials or environments. The left panel of the Figure 3.3.1 shows the estimated cost function of some subjects in the short and long pole conditions. For example, the subject 7 used the same cost for the both conditions while the subjects 4 and 5 used the different cost. These facts correspond to the difference of behaviors. The right panel shows the negative log likelihood of the optimal policy trained with the estimated cost function.

3.3.2 Embodied evolution

Polymorphism has fascinated evolutionary biologist since the time of Darwin. Biologist have observed discrete alternative mating strategies in many different species, for both male and females. In this study, we demonstrate that polymorphic mating strategies can emerge in a small colony with hermaphroditic robots, using our earlier proposed framework for performing robot embodied evolution with a limited population size. We used a survival task where the robots maintained their energy levels by capturing energy sources and physically exchanged genotypes for the reproduction of offspring. The reproductive success was dependent on the individuals’ energy levels, which created a natural trade-off between the time invested in maintaining a high energy level and the time invested in attracting potential mating partners. In the experiments, two types of mating strategies emerged: 1) roamers, who never waited for a potential mating partner and 2) stayers, who waited for potential mating and where the waiting threshold depended on their current energy level and sensory inputs. In a majority of the experiments, the emerged populations consisted of individuals executing only one mating strategy. However, in a minority of the simulations, there emerged a evolutionarily stable polymorphic population of roamers and stayers. In one instance, the stayers were split into two subpopulations: stayers who almost always waited for potential mating partners (strong stayers), and stayers who only waited if the energy level was high and an energy source was close (weak stayers). Our analyses show that a population consisting of three phenotypes also could constitute a globally stable polymorphic ESS with several attractors.

Figure 3.3.2: DiFinetti diagram of the directions and magnitudes of the changes in subpopulation proportions for the three phenotypes, strong stayers (SS), weak stayers (WS), and roamers (R). The small blue circles indicate the tested phenotype proportions. The red arrows show the average direction and magnitude of the change in phenotype proportions (magnified by a factor of five for visualization purposes). The green line, starting in the black circle and ending in the black triangle, shows the phenotype proportions in final 20 generations of the evolutionary experiments. The gray-scale coloring visualizes the average population fitness.

3.3.3 Linearly solvable Markov games

In model-based reinforcement learning, an optimal controller is derived from an optimal value (cost-to-go) function by solving the Bellman equation, which is often intractable due to its nonlinearity. Linearly solvable Markov decision process (LMDP) is a computational framework to efficiently solve the Bellman equation by exponential transformation of the value function under a constraint on the action cost function. The major drawback of the LMDP framework is, however, that an environmental model is given in advance. Model learning is integrated with LMDP to overcome the problem for continuous problems reported in FY2012, but the performance of the obtained controllers is critically affected by the accuracy of the environmental model.

One possible way to overcome this problem is to adopt concepts from the robust control theory, which considers the worst adversary and derives an optimal controller using a game theoretic solution. Recently, the framework of the linearly solvable Markov Game (LMG) is proposed as an extension of LMDP by Dvijotham and Todorov, in which the optimal value function is obtained as a solution of the Hamilton-Jacobi-Isaacs (HJI) equation. Since LMG also linearizes the nonlinear HJI equation under similar assumptions of LMDP, an optimal policy can be computed efficiently. While the LMG framework has been shown to promote robustness against disturbances, its advantage over the LMDP framework in the face of modeling errors has not been fully investigated.

In this study, we compare the performances of the LMDP and LMG based controllers in the tasks of grid-world with risky states and swing-up pole. We investigate the robustness of the controllers under variable gaps between the state transition model used for controller design and that of the actual environment. Experimental results in the discrete problem show that the LMG based policy works well by setting the robustness parameter of LMG to the maximum value while the LMDP based policy is very sensitive to the accuracy of the modeling error. On the contrary, experimental results in the continuous problem show that the robustness parameter should be tuned to obtain the best performance in the LMG based policy.

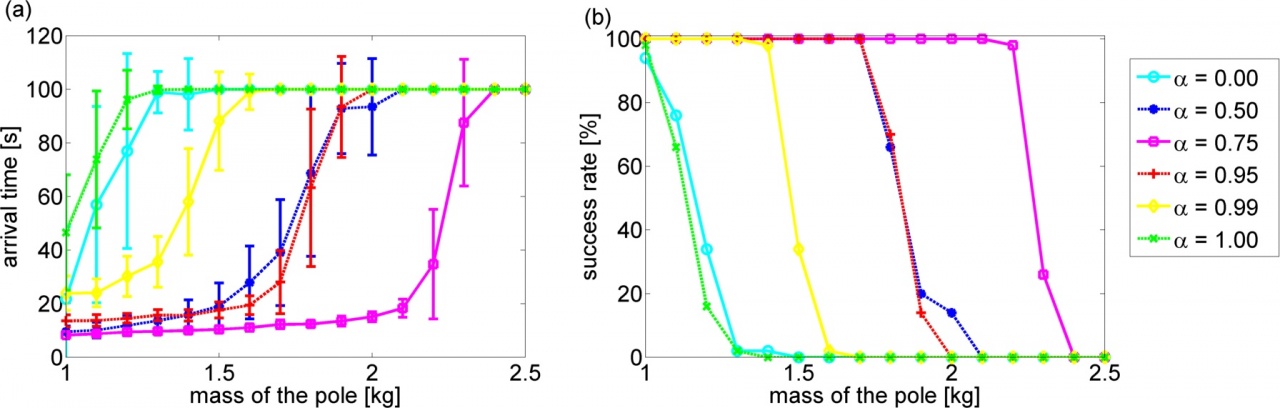
Figure 3.3.3: (a): Arrival time to the desired state. (b): Success rate of swing-up. In each plot, alpha represents the robustness parameter and the horizontal axis is the mass of the pole in test condition.

3.3.4 Smartphone robot projects

Recent smartphones have high computation performance and various sensors in the small body. Therefore various applications of smartphones are proposed in commercial and academic studies. This study proposed and develops a new robot platform using a smartphone, called Smart Phone Robot, aiming the development platform of the home robot in the future.  To achieve this goal, we design a new hardware system for the smartphone robot and propose software architecture necessary for the control application of the robot. Figure 3.3.4 shows our robots. Compared to the robot developed in FY2012, we upgrade the hardware with the Android phone with Nexus 4, an Android compatible interface board, IOIO OTG, the HUB-EE wheels with built-in motor, motor controller and rotary encoder, and a wireless chargeable battery. In addition, the right robot has two elastic bumpers. The robot shell is designed by AUTOCAD and 3D printed out.

Figure 3.3.4: Smartphone mobile robots based on Nexus 4 and IOIO OTG.

Then, we implement the modular control architecture for balancing and standing-up behaviors. For achieving the balancing behavior to stabilize the upright position, we apply the discrete-time Linear Quadratic Regulator (LQR). The system dynamics parameters are identified by the least squares method using the data collected from the real robot experiments. For achieving standing-up behavior from the resting positions, we adopt a sine wave controller as a destabilizing controller. We use two sets of springs at two initial resting positions. We hand-tune the stiffness of the springs as well as the parameters of the switching threshold, the amplitude of the motor output, and the frequency of the sine wave controller to achieve a good performance.

4. Publications 

4.1 Journals 

1. Doya, K. The neural network mechanisms of mental simulation and decision making. Seitai no Kagaku, 64, 297-300 (2013).
2. Elfwing, S. & Doya, K.  Emergence of polymorphic mating strategies in robot colonies. PLoS One. 9(4):e93622. doi: 10.1371/journal.pone.0093622 (accepted)
3. Kinjo, K., Uchibe, E. & Doya, K.  Evaluation of linearly solvable Markov decision process with dynamic model learning in a mobile robot navigation task. Frontiers in neurorobotics 7, 7, doi:10.3389/fnbot.2013.00007 (2013).
4. Nakano, T., Yoshimoto, J. & Doya, K.  A model-based prediction of the calcium responses in the striatal synaptic spines depending on the timing of cortical and dopaminergic inputs and post-synaptic spikes. Frontiers in Computational Neuroscience 7, doi: 10.3389/fncom.2013.00119 (2013).
5. Yoshimoto, J., Ito, M. & Doya, K. Decision-making mechanism of the brain and reinforcement learning. Journal of the Society of Instrument and Control Engineers, 52, 749-754 (2013).

4.2 Books and Other One-Time Publications

Doya, K. & Kimura, M.  The Basal ganglia, Reinforcement Learning, and the Encoding of Value, in Neuroeconomics: Decision making and the Brain, 2nd edition (eds. Paul W. Glimcher & Ernst Fehr), Ch. 17, pages 321-333, Elsevier (2013).

4.3 Oral and Poster Presentations 

1. Doya, K.  Introduction to numerical methods for ordinary and partial differential equations, in Okinawa Computational Neuroscience Course 2013, OIST (2013).
2. Doya, K.  Introduction to reinforcement learning and Bayesian inference, in Okinawa Computational Neuroscience Course 2013, OIST (2013).
3. Doya, K.  Introduction to reinforcement learning and Bayesian inference, in Okinawa Computational Neuroscience Course 2013, OIST (2013).
4. Doya, K.  Neural networks for reinforcement learning, in Francis Crick Symposium on Neuroscience, The Changing Brain, Suzhou Dushu Lake Conference Center, China (2013).
5. Doya, K.  Prediction, confidence, and patience, in International Symposium on Prediction and Decision Making, Kyoto University (2013).
6. Doya, K.  Reinforcement learning, Bayesian inference and brain science, Kyoto University, Kyoto (2013).
7. Doya, K.  Robotics and Neuroscience, in Technologies for Humans and Human Robotics, Italian Institute of Culture (Tokyo) (2013).
8. Doya, K.  The brain's mechanisms for reinforcement learning, Sony City Osaki (Shinagwa, Tokyo) (2013).
9. Doya, K.  The brain's mechanisms for reinforcement learning, University of Tokyo (2014).
10. Doya, K.  Understanding brain functions and dysfunctions by computers, in Hokudai-RIKEN Joint Symposium: Simulation of living body for future medicine, Hokkaido University (2013).
11. Doya, K.  Understanding the mechanisms of the mind by computers: Do robots suffer depression?, in 2013 Hiroshima Symposium for Saving Heart and Life / FY2013 Comprehensive Brain Science Network Public Lecture, Hiroshima (2013).
12. Doya, K. & Yoshimoto, J.  Multi-scale modeling of the brain and the body, in The 91st Annual Meeting of the Physiology Society of Japan, Special Lecture Series in Kagoshima, Current Status of Physiome & Systems Biology: the Efforts in Japan, Kagoshima University (Kagoshima) (2014).
13. Funamizu, A., Kuhn, B. & Doya, K.  Investigation of model-based decision making by two-photon microscopy, in 14th Winter Workshop 2014: Future perspectives of computational brain science, Rusutsu, Hokkaido (2014).
14. Funamizu, A., Kuhn, B. & Doya, K.  Investigation of neuronal activity in the posterior parietal cortex by two-photon microscopy, in International Symposium on Prediction and Decision making, Kyoto University (2013).
15. Funamizu, A., M., I., Doya, K., Knazaki, R. & Takahashi, H.  Role of prefrontal and striatal neurons in task-condition-dependent action selection of rat, in Neuro2013, Kyoto International Conference Center (Kyoto) (2013).
16. Igarash, J.  A prospective of the brain simulation with Exa FLOPS computer from view of a corticothalamic circuit, in Biosuper computing meeting, winter school, Atami haitu in Shizuoka prefecture (2014).
17. Igarashi, J.  Low power consumption of the brain and possibility of simulation of the brain, in Acceleration technical discussion meeting, Fukushima University, Fukushima prefecture (2013).
18. Igarashi, J.  Reproduce the brain with K -Toward treatment of Parkinson's disease, in Gathering for knowing K super computer, Iwate education large hall, Iwate prefecture (2013).
19. Igarashi, J., Shouno, O., Moren, J., Yoshimoto, J., Masumoto, G., Helias, M., Kunkel, S., Morisson, A., Diesmann, M., Fukai, T. & Doya, K.  Presentation Development of a corticothalamic circuit for reproducing Parkinson's disease tremor, in HPCI strategic research program area 1 workshop, AICS in Hyougo Prefecture (2014).
20. Ito, M.  Models of decision making and information representation in the basal ganglia, Ritsumeikan University (Kusatsu, Shiga) (2013).
21. Ito, M. & Doya, K.  Hierarchical coding in the striatum during a free-choice task, in Neuro2013, Kyoto International Conferece Center (Kyoto) (2013).
22. Ito, M. & Doya, K.  Hierarchical population coding of trial phases by the striatal neurons during a choice task, in Society for neuroscience annual meeting, San Diego, USA (2013).
23. Ito, M. & Doya, K.  Hierarchical representation of trial phases in the dorsolateral striatum, the dorsomedial striatum, and the ventral stratum during a choice task, in Internal symposium on prediction and decision making 2013, Kyoto, Japan (2013).
24. Miyazaki, K., Miyazaki, K. W., Tanaka, K. F., Yamanaka, A., Takahashi, A. & Doya, K.  Optogenetic activation of dorsal raphe serotonin neurons enhances patience for future rewards, in Optogenetics 2013, Keio University Tokyo (2013).
25. Miyazaki, K., Miyazaki, K., Tanaka, K., Yamanaka, A., Takahashi, A. & Doya, K.  Optogenetic activation of dorsal raphe serotonin neurons enhances patience for future rewards, in The 87th Anuual Meeting of the Japanese Pharmacological Society, Sendai, Miyagi (2014).
26. Miyazaki, K., Miyazaki, K., Tanaka, K., Ymanaka, A., Takahashi, A. & k, D.  Optogenetic activation of dorsal raphe serotonin neurons enhances patience for future rewards, in Society for Neuroscience Annual Meeting, San Diego, USA (2013).
27. Moren, J., Igarashi, J., Shouno, O., Yoshimoto, J. & Doya, K.  Toward Closing the Loops on Integrated Cortical-Basal Ganglia-Thalamus Models, in HPCI strategic research program area 1 workshop, RIKEN AICS(Kobe, Hyogo) (2014).
28. Oba, S., Nakae, K. & Yoshimoto, J.  On cross-correlogram analysis of multi-neuronal spike-train data based on dynamic causal modeling, in The 34th Workshop on IPSJ Special Interest Group Meeting on Bioinformatics and Genomics, OIST (2013).
29. Ota, S., Uchibe, E. & doya, K.  Analysis of human behaviors by inverse reinforcement learning in a pole balancing task, in 3rd International Symposium on The Biology of Decision Making, Paris, France (2013).
30. Otsuka, M., Yoshimoto, J. & Doya, K.  A stochastic parameter estimation method for spiking neural networks with the replica exchange Monte Carlo scheme coupled with the NEST simulator, in Neuro2013, Kyoto (2013).
31. Shimizu, Y., Yoshimoto, J., Toki, S., Takamura, M., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K.  Diagnosis of Depression by means of Group L1 regularized logistic regression of fMRI Data, in Neruo2013, Kyoto International Conference Center (Kyoto) (2013).
32. Shimizu, Y., Yoshimoto, J., Toki, S., Takumura, M. Y., S, Okamoto, Y., Yamawaki, S. & Doya, K.  Group LASSO for the Classification of Depression Related fMRI Data, in 14th Winter Workshop 2014: Future perspectives of computational brain science, Rusutsu, Hokkaido (2014).
33. Tanaka, T., Sakuma, T., Misawa, H., Miyashita, Y. & Doya, K.  A study of the driving pleasure based on the evaluation grid method and the reinforcement learning model- An analysis of driver's KANSEI structure and development of a driver model for vehicle dynamics evaluation -, in JSAE 2013 Annual Congress- Autumn, Nagoya Congress Center (2013).
34. Tokuda, T., J., Y., Shimizu, Y., Toki, S., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K.  Multiple clustering analysis of resting-state fMRI data: Toward elucidating the pathophysiology of depression, in Comprehensive Brain Science Summer Workshop 2013 Nagoya (2013).
35. Tokuda, T., Yoshimoto, J., Shimizu, Y., Toki, S., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K.  Data-dimension reduction using multiple Gaussian clustering: Application to resting state fMRI, in NIPS 2013 Workshop on Machine Learning for Clinical Data Analysis and Healthcare, Lake Tahoe, Nevada, USA (2013).
36. Tokuda, T., Yoshimoto, J., Shimizu, Y., Yoshida, K., Toki, S., Takamura, M., Yamamoto, T., Yoshimura, S., Okamoto, Y., Yamawaki, S., Yahata, N. & Doya, K.  Bayesian co-clusgtering analysis of resting-state MRI data: Toward elucidating the pathophysiology of depression, in 14th Winter Workshop 2014: Future perspectives of computational brain science, Rusutsu, Hokkaido (2014).
37. Uchibe, E.  Inverse reinforcement learning for understanding human behaviors, in International Symposium on Past and Future Directions of Cognitive Developmental Robotics, Osaka University Nakanoshima Center 10F (2013).
38. Uchibe, E. & Doya, K.  Combining learned controllers to achieve new goals based on linearly solvable MDPs, in Neuro2013, Kyoto International Conference Center (Kyoto) (2013).
39. Uchibe, E. & Doya, K.  Presentation Inverse reinforcement learning by density ratio estimation, in The 16th Information-Based Induction Sciences Workshop, Tokyo Institute of Technology (2013).
40. Uchibe, E., Elfwing, S. & Doya, K.  Scaled free-energy based reinforcement learning for robust and efficient learning in high-dimensional state spaces, in Neuro 2013, Kyoto International Conference Center (Kyoto) (2013).
41. Uchibe, E., Ota, S. & Doya, K.  Inverse reinforcement learning for analysis of human behaviors, in The 1st Multidisciplinary Conference on Reinforcement Learning and Decision Making, Princeton University, New Jersey, USA (2013).
42. Wang, J., Uchibe, E. & Doya, K.  Standing-up and Balancing Behaviors of Android Phone Robot -- Control of Spring-attached Wheeled Inverted Pendulum --, in IEICE Technical Committee on Nonlinear Problems (NLP), City University of Hong Kong (2013).
43. Yoshida, K., Shimizu, Y., Yoshimoto, J., Toki, S., Takamura, M., Okamoto, Y., Yamawaki, S. & doya, K.  fMRI data analysis with L1-regularized logistic regression considering functional locality of the brain, in The 34th Workshop on IPSJ Special Interest Group Meeting on Bioinformatics and Genomics, OIST (2013).
44. Yoshida, N., Uchibe, E. & Doya, K.  Reinforcement Learning with State-Dependent Discount Factor, in The 3rd Joint IEEE International Conference on Development and Learning and on Epigenetic Robotics, Osaka City Central Public Hall (Osaka) (2013).
45. Yoshimoto, J.  Computational Approach to Neural Basis for Emotional System in SIG-FPAI, Miyakojima, Okinawa (2014).
46. Yoshimoto, J.  Multi-modal approaches to visualizing depression: Toward establishment of objective diagnosis for depression based on machine learning, in Symposia in the 77th Convention of Japanese Psychological Association Sapporo, Japan (2013).
47. Yoshimoto, J. & Ito, M.  Multilateral approached to elucidating neural basis for reward-based learning, in Simposium on Dreams and Future of Reinforcement Learning, Aoyama Gakuin University, Tokyo, Japan (2013).
48. Yukinawa, N., Doya, K. & Yoshimoto, J.  A signal transduction model for adenosine-induced indirect corticostriatal plasticity, in Computational and Systems Neuroscience (Cosyne) 2014, Salt Lake City, USA (2014).

5. Intellectual Property Rights and Other Specific Achievements

Nothing to report

6. Meetings and Events

6.1 Research Visit

• Date: April 15, 2013- September 13, 2013
• Yoshimasa Kubo,  Future University-Hakodate
• Other remarks: Internship Student

• Date: October 1, 2013- December 27, 2013
• Valentin CHURAVY,  University of Osnabrück
• Other remarks: Internship Student

6.2 Joint workshop：Neuro-Computing and Bioinformatics

• Date: June 27-28, 2013
• Venue: OIST Capmpus, Semiar Room B250
• Co-organizers:
  • The Institute of ElectronicsInformation and Communication Engineers(IEICE)
  • Information Processing Society of Japan
  • IEEE Computational Intelligence Society Japan Chapter
  • Japan Neural Network Society
• Speaker:
  • Dr. Mitsuo Kawato, ATR , Advanced Telecommunications Research Institute International. 

6.3 International Symposium on Prediction and Decision Making

• Date: October 13-14, 2013
• Venue: Shiran Kaikan, Faculty of Medicine Campus, Kyoto University
• Grant-in-Aid for Sciencetific Research on Innovative Areas, MEXT, JAPAN
  Elucidation of the Neural Computation for Prediction and Decision Making
• Speaker:
  • Dr. Kenji Doya, OIST
  • Dr. Daeyeol Lee, Yale University
  • Dr. Masamichi Sakagami, Tamagawa University
  • Dr. Daphna Shohamy, Columbia University
  • Dr. Paul Phillips, University of Washington
  • Dr. Fumino Fujiyama, Doshisya University Graduate School of Brain Science
  • Dr. Hitoshi Okamoto, KEN Brain Science Institute
  • Dr. Takatoshi Hikida, Graduate School of Medicine and Faculty of Medicine Kyoto University
  • Dr. Fatuel Tecuapetla, Champalimaud Neuroscience Program
  • Dr. Karl Sigmund, Mathematics University of Vienna
  • Dr. Hidehiko Takahashi, Kyoto University Graduate School of Medicine
  • Dr. Masaki Isoda, Kansai Medical University School of Medicine
  • Dr. Hiroyuki Nakahara, RIKEN Brain Science Institute
  • Dr. Adam Kepecs, Cold Spring Harbor Laboratory
  • Dr.Yutaka Komura, National Institute of Advanced Industrial Science and Technology
  • Dr. Masaaki Ogawa, National Institute for Physiological Sciences

6.4 Seminar 

Title: A framework for fitting functions with very sparse data.

• Date: November13, 2013
• Venue:  OIST Campus Lab1. Seminar Room D015
• Speakers: Reza Hosseini, PhD Statistics

• JSPS foreign researcher, Dep. of Mathematical Informatics, University of Tokyo.

Title: How do you (estimate you will) like them apples?  The role of the orbitofrontal cortex in imagining outcomes and changes caused by the use of an addictive drug

• Date: March 18, 2014
• Venue: OIST Campus Center Bldg. Seminar room C210
• Speakers: Dr. Geoffrey Schoenbaum
• Senior investigator of NIDA-Intramural Research Program