FY2012 Annual Report
Neural Computation Unit
Professor Kenji Doya
Abstract
The Neural Computation Unit pursues the dual goals of developing robust and flexible learning algorithms and elucidating the brain’s mechanisms for robust and flexible learning. Our specific focus is on how the brain realizes reinforcement learning, in which an agent, biological or artificial, learns novel behaviors in uncertain environments by exploration and reward feedback. We combine top-down, computational approaches and bottom-up, neurobiological approaches to achieve these goals. The major achievements of the three subgroups in this fiscal year 2012 are the following.
a) The Dynamical Systems Group is developing machine learning methods for subtype identification and diagnosis of depression patients using functional MRI and other neurobiological data. The group is also developing a large-scale spiking neural network model of the basal ganglia to understand the symptoms of Parkinson's disease. In collaboration with Prof. Kaibuchi's lab in Nagoya U, a database of phosphoproteomics is being created for comprehensive understanding dopamine-related signaling pathways.
b) The Systems Neurobiology Group revealed that pharmacological inhibition of serotonin neurons in the dorsal raphe nucleus increased rats' errors in waiting for delayed rewards and their optogenetic activation facilitates waiting for delayed rewards. Through neural recording and analysis of the ventral, dorso-medial, and dorso-lateral striatum of rats, the group clarified that these three areas encode coarse-to-fine grain events during a behavioral episode. In collaboration with Prof. Kuhn, the group performed two-photon imaging of mice's parietal and premotor cortical neurons in order to elucidate the neural substrates of mental simulation.
c) The Adaptive Systems Group demonstrated in robot experiments that composition of new action policy from pre-learned policies can be realized in the framework of linearly solvable Markov decision process (LMDP). Regarding the free enrgy-based reinforcement learning (FERL), the group showed that a proper scaling of the action value function to the free energy of the restricted Boltzmann machine can drastically improve the performance. A new reinforcement learning framework using state-dependent temporal discount factor was developed and its utility was tested in benchmark simulations.
1. Staff
- Dynamical Systems Group
- Dr. Junichiro Yoshimoto, Group Leader
- Dr. Makoto Otsuka, Researcehr
- Osamu Shouno, Guest Researcher
- Dr. Jan Moren, Researcher
- Systems Neurobiology Group
- Dr. Makoto Ito, Group Leader
- Dr. Akihiro Funamizu, JSPS Research Fellow
- Dr. Katsuhiko Miyazaki, Researcehr
- Dr. Kayoko Miyazaki, Researcher
- Dr. Yu Shimizu, Researcher
- Dr. Tomoki Tokuda, Researcher
- Ryo Shiroishi, Graduate Student
- Adaptive Systems Group
- Dr. Eiji Uchibe, Group Leader
- Dr. Stefan Elfwing, Researcher
- Ken Kinjo, Graduate Student
- Naoto Yoshida, Guraduate Student
- Jiexin Wang, Graduate Student
- Administrative Assistant / Secretary
- Emiko Asato
- Kikuko Matsuo
2. Collaborations
- Theme: The research of biologically-inspired reinforcement learning systems for human-centered interface intelligence of future machines
- Type of collaboration: Joint research
- Researchers:
- Masato Hoshino, Honda Research Institute Japan Co., Ltd
- Osamu Shouno, Honda Research Institute Japan Co., Ltd
- Hiroshi Tsujino, Honda Research Institute Japan Co., Ltd
3. Activities and Findings
3.1 Dynamical Systems Group
Automatic diagnosis and subtype discovery of depressive disorder based on fMRI recordings and machine learning [Shimizu, Tokuda, Yoshimoto]
Diagnosis of depression is currently based on patients' reports on depressive mood and loss of motivation. In the search for an objective and more efficient method to diagnose this complex disease, we are developing machine learning moethods to classify depression patients and healthy controls and to identify sub-types of depression patients.
For classification of depressiona patients, we apply L1-regularized logistic regression of functional magnetic resonance imaging (fMRI) data. Our collabrators in Hiroshima Univeristy collected fMRI data in a semantic verbal fluency task of 20 severely depressed patients and 39 healthy controls. After processing of the data by SPM8, the Z-scores for each voxel were used for binary classification by logistic regression with L1-reguralized constraints, which is referred to as Least Absolute Shrinkage and Selection Operator (LASSO).
The algorithm achieved good classification performance (specificity: 83.0%, sensitivity 87.5% and F-score: 86.0% in 10-fold cross-validation), where the main contributing brain areas were left precuneus, superior and mid temporal lobe, left Thalamus and left superior parietal area (Fig. 1).
Figure 1: Brain areas mainly contributing to depression-control classification. They are identified by the logistic regression analysis with LASSO.
Furthermore, we aimed to identify subtypes of depressive disorders by unsupervised learning from biological data. For this purpose, we developed a Bayesian co-clustering method that takes into account structures in the feature variables.
Fig. 2 shows a data matrix, where subject and feature wise values are arranged in rows and columns, respectively. Traditional clustering methods attribute subjects with similar feature patterns to the same cluster (i.e. group) (Fig. 2a), while our co-clustering method categorizes not only subjects, but also features. The categorization occurs simultaneously (Fig. 2b). This approach has the advantage that in addition to the subject-cluster structure, a feature-cluster structure can be revealed in a data-driven way.
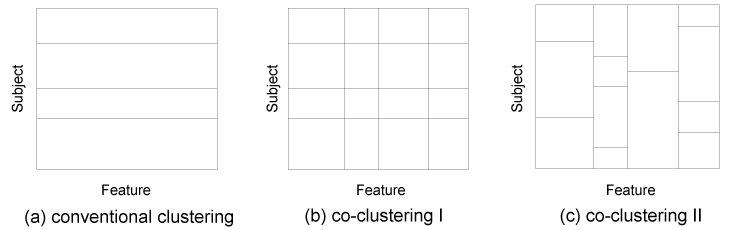
Figure 2: Illustration of the difference between conventional clustering and co-clustering
We applied this co-clustering method to a clinical dataset comprising several questionnaires and blood markers (68 healthy and 45 depressed subjects). For the subjects, we found that our method separated them into four clusters: The first and second (subject-) clusters consisted of healthy subjects only; the third of only severely depressed subjects; the fourth showed a mixture of healthy and mildly depressed subjects (Fig. 3). With respect to feature-clustering, the method revealed five distinct clusters in which features show similar co-variance for all subjects.

Figure 3: Co-clustering result for a clinical dataset that includes several questionnaires and blood markers (68 healthy and 45 depressed subjects). The subject IDs “Cont” and “Dep” indicate control subjects and depression patients, respectively.
We further considered a more general co-clustering model by allowing for different subject-cluster structures in each feature-cluster (Fig. 2c). This extension, called multiple clustering, can implicitly capture correlations between features within the same feature-cluster. More importantly, it can be used as a dimension reduction method that projects high-dimensional data to low-dimensional space in which each dimension represents a feature-cluster found in the high dimensional data by its mean value (hence, one-to-many correspondence between new dimension and features of the original data).
Multiple clustering was applied to resting state fMRI data recorded from 86 healthy and 47 depressed subjects, resulting in compressing the original feature space into only 16-dimensional sub-space (Fig. 4). Next, we identified significant dimensions by applying sample U-test to each dimension to test differences between healthy and depressed subjects. The results revealed following brain areas as relevant to depression-control classification: anterior cingulate cortex, precuneus, amygdala, caudate, and orbital frontal cortex, all of which are included in default mode network (DMN) or reward system.
Figure 4: Co-clustering summary on statistical analysis of resting-state fMRI data by multiple clustering
Large-scale modeling of basal ganglia circuit [Otsuka, Shouno, Moren, Yoshimoto]
The basal ganglia play an important role in motor control and learning, and its dysfunction is associated with movement disorders. The most notable is Parkinson's disease, which involves degeneration of dopaminergic system in the substantia nigra pars compacta (SNc), but it is still unclear how the degeneration changes the dynamics in the basal ganglia circuit, leading to resting tremor and muscle rigidity. To reveal the mechanism in the system level, we aim to construct a realistic model of the basal ganglia circuit.
We based our work on a model proposed by Shouno et al. (IBAGS, 2009) coded by NEST (NEural Simulation Tool) and changed the short-term plasticity rule for the synaptic connections between subthalumic neuclei (STN) and globus pallidus external segments (GPe). This suppressed the intrinsic beta-band oscillation in the normal state (Fig.5). We also scaled up the model to larger size and conducted trial simulation of the model in the K computer.
A common problem in such large-scale neural network models is its parameter tuning for reproducing experimental data. In an effort to develop a theoretically sound methodology for this issue, we also developed a parameter estimation tool that copes with high-dimensional parameter space and the probabilistic distribution of neuronal behaviors. In this method, we assume that a desired behavior of the simulation model is given as a probability distribution of the statistics of spikes emitted by the neurons. The typical example is an empirical distribution of mean firing rates of individual neurons recorded in experiments. The model parameters are estimated so as to minimize the Kullback-Leibler divergence (KLD) between this desired distribution and an empirical distribution obtained by model simulations. To implement the method, we introduced the replica exchange Monte Carlo method combined with highly parallelized simulations by NEST.
Figure 5: Simulation results of our revised model for the basal ganglia network.
Development of the phosphoproteomics database system [Yoshimoto]
Phosphorylation of proteins is a critical biochemical process that changes the properties of the neurons. We start a project to develop the database system from which we can easily find target substrates of a specific kinese. The project is carried out under “Bioinformatics for brain sciences” founded by the Strategic Research Program for Brain Sciences by the Ministry of Education, Culture, Sports, Science and Technology of Japan: More information is avaiable at http://brainprogram.mext.go.jp/missionG/.
3.2 Systems Neurobiology Group
The role of serotonin in the regulation of patience [Katsuhiko Miyazaki, Kayoko Miyazaki]
While serotonin is well known to be involved in a variety of psychiatric disorders including depression, schizophrenia, autism, and impulsivity, its role in the normal brain is far from clear despite abundant pharmacology and genetic studies. From the viewpoint of reinforcement learning, we earlier proposed that an important role of serotonin is to regulate the temporal discounting parameter that controls how far future outcome an animal should take into account in making a decision (Doya, Neural Netw, 2002).
In order to clarify the role of serotonin in natural behaviors, we performed rat neural recording and microdialysis measurement from the dorsal raphe nucleus (DRN), the major source of serotonergic projection to the cortex and the basal ganglia.
So far, we found that the level of serotonin release was significantly elevated when rats performed a task working for delayed rewards compared with for immediate reward (Miyazaki et al., Eur J Neurosci, 2011). We also found serotonin neurons in the dorsal raphe nucleus increased firing rate while the rat stayed at the food or water dispenser in expectation of reward delivery (Miyazaki et al., J Neurosci, 2011).
To examine causal relationship between waiting behavior for delayed rewards and serotonin neural activity, 5-HT1A agonist, 8-OH-DPAT was directly injected into the dorsal raphe nucleus to reduce serotonin neural activity by reverse dialysis method. We found that 8-OH-DPAT treatment significantly imparied the rats in waiting for long delayed reward (Miyazaki et al., J Neurosci, 2012). The result suggests that activation of dorsal raphe serotonin neurons is necessary for waiting for delayed rewards.
To further investigate whether a timely activation of the DRN serotonergic neurons causes animals to be more patient for delayed rewards, we introduced transgenic mice that expressed the channelrhodopsin-2 variant ChR2(C128S) in the serotonin neurons. We confirmed that blue light stimulation of DRN effectively activate serotonin neurons by monitoring serotonin efflux in the medial prefrontal cortex. Serotonin neuron stimulation reduced waiting errors in delayed reward trials and prolonged the waiting time before abandoning in reward omission trials. These results showed that timely activation of serotonin neurons during waiting promotes the animals’ patience for delayed rewards.
Hierarchical population coding of trial phases by the striatal neurons during a choice task [Ito]
The striatum is a major input site of the basal ganglia that takes an essential role in decision making. Recent imaging and lesion studies have suggested that the sub-areas of the striatum have distinct roles.
We recorded neuronal activities from the dorsolateral striatum (DLS, n=190), the dorsomedial striatum (DMS, n=105), and the ventral striatum (VS, n=119) of rats performing a choice task. In this task, when a rat poked into the center hole, one of three cue tones was presented. The rat was required to keep nose-poking during the tone presentation and then to poke either the left or right hole after the offset of the tone. A food pellet was delivered probabilistically depending on the presented tone and the selected poking.
Our previous analysis found that each striatal neuron had a distinct activity pattern (multiple activity peaks through a trial), and that the firing rates at those peaks were modulated by the state (cue tones), the chosen action, the acquired reward, and the reward probability. Here we consider a hypothesis that the variety of activity patterns of a population of striatal neurons encode which phase of what trial a rat is currently in, which can be used for reward prediction, action selection, and learning.
The recorded neuronal spikes in all trials were piece-wise linearly mapped to a standard trial duration of 8.0s so that the times of key task events (the onsets and offsets of the nose poking and the cue tones) match those of the standard trial. Seven trial epochs were defined as the periods between neighboring task events. Each trial epoch was divided into 4 to 20 trial phases of 100ms time period. One trial consists of 80 trial phases.
We randomly sampled 100 neurons from each subarea and estimated the trial phases from their population activities by a non-parametric Bayesian method. The prediction accuracy was evaluated for a new data set which was not used to make a prediction model (cross validation).
In all subareas, the predictions of all 80 trial phases were significantly higher than the chance level (1/80 = 0.0125) (Figure 6). While the average of the prediction accuracy of trial phases was the highest in DLS (DLS: 0.19, DMS: 0.16, VS: 0.10), the average of the prediction accuracy of the trial epochs was the highest in DMS (DLS: 0.71, DMS: 0.76, VS: 0.66). In VS, only the prediction of the reward epoch, after the left- or right- nose poking, is the best in the subareas.
These results support our hypothesis that activity patterns of striatal neurons encode the trial epochs with population coding. Increasingly finer coding of trial phases in VS, DMS, and DLS suggests a hierarchical representation of the progress of a trial in the striatum.
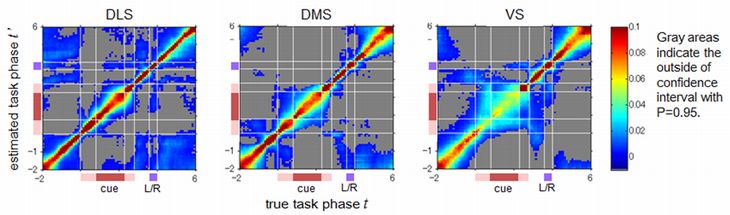
Figure 6: Predictions of trial phases from 100 neurons in DLS, DMS, and VS. The estimated posterior probabilities of trial phases for a correct trial phases are represented by pseudo color.
Imaging the neural substrate of mental simulation by two-photon microscopy [Funamizu, Shroishi, collaboration with Dr. Kuhn]
In model-based planning and precptual decision making in uncertain environments, prediction of environmental state subsequent to past sensory inputs and actions, or mental simulation, plays a ciritical role. To investigate the neural substrate of mental simulation, we use two-photon fluorescence imaging in awake behaving mice which enables us to simultaneously image activities of hundreds of neurons while the mouse conducts a task.
We use a genetically encoded calcium indicator, called G-CaMP, in secondary motor cortex (M2) of mice to detect neuronal activity. Figure 7 shows the two-photon image of neurons labeled with G-CaMP in an anesthetized mouse, indicating that neurons in layer 2/3 were successfully labeled. In preliminary experiments we conducted a simple Pavlovian conditioning task and imaged neuronal activity in awake behaving mice. In this task, mice get a water reward after a tone presentation. We found that layer 2/3 neurons in M2 showed correlated activities with tones, licking, and locomotion, and that such characterized neurons were homogeneously distributed in the recorded areas.

Figure 7: In vivo imaging of neurons by two-photon microscopy. (A, i - iii) layer 2/3 neurons in the xy plane at different depths from the brain surface. (B) a reconstructed view of neurons in the xz plane.
W also examined the neuronal representation of the direction of sound sources in the posterior parietal cortex (PPC), which has been shown to be involved in ego-centric spatial representation.
We monitored the neuronal activity of mice PPC by two-photon calcium imaging during two simple tasks. The first one is a multidirectional sound stimulation task, in which a sound was presented from a random direction of 12 directions (30 degrees apart). The second one is a Pavlovian conditioning task with two-directional sound, in which a sound was presented from one of two directions (45 degree left and 45 degree right) and a reward was given for one direction and not for the other direction.
We found that some neurons in PPC showed significantly different activities in response to different source directions during the sound presentation in both tasks. This result suggests that mouse PPC is involved in the spatial information processing of auditory signals. Examining whether the simulated future sound direction is presented in the PPC will be the next step of our research.
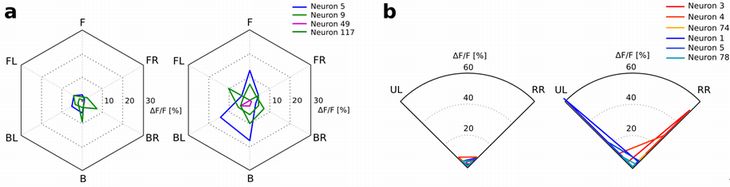
Figure 8: Neural activities measured as fluorescent intensity of calcium indicator in neurons in PPC. a. Mean fluorescent intensities before sound presentation (left diagram) and during sound presentation (right diagram) in the multi-directional sound stimulation task. b. Mean fluorescent intensities before sound presentation (left diagram) and during sound presentation (right diagram) in Pavlovian conditioning with 2 directional sound. F: Front, FR: Front Right, BR: Back Right, B: Back, BL: Back Left, FL: Front Left. RR: Rewarded Right, UL: Unrewarded Left.
3.3 Adaptive Systems Group
Combining multiple behaviors to create a new optimal behavior based on the LMDP framework [Uchibe, Kinjo]
Learning complex behaviors from the scratch requires a lot of trials and compuations. If we can create a new controller by combining learned controllers, learning time can be reduced drastically. However, simple linear combination of controllers is often not appropriate and leads to undesirable behaviors.
Recently, Todorov proposed a class of the so-called Linearly solvable Markov Decision Process (LMDP) which converts a nonlinear Hamilton-Jacobi-Bellman (HJB) equation to a linear differential equation of desirability function, which is a nonlinear transformation of the value function. Linearity of the simplified HJB equation allows us to apply superposition to derive a new composite controller from a set of learned primitive controllers. Todorov proposed a model based method for blending multiple controllers using the model-based LMDP framework. In this framework, mixing weights are naturally designed due to the property of linear differential equation.
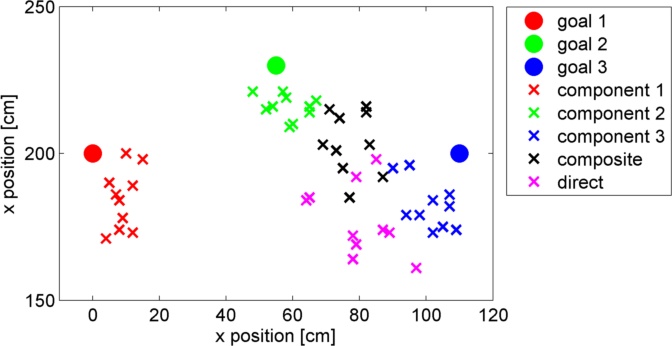
This study proposes a model-free method which is similar to the Least Squares Temporal Difference (LSTD) learning. In this method, the exponentiated cost function can be regarded as the discount factor in LSTD, and a part of the parameters of the desirability function can be shared by primitive controllers. We applied our proposed method to learning walking behaviors with the quadruped robot named “Spring Dog” showin in Figure 9. The task of the robot is to walk from the fixed starting position to the goal position determined by the landmarks. Specifically, the Spring Dog learns to approach one of landmarks in the primitive task. Since there exist three landmarks, three primitive tasks are optimized by the LMDP framework.
Figure 9: Experimental field of the Spring Dog with three landmarks. The top right image represents the view from the Spring Dog. The global coordinate system is also shown in this figure.
Scaled free-energy based reinforcement learning using restricted Boltzmann machines [Elfwing]
Free-energy based reinforcement learning (FERL) was proposed for learning in high-dimensional state- and action spaces, which cannot be handled by standard function approximation methods. In this study, we propose a scaled version of free-energy based reinforcement learning to achieve more robust and more efficient learning performance. The action-value function is approximated by the negative free-energy of a restricted Boltzmann machine, divided by a constant scaling factor that is related to the size of the Boltzmann machine (the square root of the number of state nodes in this study).
Our first task is a digit floor gridworld task, where the states are represented by images of handwritten digits from the MNIST data set. The purpose of the task is to investigate the proposed method’s ability, through the extraction of task-relevant features in the hidden layer, to cluster images of the same digit and to cluster images of different digits that corresponds to states with the same optimal action. We also test the method’s robustness with respect to different exploration schedules, i.e., different settings of the initial temperature and the temperature discount rate in softmax action selection.
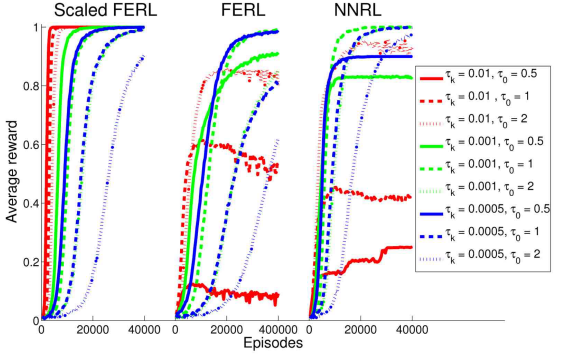
Figure 11: The average reward computed over every 100 episodes and 20 simulation runs, for scaled FERL (left panel), FERL (middle panel), and NNRL (right panel). The line colors correspond to the settings of the parameter of the exploration strategy (red: 0.01, green: 0.001, and blue: 0.0005) and the line types correspond to the setting of the initial parameter of the exploration strategy (solid: 0.5, dashed: 1, and dotted: 2).
Our second task is a robot visual navigation task, where the robot can learn its position by the different colors of the lower part of four landmarks and it can infer the correct corner goal area by the color of the upper part of the landmarks. The state space consists of binarized camera images with, at most, nine different colors, which is equal to 6,642 binary states. For both tasks, the learning performance is compared with standard FERL and with function approximation where the action-value function is approximated by a two-layered feedforward neural network.
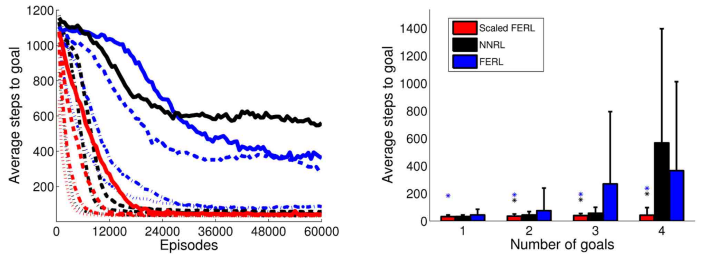
Figure 12: The average number of time steps to goal for the whole learning process (left panel) and in the final 100 episodes (right panel), for the four experiments with 1, 2, 3, and 4 goal areas. The average values were computed over every 100 episodes and 10 simulation runs in each experiment. In the left panel, the line type indicates the number of goals: dotted lines for 1 goal, dash-dotted lines for 2 goals, dashed lines for 3 goals, and solid lines for 4 goals. The colored asterisks in the right panel indicate experiments in which the final average performance of scaled FERL was significantly better (p < 0 . 001) than NNRL (black) or FERL (blue).
Reinforcement learning with state-dependent discount factor [Yoshida, Kinjo]
Conventional reinforcement learning algorithms have several parameters which determine the feature of learning process, called meta-parameters. In this study, we focus on the discount factor that specifies the time scale for resolving the tradeoff between immediate and delayed rewards. Usually, the discount factor is considered as a constant value.
In this study, we introduce a state-dependent discount function and a new optimization criterion for the reinforcement learning algorithm. We first derived a new algorithm for the criterion, named ExQ-learning and showed that the algorithm converges to the optimal action-value function with pobability 1. We then developed a framework to optimize the discount factor and the discount function by using evolutionary algorithm. In order to validate the proposed method, we conducted a simple computer simulation and showed that the proposed algorithm can find an appropriate state-dependent discount function with which the agent performed better than with a constant discount factor.
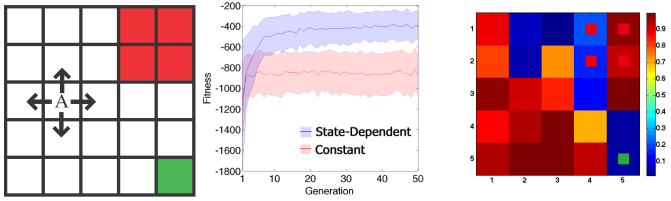
Figure 13: Environment and the results of optimization. Left: The environment used in the simulation. Center: The evolution of the fitness. The horizontal axis is the fitness, the vertical axis is the number of generation. The lines represent the average fitness and the shaded areas represent the standard deviation. Blue represents the result of ExQ-learning (state-dependent discounting) and Red represents that of Q-learning (constant discount factor). Right: The average of the obtained discount function after 50 evolutions. The colors in the figure represent the magnitude of the discount factor at the corresponding state. The colors in small cells are the colors at the corresponding state in the left figure (Red and Green states).
Inverse reinforcement learning to investigate human behavior [Uchibe, Ota]
Reinforcement Learning (RL) is a computational framework for investigating and realizing decision-making processes of both biological and artificial systems that can learn an optimal policy by interacting with an environment. Recently, several methods of Inverse Reinforcement Learning (IRL) have been proposed in order to infer the reward function from the observed behaviors. IRL has been used for extracting the reward function of experts to reproduce opitimal policies in different environments, known as apparenticeship learning. We hypothesized that the variability of people's performance in motor control is due to different choices of reward functions. The aims of the present study are: (1) to identify the reward function from human behaviors in performing a given task, and (2) to elucidate difference of reward functions from multiple subjects and evaluate how it affects their performance. We monitored the behaviors of seven human subjects who tried the task of pole balancing with two different lengths (Fig.14).

Figure 14: Pole balancing task (long pole condition).
We applied inverse reinforcement learning algorithms based on Linearly-solvable Markov Decision Process (LMDP) proposed by Dvijotham and Todorov to infer the reward functions that subjects used. In LMDP the optimal policy is represented by the value function, which is estimated by the maximum likelihood method. Fig.15 shows the cost functions inferred by IRL for three representative subjects and an optimally-designed artificial agent . The axes define the phase space with angle and angular velocity of the pole. The goal state is in the center of the figure at [0, 0]. Since the IRL problem is an ill-posed problem, the true cost function of the artificial agent was not recovered by the IRL algorithm. We found that the value of the estimated cost is smallest at the origin which is regarded as the desired state. In addition, the cost function of huann subjects were asymmetric, which correspond to different habits of human subjects.
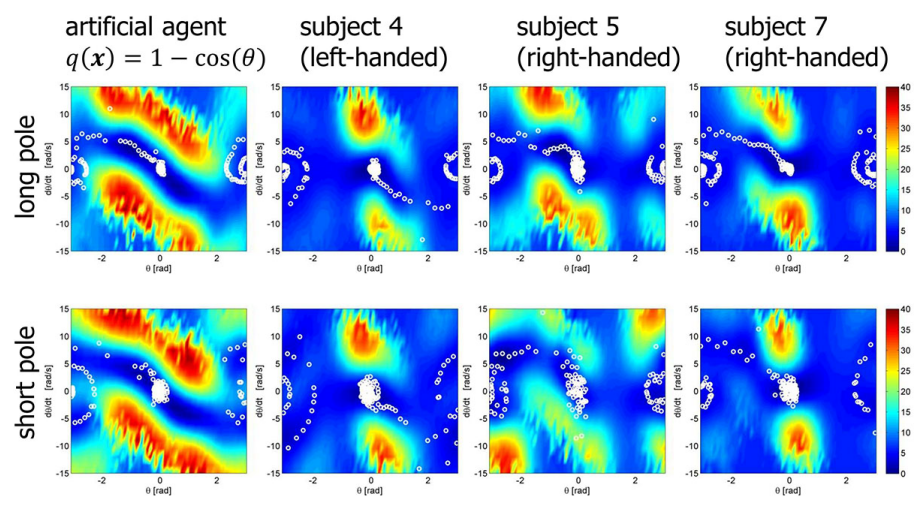
Figure 15: Estimated cost (negative reward) functions in the angle and angular velocity space. Other four state variables are set to 0 for visualization.
Linearity of the optimality equation in LMDP allows us to extract the reward function from the value function efficiently. The shape and parameters of the reward function are used as features for analysis. Our preliminary experimental results suggest that the subjects can be classified by the inferred reward (or cost) functions. As a future study, the analysis of these personalized factors will be applied to help instructing human to improve their performance.
4. Publications
4.1 Journals
Doya, K. & Shadlen, M. N. Decision making. Curr Opin Neurobiol 22, 911-913, doi:10.1016/j.conb.2012.10.003 (2012).
Elfwing, S., Uchibe, E. & Doya, K. Scaled free-energy based reinforcement learning for robust and efficient learning in high-dimensional state spaces. Front Neurorobot 7, 3, doi:10.3389/fnbot.2013.00003 (2013).
Funamizu, A., Ito, M., Doya, K., Kanzaki, R. & Takahashi, H. Uncertainty in action-value estimation affects both action choice and learning rate of the choice behaviors of rats. The European journal of neuroscience 35, 1180-1189, doi:10.1111/j.1460-9568.2012.08025.x (2012).
Miyazaki, K., Miyazaki, K. W. & Doya, K. The Role of Serotonin in the Regulation of Patience and Impulsivity. Molecular Neurobiology 45, 213-224, doi:10.1007/s12035-012-8232-6 (2012).
Miyazaki, K. W., Miyazaki, K. & Doya, K. Activation of Dorsal Raphe Serotonin Neurons Is Necessary for Waiting for Delayed Rewards. The Journal of Neuroscience 32, 10451-10457, doi:DOI:10.1523/JNEUROSCI.0915-12.2012 (2012).
Moren, J., Shibata, T. & Doya, K. The mechanism of saccade motor pattern generation investigated by a large-scale spiking neuron model of the superior colliculus. PLoS One 8, e57134, doi:10.1371/journal.pone.0057134 (2013).
Okamoto, Y., Okada, G., Shishida, K., Fukumoto, T., Machino, A., Yamashita, H., Tanaka, S. C., Doya, K. & Yamawaki, S. Effects of serotonin on delay discounting for rewards--an application for understanding of pathophysiology in psychiatric disorders (in Japanese). Seishin shinkeigaku zasshi = Psychiatria et neurologia Japonica 114, 108-114 (2012).
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
Doya, K. Reinforcement Learning in Robots and the Brain, in IEEE Computational Intelligence Society Chapter Hyderabad Section, Hyderabad, India (2012).
Doya, K. 1. Reinforcement learning and the basal ganglia; 2. Bayesian inference and model-based decision making, in IBRO-UNESCO School on Computational and Theoretical Neuroscience, Hyderabad, India (2012).
Doya, K. Reinforcement learning and science of mind, in Tamagawa University Globall COE Program Open Symposium, Tamagawa University, Tokyo (2012).
Doya, K. Reinforcement learning, basal ganglia, and neuromodulation, Lecture in Computaitonal Neuroscience, Nara Institue of Science and Technology, Ikoma, Nara (2012).
Doya, K. Toward large-scale researh projects, Special Lecture, Okinawa National College of Technology, Nago-shi, Okinawa (2012).
Doya, K. Reinforcement learning, Bayesian inference and brain science, Lecture in Computaitonal Neuroscience, Kyoto University, Kyoto (2012).
Doya, K. From machine learning theory to brain science and psychiatry, Special Lecture in Hiroshima University School of Medicine, Hiroshima (2012).
Doya, K. Closing the loop: simulation of the whole sensory-motor neural network in action, in 4th Biosupercomputing Symposium(ISLiM), Tokyo (2012).
Doya, K. Neural networks for reinforcement learning, Graduate School of Biostudies, Kyoto University Advanced Course in Multicellular Network (2012).
Doya, K. Neural networks for prediction and decision making, in The 6th PRESTO Meeting of the Research Area: Neural Networks, OIST (2012).
Doya, K. 1. Motor control: basal ganglia and motor control 2. Basal ganglia, serotonin, and reward expectation, in Computational and Cognitive Neurobiology Summer School, Beijing, China (2012).
Doya, K. Reinforcement learning and computational neuroscience of decision making, in Autumn School for Computational Neuroscience, Suwa, Nagano (2012).
Doya, K. Neural computation of reinforcement learning, Special Lecture in Nagoya University, Nagoya (2012).
Doya, K. Decision making, learning and rationality, in 45th Annual Meeting of Philosophy of Science Society, Japan, University of Miyazaki, Miyazaki (2012).
Doya, K. The theory of reinforcement learning and the neurobiology of decision making, in JNNS 2012 Symposium neural mechanism for reward-based decision making, Nagoya (2012).
Doya, K. Brain and reinforcement Learning, in 21st Machine Learning Summer School, Kyoto (2012).
Doya, K. Reinforcement learning and the basal ganglia, in CogSci2012: Neural Computations Supporting Cognition: Rumelhart Prize Symposium in Honor of Peter Dayan, Sapporo (2012).
Doya, K. How patient can a mouse be with serotonin stimulation in Tamaga-Caltech joint lecture course: reward and decision making on risk and aversion, Waikoloa beach marriott resort & spa, Hawaii (2012).
Doya, K. Model-free and Model-based Reinforcement Learning, in The 76th Annual Convention of the Japanese Psychological Association, Senshu University, Kawasaki, Kanagawa (2012).
Doya, K. Toward understanding the neural substrate of mental simulation, in Joint Symposium interactive brain dynamics for decision making and communication, Sendai International Center, Sendai, Miyagi (2012).
Doya, K. Brain science after 20 years, The First NINS Colloquium, Hakone, Kanagawa (2012).
Doya, K. Representation of knowledge, in Japanese Cognitive Science Society Summer School, Hakone, Kanagawa (2012).
Doya, K. Multiple strategies for decision making, in SBDM 2012: Second Symposium on Biology of Decision Making, Paris, France (2012).
Doya, K. Neural mechanisms of reinforcement learning, Special Lecture at Peking University, Beijing China (2012).
Doya, K. Tutorial on decision making: from machine learning perspective, in Strategic research on innovative areas"prediction and decision making", Tamagawa University, Machida, Tokyo (2012).
Doya, K. Reinforcement learning algorithm and its neural mechanism, Multi-dimensional brain science training and lecuture, NIPS, Okazaki, Aichi (2013).
Elfwing, S. Scaled free-energy based reinforcement learning for robust and efficient learning in high-dimensional state space, Invited Seminar at The University of Tokyo, Komaba Campus (2013).
Funamizu, A., Ito, M., Kanzaki, R. & Takahashi, H. Value-updating interaction among contexts in choice behaviors of rats, in COSYNE2013, Salt Lake City, U.S.A (2013).
Funamizu, A., Kuhn, B. & Doya, K. Investigation of neuronal activity in secondary motor cortex by two-photon microscopy, in 13th winter workshop: Mechanism of Brain and Mind 2013, Rusutsu, Hokkaido (2013).
Ito, M. Algorithms of decision making based on reward and neuronal representation in the striatum, in Hominization Workshop, Inuyama, Aichi (2012).
Ito, M. Information represented in the basal ganglia during decision making, in JAIST Seminar, Nomi, Ishikawa (2012).
Ito, M. How experience affects: decision making, Super Science Highschool Lecture for World Brain Week, Nara Women's University Secondary School, Nara (2013).
Ito, M. & Doya, K. Presentation Hierarchical representation in the striatum during a choice task, in Comprehensive Brain Science Network Summer Workshop 2012, Sendai, Miyagi (2012).
Ito, M. & Doya, K. Hierarchical representation in the striatum during a free choice task, in 13th Winter Workshop on the Mechanism of Brain and Mind, Rusutsu, Hokkaido (2013).
Kinjo, K., Uchibe, E., Yoshimoto, J., Y. & Doya, K. Learning Motor-visual Dynamics and Solving Linearlized Bellman Equation for Robot Control in Neuro Computing Research Conference, OIST (2012).
Miyazaki, K., Miyazaki, K. W. & Doya, K. The role of serotonin neuron in patience of waiting for delayed rewards, in Serotonin club meeting, Montpellier, France (2012).
Miyazaki, K. W., Miyazaki, K. & Doya, K. Presentation The role of serotonin neuron in patience of waiting for delayed rewards, in Comprehensive Brain Science Network Summer Workshop 2012, Sendai, Miyagi (2012).
Nakano, T., Otsuka, M., Yoshimoto, J. & Doya, K. A spiking neural network model of memory-based reinforcement learning, in INCF Neuroinformatics 2012, Munich, Germany (2012).
Shimizu, Y., Yoshimoto, J. & Doya, K. Machine learning and modelling approaches to depression, in 21st Machine Learning Summer School, Kyoto (2012).
Tokuda, T., J, Y., Shimizu, Y., Takamura, M., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K. Bayesian co-clustering analysis of resting-state MRI data: Toward elucidating the pathophisiology of depression, in 13th winter workshop: Mechanism of Brain and Mind 2013, Rusutsu, Hokkaido (2013).
Yoshida, N., Yoshimoto, J., Uchibe, E. & Doya, K. Development of robot platform with smart phone, in 30th Annual Conference of The Robotics Society of Japan, Sapporo, Hokkaido (2012).
Yoshimoto, J., Shimizu, Y., Tokuda, T., Takamura, M., Yoshimura, S., Okamoto, Y., Yamawaki, S. & Doya, K. Bayesian co-clustering analysis of questionnaire data from normal and depressive subjects, in 13th winter workshop: Mechanism of Brain and Mind 2013, Rusutsu, Hokkaido (2013).
5. Intellectual Property Rights and Other Specific Achievements
Morimura, T., Uchibe, E., Yoshimoto, J., Doya, K. Controller, control algorithm, Director General of Patent Office, Japan 2012
6. Meetings and Events
6.1 Joint Workshop of Neuro-Computing and Bioinformatics
- Date: June 28-29, 2012
- Venue: OIST Campus
- Organizers:
- The Institute of ElectronicsInformation and Communication Engineers(IEICE)
- Information Processing Society of Japan
- IEEE Computational Intelligence Society Japan Chapter
- Japan Neural Network Society
- Speaker:
- Dr. Yoshiyuki Asai (OIST)
6.2 Seminar
- Date: August 22, 2012
- Venue: OIST Campus Lab1
- Speaker: Dr. Tomoki Tokuda (University of Leuven in Belgium)
6.3 Seminar
- Date: August 24, 2012
- Venue: OIST Campus Lab1
- Speaker: Dr. Kenji Morita (The University of Tokyo)
6.4 Seminar
- Date: February 12, 2013
- Venue: OIST Campus Lab1
- Speaker: Dr. Jun Igarashi (RIKEN Brain Science Institute)
6.5 Seminar
- Date: March 11, 2013
- Venue: OIST Campus Lab1
- Speaker: Dr. Hidehiko Takahashi (Kyoto University)
6.6 Seminar
- Date: March 12, 2013
- Venue: OIST Campus Lab1
- Speaker: Dr. Hitoshi Okamoto (RIKEN Brain Science Institute)
6.7 Seminar
- Date: March 29, 2013
- Venue: OIST Campus Lab1
- Speaker: Dr. Kozo Kaibuchi (Nagoya University)
7. Other
Nothing to report.




