Publications & Annual Reports
You can find below a list of recent preprints and publications ordered per year: 2023 and 2022.
In accordance with the institutional requirements, we also provide a more detailed annual report summarizing the activities of the unit for the given year. The reports from this unit can be found in the menu on the left, listed by fiscal year. Annual report links: 2023 and 2022.
Finally, since 2010, OIST provides a centralized site for the annual reports. These reports can be found on the OIST Graduate University's Annual Reports page.
Preprints
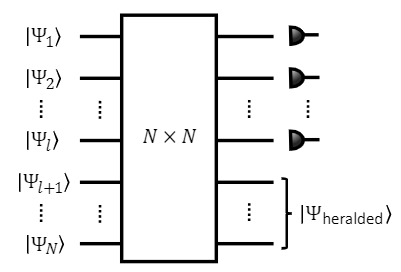
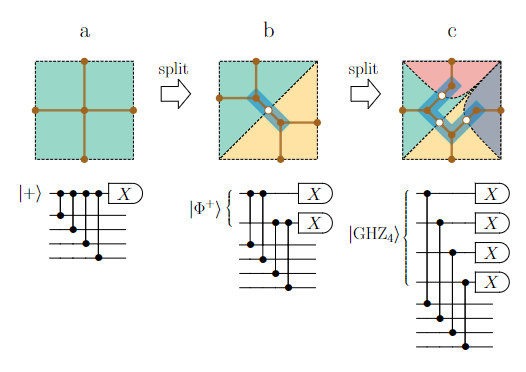
One of the most important resources for quantum optical experiments and applications are on-demand highly entangled multiphoton quantum states. A promising way of generating them is heralding entanglement generation at a high rate from letting independent photons interfere. However, such schemes often work for a specific internal degree of freedom of the interfering photons only. Going to higher numbers of entangled photons, the success probabilities decrease while the number of necessary resources, e.g., auxiliary photons and optical elements, increases. To make probabilistic schemes feasible also for larger quantum states, it is therefore important to find resource-efficient generation schemes with high success probabilities. In this work, we introduce easily implementable schemes to herald qubit Greenberger-Horne-Zeilinger (GHZ) states, higher-dimensional Bell states and higher-dimensional three-party GHZ states. Our schemes solely rely on multiphoton interference, i.e., they can be adjusted to work for arbitrary degrees of freedom. Furthermore, they demonstrate high success probabilities and need comparably few auxiliary photons.
States with negative Wigner function, a significant subclass of non-classical states, serve as a valuable resource for various quantum information processing tasks. Here, we provide a criterion for detecting such quantum states exhibiting negative Wigner function. Our method relies on evaluating moments of the Wigner function which involves computing simple functionals and can be implemented in a real experiment without the need for full state tomography or Wigner function reconstruction. We then provide explicit examples to support our detection scheme. Further, we propose an experimental method utilizing the continuous variable SWAP operator to realize these moments in a real experiment.
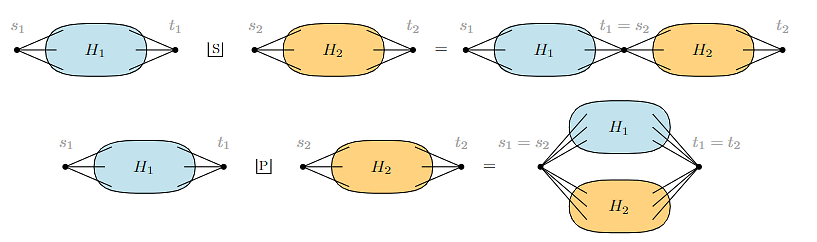
We study the entanglement entropy of a random tensor network (RTN) using tools from free probability theory. Random tensor networks are simple toy models that help the understanding of the entanglement behavior of a boundary region in the ADS/CFT context. One can think of random tensor networks are specific probabilistic models for tensors having some particular geometry dictated by a graph (or network) structure. We first introduce our model of RTN, obtained by contracting maximally entangled states (corresponding to the edges of the graph) on the tensor product of Gaussian tensors (corresponding to the vertices of the graph). We study the entanglement spectrum of the resulting random spectrum along a given bipartition of the local Hilbert spaces. We provide the limiting eigenvalue distribution of the reduced density operator of the RTN state, in the limit of large local dimension. The limit value is described via a maximum flow optimization problem in a new graph corresponding to the geometry of the RTN and the given bipartition. In the case of series-parallel graphs, we provide an explicit formula for the limiting eigenvalue distribution using classical and free multiplicative convolutions. We discuss the physical implications of our results, allowing us to go beyond the semiclassical regime without any cut assumption, specifically in terms of finite corrections to the average entanglement entropy of the RTN.
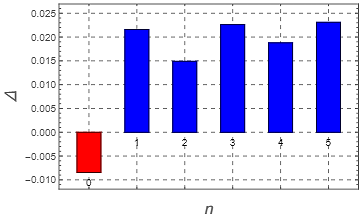
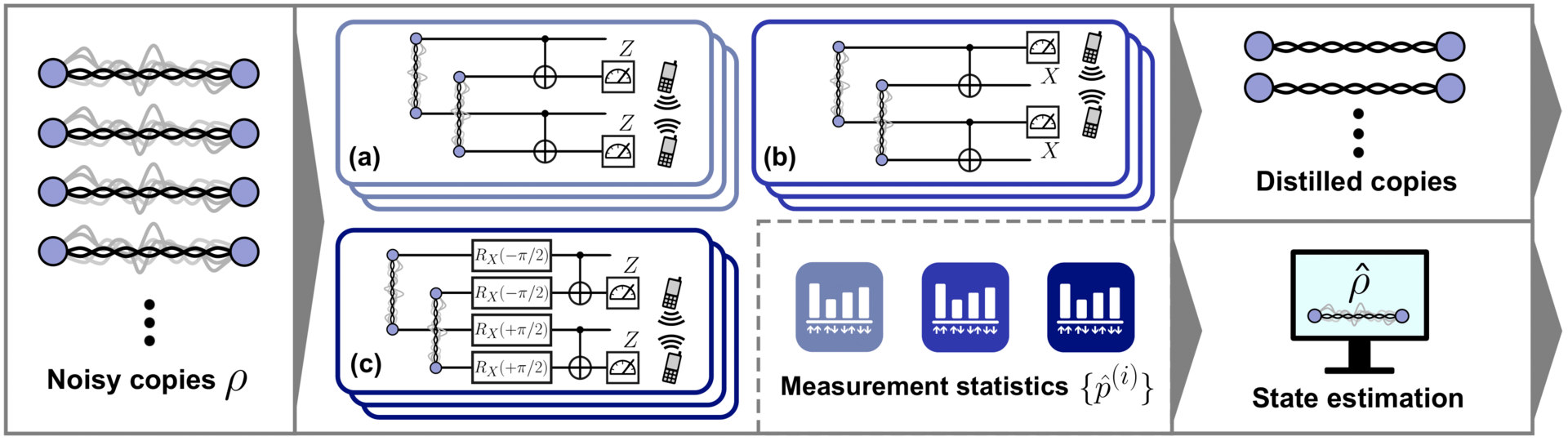
Minimizing both experimental effort and consumption of valuable quantum resources in state estimation is vital in practical quantum information processing. Here, we explore characterizing states as an additional benefit of the entanglement distillation protocols. We show that the Bell-diagonal parameters of any undistilled state can be efficiently estimated solely from the measurement statistics of probabilistic distillation protocols. We further introduce the state estimator `Disti-Mator' designed specifically for a realistic experimental setting, and exhibit its robustness through numerical simulations. Our results demonstrate that a separate estimation protocol can be circumvented whenever distillation is an indispensable communication-based task.
Regarding minimal assumptions, most of classical cryptography is known to depend on the existence of One-Way Functions (OWFs). However, recent evidence has shown that this is not the case when considering quantum resources. Besides the well known unconditional security of Quantum Key Distribution, it is now known that computational cryptography may be built on weaker primitives than OWFs, e.g., pseudo-random states [JLS18], one-way state generators [MY23], or EFI pairs of states [BCQ23]. We consider a new quantum resource, pseudo-entanglement, and show that the existence of EFI pairs, one of the current main candidates for the weakest computational assumption for cryptography (necessary for commitments, oblivious transfer, secure multi-party computation, computational zero-knowledge proofs), implies the existence of pseudo-entanglement, as defined by [ABF+24, ABV23] under some reasonable adaptations. We prove this by constructing a new family of pseudo-entangled quantum states given only EFI pairs. Our result has important implications for the field of computational cryptography. It shows that if pseudo-entanglement does not exist, then most of cryptography cannot exist either. Moreover, it establishes pseudo-entanglement as a new minimal assumption for most of computational cryptography, which may pave the way for the unification of other assumptions into a single primitive. Finally, pseudo-entanglement connects physical phenomena and efficient computation, thus, our result strengthens the connection between cryptography and the physical world.
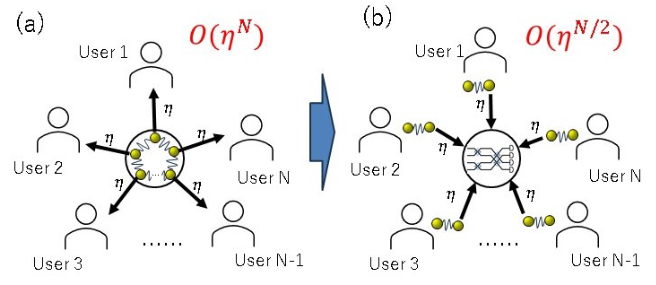
Distributed quantum entanglement plays a crucial role in realizing networks that connect quantum devices. However, sharing entanglement between distant nodes by means of photons is a challenging process primary due to unavoidable losses in the linking channels. In this paper, we propose a simple loss-tolerant protocol for the Greenberger-Horne-Zeilinger state distribution. We analyze the distribution rate under feasible experimental conditions and demonstrate the advantages of rate-loss scaling with respect to direct transmission. Our protocol does not use quantum repeaters and is achievable with current quantum optics technology. The result has direct application to tasks such as conference key agreement or distributed sensing. Moreover, it reduces the requirements for implementing distributed quantum error correction codes such as the surface code.
In this work, we introduce a method to construct fault-tolerant measurement-based quantum computation (MBQC) architectures and numerically estimate their performance over various types of networks. A possible application of such a paradigm is distributed quantum computation, where separate computing nodes work together on a fault-tolerant computation through entanglement. We gauge error thresholds of the architectures with an efficient stabilizer simulator to investigate the resilience against both circuit-level and network noise. We show that, for both monolithic (i.e., non-distributed) and distributed implementations, an architecture based on the diamond lattice may outperform the conventional cubic lattice. Moreover, the high erasure thresholds of non-cubic lattices may be exploited further in a distributed context, as their performance may be boosted through entanglement distillation by trading in entanglement success rates against erasure errors during the error-decoding process. These results highlight the significance of lattice geometry in the design of fault-tolerant measurement-based quantum computing on a network, emphasizing the potential for constructing robust and scalable distributed quantum computers.
In the search for scalable, fault-tolerant quantum computing, distributed quantum computers are promising candidates. These systems can be realized in large-scale quantum networks or condensed onto a single chip with closely situated nodes. We present a framework for numerical simulations of a memory channel using the distributed toric surface code, where each data qubit of the code is part of a separate node, and the error-detection performance depends on the quality of four-qubit Greenberger-Horne-Zeilinger (GHZ) states generated between the nodes. We quantitatively investigate the effect of memory decoherence and evaluate the advantage of GHZ creation protocols tailored to the level of decoherence. We do this by applying our framework for the particular case of color centers in diamond, employing models developed from experimental characterization of nitrogen-vacancy centers. For diamond color centers, coherence times during entanglement generation are orders of magnitude lower than coherence times of idling qubits. These coherence times represent a limiting factor for applications, but previous surface code simulations did not treat them as such. Introducing limiting coherence times as a prominent noise factor makes it imperative to integrate realistic operation times into simulations and incorporate strategies for operation scheduling. Our model predicts error probability thresholds for gate and measurement reduced by at least a factor of three compared to prior work with more idealized noise models. We also find a threshold of 4⋅102 in the ratio between the entanglement generation and the decoherence rates, setting a benchmark for experimental progress.
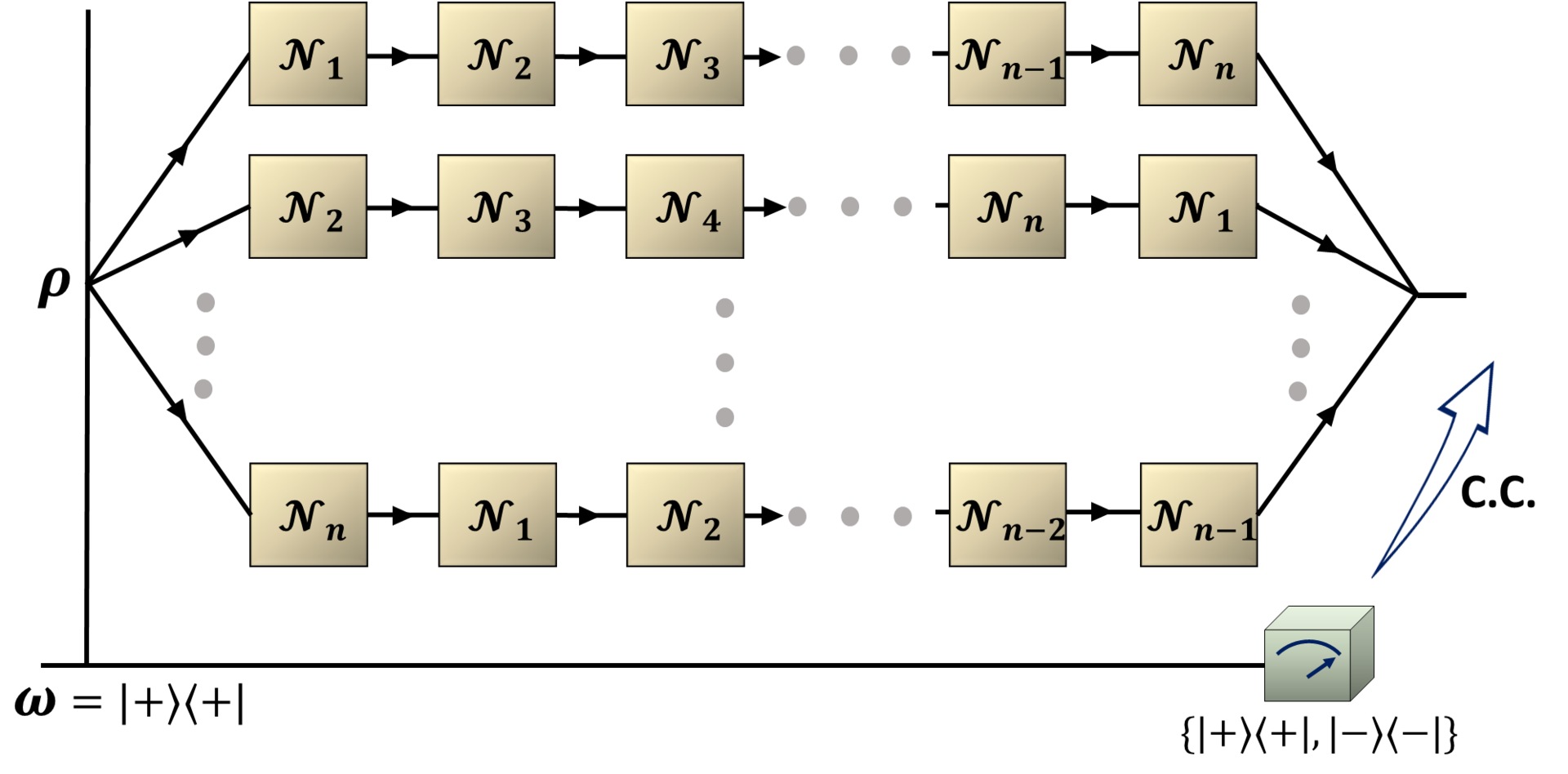
Several recent studies have demonstrated the utility of the quantum SWITCH as an important resource for enhancing the performance of various information processing tasks. In a quantum SWITCH, the advantages appear significantly due to the coherent superposition of alternative configurations of the quantum components which are controlled by an additional control system. Here we explore the impact of increasing the Hilbert-space dimension of the control system on the performance of the quantum SWITCH. In particular, we focus on a quantifier of the quantum SWITCH through the emergence of non-Markovianity and explicitly study their behavior when we increase the Hilbert-space dimension of the control system. We observe that increasing the Hilbert-space dimension of the control system leads to the corresponding enhancement of the non-Markovian memory induced by it. Our study demonstrates how the dimension of the control system can be harnessed to improve the quantum SWITCH-based information processing or communication tasks.
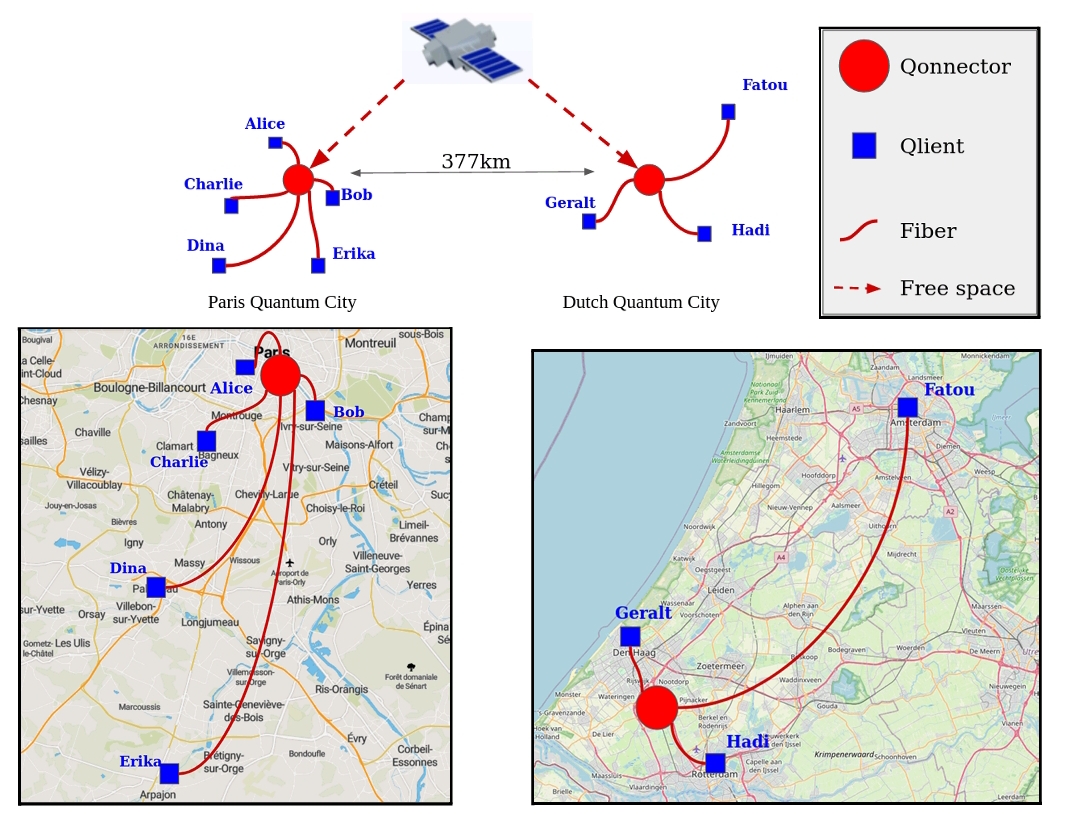
We present and analyse an architecture for a European-scale quantum network using satellite links to connect Quantum Cities, which are metropolitan quantum networks with minimal hardware requirements for the end users. Using NetSquid, a quantum network simulation tool based on discrete events, we assess and benchmark the performance of such a network linking distant locations in Europe in terms of quantum key distribution rates, considering realistic parameters for currently available or near-term technology. Our results highlight the key parameters and the limits of current satellite quantum communication links and can be used to assist the design of future missions. We also discuss the possibility of using high-altitude balloons as an alternative to satellites.
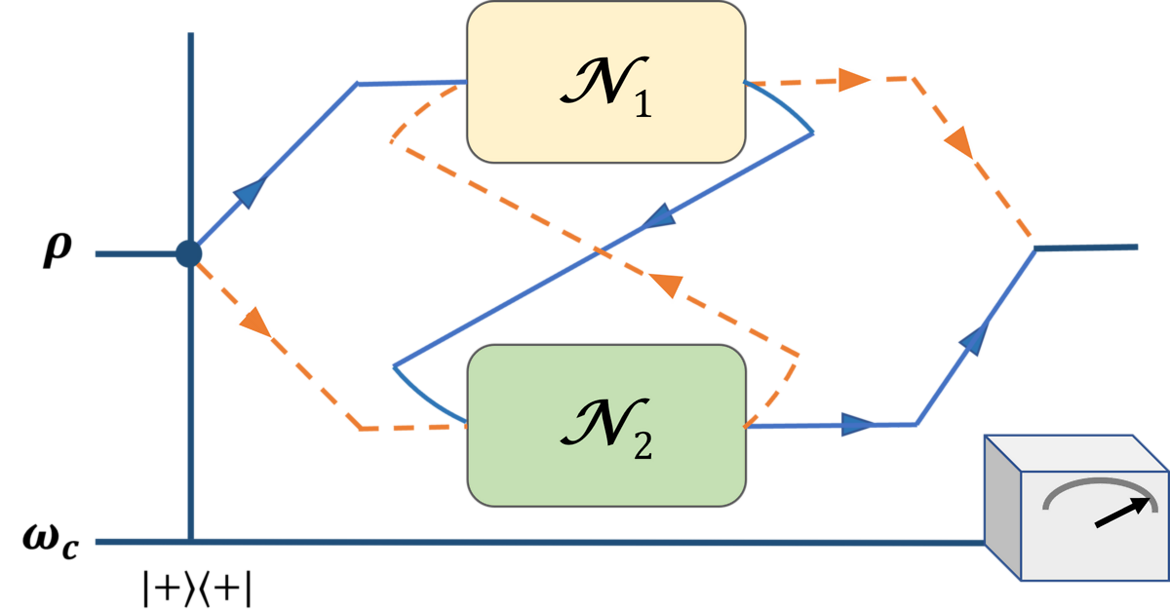
We investigate the dynamical aspects of the quantum switch and find a particular form of quantum memory emerging out of the switch action. We first analyse the loss of information in a general quantum evolution subjected to a quantum switch and propose a measure to quantify the switch-induced memory. We then derive an uncertainty relation between information loss and switch-induced memory. We explicitly consider the example of depolarising dynamics and show how it is affected by the action of a quantum switch. For a more detailed analysis, we consider both the control qubit and the final measurement on the control qubit as noisy and investigate the said uncertainty relation. Further, while deriving the Lindblad-type dynamics for the reduced operation of the switch action, we identify that the switch-induced memory actually leads to the emergence of non-Markovianity. Interestingly, we demonstrate that the emergent non-Markovianity can be explicitly attributed to the switch operation by comparing it with other standard measures of non-Markovianity. Our investigation thus paves the way forward to understanding the quantum switch as an emerging non-Markovian quantum memory.

Estimating the information transmission capability of a quantum channel remains one of the fundamental problems in quantum information processing. In contrast to classical channels, the information-carrying capability of quantum channels is contextual. One of the most significant manifestations of this is the superadditivity of the channel capacity: the capacity of two quantum channels used together can be larger than the sum of the individual capacities. Here, we present a one-parameter family of channels for which as the parameter increases its one-way quantum and private capacities increase while its two-way capacities decrease. We also exhibit a one-parameter family of states with analogous behavior with respect to the one- and two-way distillable entanglement and secret key. Our constructions demonstrate that noise is context dependent in quantum communication.
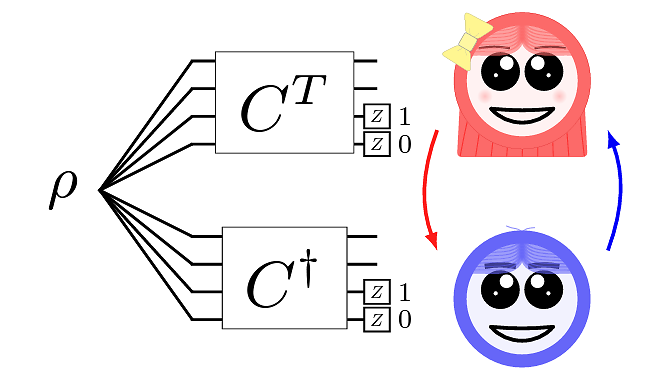
We consider here a set of near-term implementable distillation protocols. These protocols distill n to k pairs by using bilocal Clifford operations, a single round of communication and a possible final local operation depending on the observed measurement outcomes. In the case of permutationally invariant depolarizing noise on the input states, we find a correspondence between these distillation protocols and graph codes. We leverage this correspondence to find provably optimal distillation protocols in this class for several tasks. This correspondence allows us to investigate use cases for so-called non-trivial measurement syndromes. Furthermore, we detail a recipe to construct the circuit used for the distillation protocol given a graph code. We use this to find circuits of short depth and small number of two-qubit gates. We find that these found circuits perform comparable with circuits found based on black-box circuit optimization algorithms. Finally, we investigate the teleportation of encoded states and find protocols which jointly improve the rate and fidelities with respect to prior art.
2024

There are certain dynamics while being non-Markovian, do never exhibit information backflow. We show that if two such dynamical maps are considered in a scenario where the order of application of these two dynamical maps are not definite, the effective channel can manifest information backflow. In particular, we use quantum SWITCH to activate such a channel. In contrast, activation of those channels are not possible even if one uses many copies of such channels in series or in parallel action. We then investigate the dynamics behind the quantum SWITCH experiment and find out that after the action of quantum SWITCH both the CP (Complete Positive)- divisiblity and P (Positive)- divisibility of the channel breaks down, along with the activation of information backflow. Our study elucidate the advantage of quantum SWITCH by investigating its dynamical behavior.
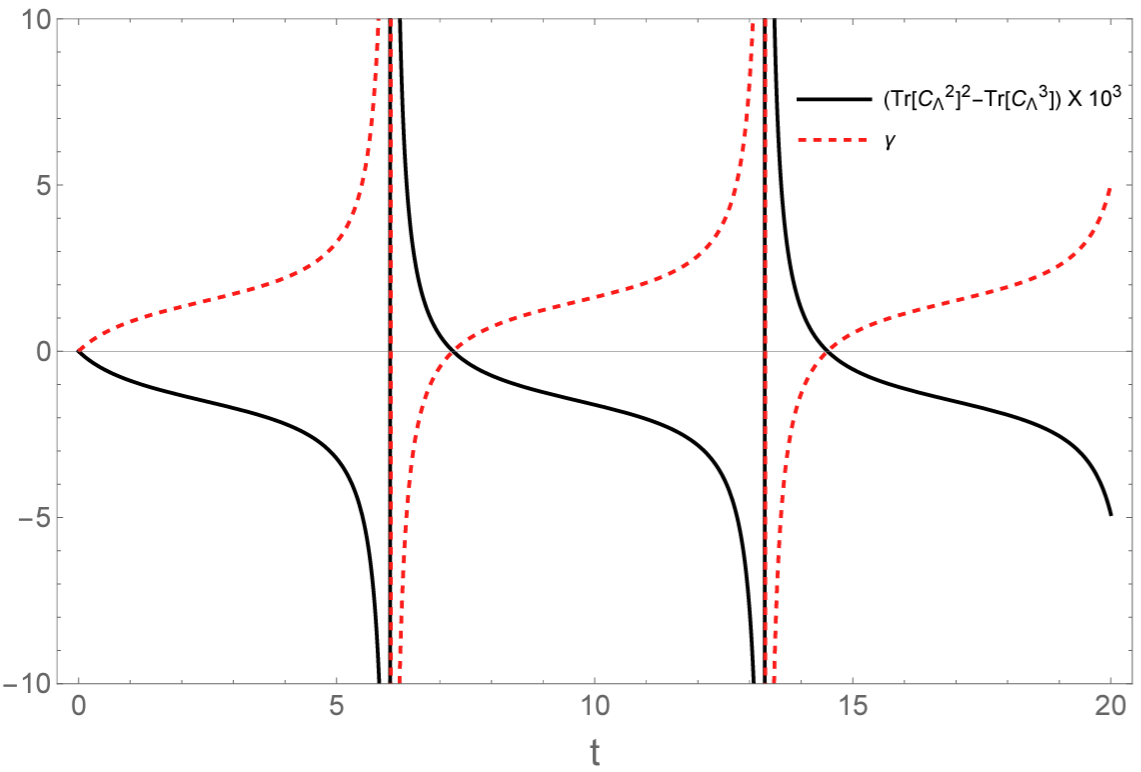
Non-Markovian effects in open quantum system dynamics usually manifest the backflow of information from the environment to the system, indicating complete-positive divisibility breaking of the dynamics. We provide a criterion for witnessing such non-Markovian dynamics exhibiting information backflow, based on partial moments of Choi matrices. The moment condition determined by the positive semi-definiteness of a matrix does not hold for a Choi state describing non-Markovian dynamics. We then present some explicit examples in support of our proposed non-Markovianity detection scheme. Finally, a moment-based measure of non-Markovianity for unital dynamics is formulated.
2023
The quantum internet is the holy grail of quantum information processing, enabling the deployment of a broad range of quantum technologies and protocols on a global scale. However, numerous challenges exist before the quantum internet can become a reality. Perhaps the most crucial of these is the realization of a quantum repeater, an essential component in the long-distance transmission of quantum information. As the analog of a classical repeater, extender, or booster, the quantum repeater works to overcome loss and noise in the quantum channels comprising a quantum network. Here, we review the conceptual frameworks and architectures for quantum repeaters, as well as the experimental progress towards their realization. We also discuss the various near-term proposals to overcome the limits to the communication rates set by point-to-point quantum communication. Finally, we overview how quantum repeaters t within the broader challenge of designing and implementing a quantum internet.
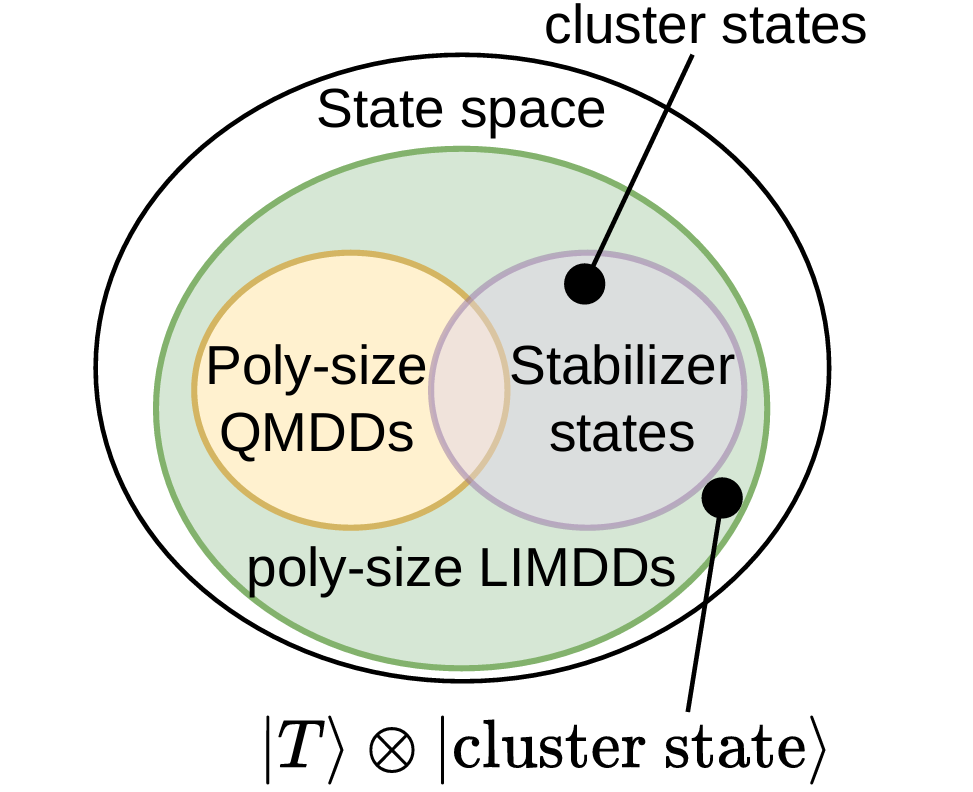
Efficient methods for the representation and simulation of quantum states and quantum operations are crucial for the optimization of quantum circuits. Decision diagrams (DDs), a well-studied data structure originally used to represent Boolean functions, have proven capable of capturing relevant aspects of quantum systems, but their limits are not well understood. In this work, we investigate and bridge the gap between existing DD-based structures and the stabilizer formalism, an important tool for simulating quantum circuits in the tractable regime. We first show that although DDs were suggested to succinctly represent important quantum states, they actually require exponential space for certain stabilizer states. To remedy this, we introduce a more powerful decision diagram variant, called Local Invertible Map-DD (LIMDD). We prove that the set of quantum states represented by poly-sized LIMDDs strictly contains the union of stabilizer states and other decision diagram variants. Finally, there exist circuits which LIMDDs can efficiently simulate, but which cannot be efficiently simulated by two state-of-the-art simulation paradigms: the Clifford + T simulator and Matrix-Product States. By uniting two successful approaches, LIMDDs thus pave the way for fundamentally more powerful solutions for simulation and analysis of quantum computing.
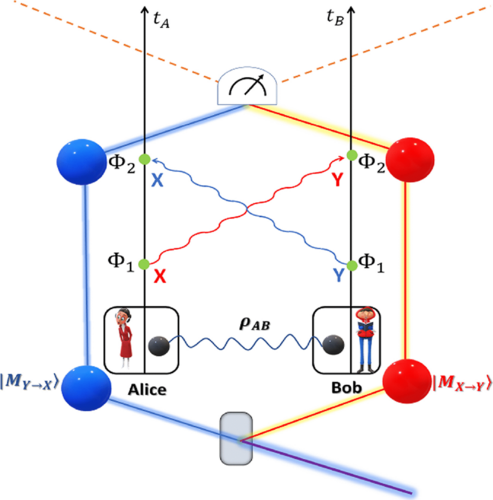
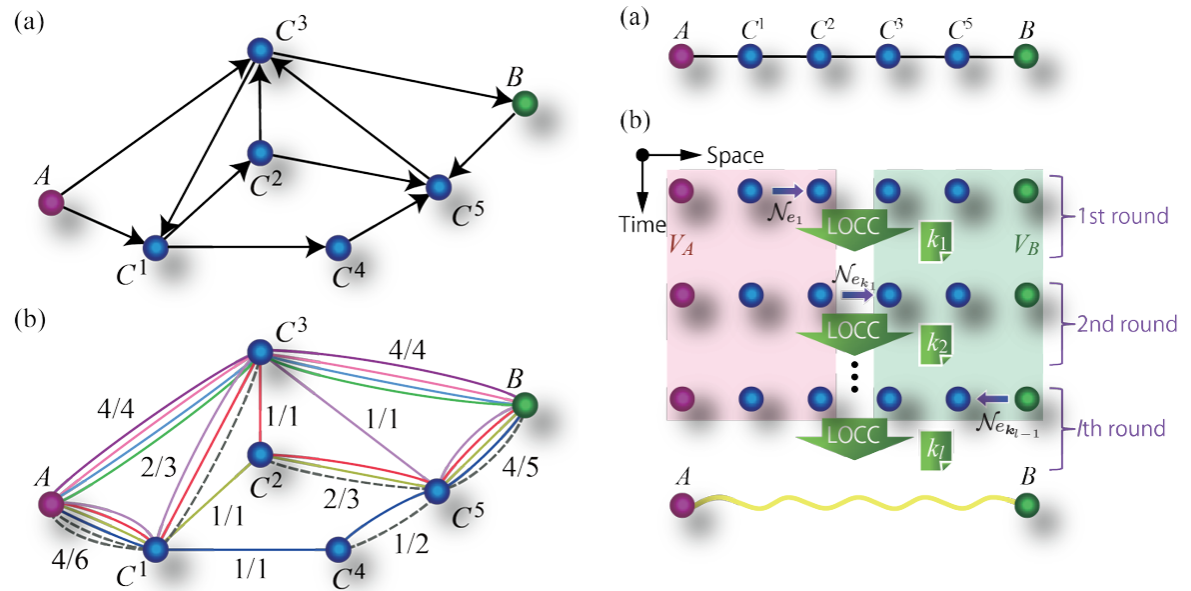
Spatial separation restricts the set of locally implementable quantum operations on distributed multipartite quantum systems. We propose that indefinite causal structure arising due to quantum superposition of different space-time geometries can be used as an independent universal resource for local implementation of any quantum operation on spatially distributed quantum systems. Consequently, all such quantum tasks that are not accomplishable by local operations and classical communication (LOCC) only also become locally accomplishable. We show that exploiting indefinite causal structure as the sole resource, it is possible to perfectly teleport the state of one agent's subsystem to the other distant laboratory in such a way that the agent at the distant laboratory can have access to the whole initially shared state in his or her laboratory and can perform any global quantum operation on the joint state locally. We further find that, after the teleportation process, the resource—indefinite causal structure of the space-time does not get consumed. Hence, after implementing the desired quantum operation the state of the first agent's subsystem can be teleported back to its previous laboratory using the same resource. We show that this two-way teleportation is not always necessary for locally executing all nonlocal quantum tasks that are not realizable by LOCC only. Without invoking any kind of teleportation, we present a protocol for perfect local discrimination of the set of four Bell states that exploits indefinite causal structure as the sole resource. As immediate upshots, we present some more examples of such nonlocal tasks as local discrimination of the set of states exhibiting “quantum nonlocality without entanglement” and activation of bound entangled states that are also achievable by our proposed protocol incorporating indefinite causal structure as a resource.
Estimating noise processes is an essential step for practical quantum information processing. Standard estimation tools require consuming valuable quantum resources. Here we ask the question of whether the noise affecting entangled states can be learned solely from the measurement statistics obtained during a distillation protocol. As a first step, we consider states of the Werner form and find that the Werner parameter can be estimated efficiently from the measurement statistics of an idealized distillation protocol. Our proposed estimation method can find application in scenarios where distillation is an unavoidable step.
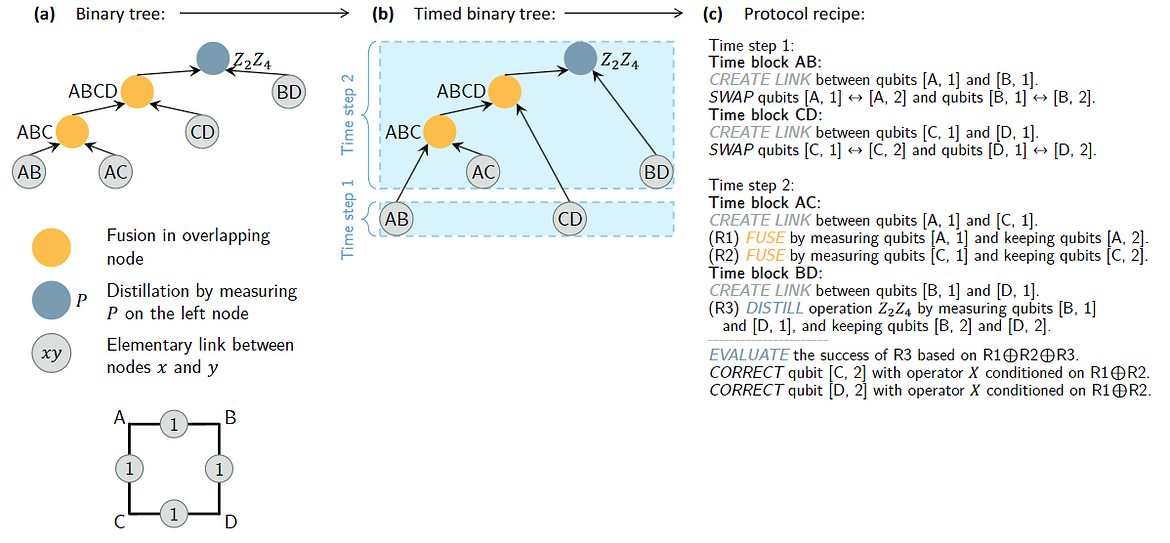
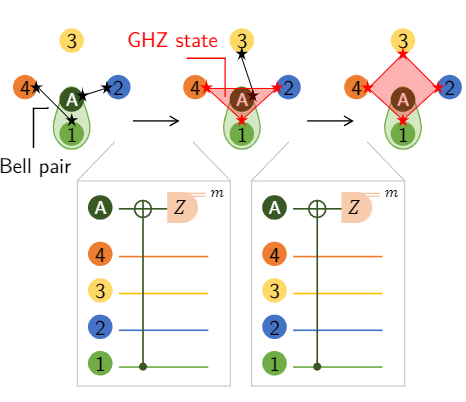
In this paper, we introduce a novel heuristic approach designed to optimize the performance of Greenberger-Horne-Zeilinger (GHZ) creation and distillation protocols under decoherence. Our methodology converts these protocols into a practical set of instructions, demonstrating, through simulations, the production of higher-quality GHZ states than previously known protocols. This advancement contributes to the field of distributed quantum computing by addressing the need for high-quality entanglement required for operations between different quantum computers.

Flag-style fault-tolerance has become a linchpin in the realization of small fault-tolerant quantum-error correction experiments. The flag protocol's utility hinges on low qubit overhead, which is typically much smaller than in other approaches. However, as in most fault-tolerance protocols, the advantages of flag-style error correction come with a tradeoff: fault tolerance can be guaranteed, but such protocols involve high-depth circuits, due to the need for repeated stabilizer measurements. Here, we demonstrate that a dynamic choice of stabilizer measurements, based on past syndromes, and the utilization of elements from the full stabilizer group, leads to flag protocols with lower-depth syndrome-extraction circuits for the [[5,1,3]] code, as well as for the Steane code when compared to the standard methods in flag fault tolerance. We methodically prove that our new protocols yield fault-tolerant lookup tables, and demonstrate them with a pseudothreshold simulation, showcasing large improvements for all protocols when compared to previously-established methods. This work opens the dialogue on exploiting the properties of the full stabilizer group for reducing circuit overhead in fault-tolerant quantum-error correction.
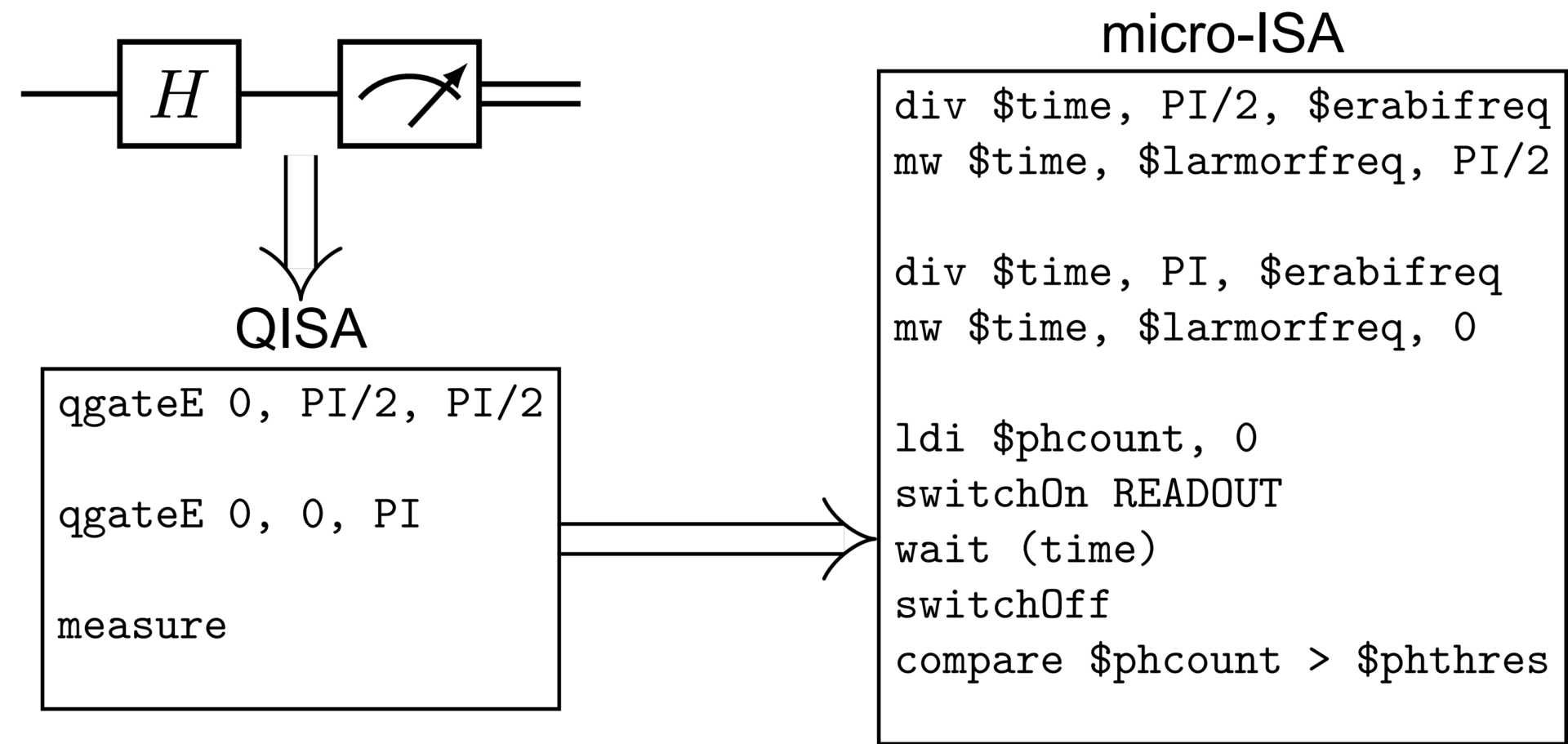
In the world of quantum computing, developments of electronics needed to control (a) qubit(s) rapidly follow one another. Consequently, (micro-)architectures need to be defined to ultimately build control logic. In this paper, we present the (micro-)architecture of a quantum computer based on nitrogen-vacancy (NV) centers in diamonds and a comprehensive simulator capable of mimicking all related (electronic) components as well as quantum operations. We demonstrate that, using our simulator (utilizing noiseless models), we can correctly emulate past (physical) experiments carried out prior to the definition of our architecture.
2022

Quantum networks can enable quantum communication and modular quantum computation. A powerful approach is to use multi-qubit nodes that provide quantum memory and computational power. Nuclear spins associated with defects in diamond are promising qubits for this role. However, dephasing during optical entanglement distribution hinders scaling to larger systems. Here, we show that a 13C-spin quantum memory in isotopically engineered diamond is robust to the optical link operation of a nitrogen-vacancy centre. The memory lifetime is improved by two orders-of-magnitude upon the state-of-the-art, surpassing reported times for entanglement distribution. Additionally, we demonstrate that the nuclear-spin state can survive ionisation and recapture of the nitrogen-vacancy electron. Finally, we use simulations to show that combining this memory with previously demonstrated entanglement links and gates can enable key network primitives, such as deterministic non-local two-qubit gates, paving the way for test-bed quantum networks capable of investigating complex algorithms and error correction.
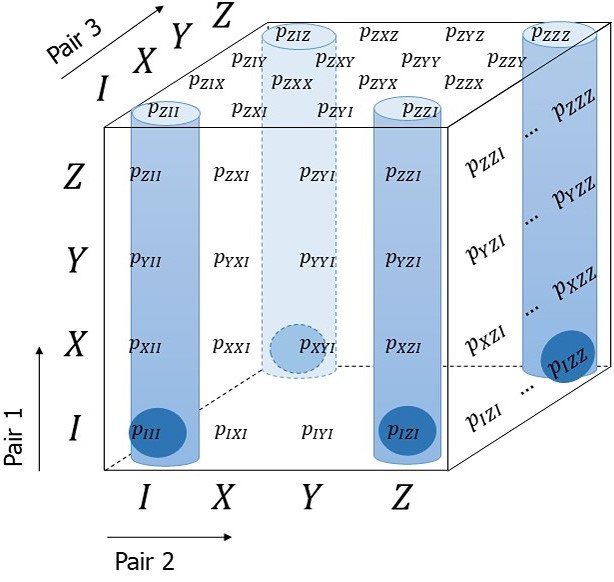
Entanglement distillation is an essential building block in quantum communication protocols. Here, we study the class of near-term implementable distillation protocols that use bilocal Clifford operations followed by a single round of communication. We introduce tools to enumerate and optimise over all protocols for up to n=5 (not necessarily equal) Bell-diagonal states using a commodity desktop computer. Furthermore, by exploiting the symmetries of the input states, we find all protocols for up to n=8 copies of a Werner state. For the latter case, we present circuits that achieve the highest fidelity with perfect operations and no decoherence. These circuits have modest depth and number of two-qubit gates. Our results are based on a correspondence between distillation protocols and double cosets of the symplectic group, and improve on previously known protocols.
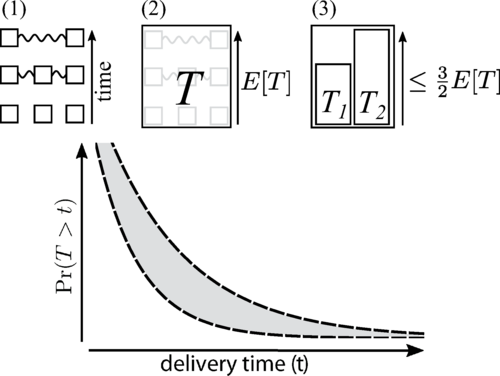
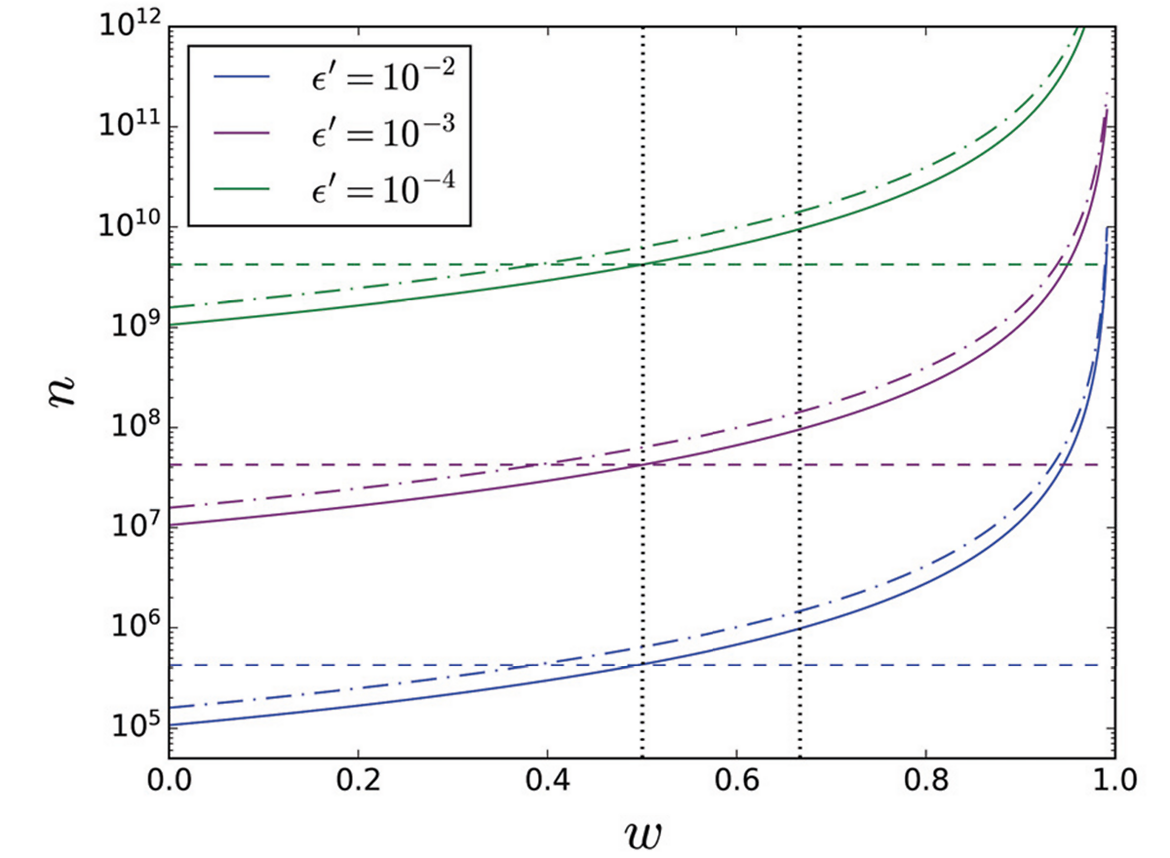
The ability to distribute high-quality entanglement between remote parties is a necessary primitive for many quantum communication applications. A large range of schemes for realizing the long-distance delivery of remote entanglement has been proposed, for both bipartite and multipartite entanglement. For assessing the viability of these schemes, knowledge of the time at which entanglement is delivered is crucial. Specifically, if the communication task requires multiple remote-entangled quantum states and these states are generated at different times by the scheme, the earlier states will need to wait and thus their quality will decrease while being stored in an (imperfect) memory. For the remote-entanglement delivery schemes which are closest to experimental reach, this time assessment is challenging, as they consist of nondeterministic components such as probabilistic entanglement swaps. For many such protocols even the average time at which entanglement can be distributed is not known exactly, in particular when they consist of feedback loops and forced restarts. In this work, we provide improved analytical bounds on the average and on the quantiles of the completion time of entanglement distribution protocols in the case that all network components have success probabilities lower bounded by a constant. A canonical example of such a protocol is a nested quantum repeater scheme which consists of heralded entanglement generation and entanglement swaps. For this scheme specifically, our results imply that a common approximation to the mean entanglement distribution time, the 3-over-2 formula, is in essence an upper bound to the real time. Our results rely on a novel connection with reliability theory.