FY2018 Annual Report
Theory of Quantum Matter Unit
Professor Nic Shannon

Abstract
FY2018 was, once again, a busy year for OIST's Theory of Quantum Matter (TQM) Unit. The Unit was pleased to welcome a new Postdoc, Dr Matthias Gohlke, and was sorry to bid farewell to both Ms Christina Lee, and Dr Rico Pohle, who moved on to a postdoc at the University of Tokyo. Soshi Mizutani, Kim Remund and Andreas Thomasen all successfully defended their Thesis Proposals, and continued to work towards a PhD. Meanwhile, in October 2018, Prof. Shannon began his Sabbatical, as August Wilhelm Scherrer Visting Professor at the Technical University of Munich, hosted in the group of Prof. Frank Pollmann.
The Unit published 8 papers in FY 2018, including one article in Nature Physics, two in Physical Review Letters, and one in Physical Review B Rapid Communications, which was also singled out as an Editor's Selection. These covered a range of topics in the physics of quantum materials, and topological phases of matter. Research highlights included new insights into quantum spin liquids; the explanation of the "half-moon" features observed in neutron scattering from many frustrated magnets; the discovery of a connection between "fractons" in a curved space and holography; the explanation of negative thermal expansion in Cr spinels; and work on the optical manipulation of magnetic domains, which could contribute to future data storage technologies.
The Unit remained active in promoting its work, giving a total of 39 presentations in FY2018, including 24 invited talks. Significantly, the work of Unit Members was presented in three different invited talks at the March Meeting of the American Physical Society; in both invited and contributed talks at the International Conference on Magnetism (ICM 2018); and in both invited and contributed talks at the conference Highly Frustrated Magnetism (HFM 2018). Other venues included international workshops in Dresden, Hsinchu, Kyoto and Pohang, and seminars or colloquia at institutions including Ecole Normale Superior, John Hopkins University, Ludwig Maximillian University, Stanford, and the University of Tokyo.
The Unit hosted a total of 20 visitors in FY2018, who between them gave 18 research seminars, as well as a lecture course on "Field-theory approach to quantum many-body systems". And it also continued its tradition of outreach activity, with Dr Tokuro Shimokawa addressing students in Hyogo interested in the possibility of a career in Research.
1. Staff
- Dr. Judit Romhanyi, Staff Scientist
- Dr. Matthias Gohlke, Postdoctoral Scholar
- Dr. Geet Rakala, Postdoctoral Scholar
- Dr. Tokuro Shimokawa, Postdoctoral Scholar
- Mr. Soshi Mizutani, PhD Student
- Ms. Kimberly Remund, PhD Student
- Mr. Andreas Thomasen, PhD Student
- Mr. Han Yan, PhD Student
- Ms. Christina Lee, Student
- Ms. Megumi Ikeda, Research Unit Administrator
2. Collaborations
2.1 Multiple-q state in the classical frustrated honeycomb-lattice antiferromagnet under magnetic field
- Type of collaboration: Joint research
- Researchers:
- Dr. Tokuro Shimokawa, OIST
- Dr. Tsuyoshi Okubo, University of Tokyo
- Prof. Hikaru Kawamura, Osaka University
2.2 High-field magnetism of the quantum honeycomb-lattice antiferromagnet
- Type of collaboration: Joint research
- Researchers:
- Dr. Tokuro Shimokawa, OIST
- Mr. Akira Okutani, Osaka University
- Dr. Takanori Kida, Osaka University
- Prof. Yasuo Narumi, Osaka University
- Prof. Zentaro Honda, Saitama University
- Prof. Koichi Kindo, University of Tokyo, ISSP
- Prof. Takehito Nakano, Ibaraki University
- Prof. Yasuo Nozue, Osaka University
- Prof. Masayuki Hagiwara, Osaka University
2.3 Thermal and quantum fluctuation effects to the S=1/2 bilayer breathing-kagome magnet
- Type of collaboration: Joint research
- Researchers:
- Dr. Tokuro Shimokawa, OIST
- Prof. Nic Shannon, OIST
2.4 Rank–2 U(1) spin liquid on the breathing pyrochlore lattice
- Type of collaboration: Joint research
- Researchers:
- Mr. Han Yan, OIST
- Prof. Nic Shannon, OIST
- Dr. Owen Benton, RIKEN Center for Emergent Matter Science (CEMS)
- Dr. Ludovic D.C. Jaubert, CNRS, Universit ́e de Bordeaux, LOMA
2.5 Topological excitations in quantum magnets
- Type of collaboration: Joint research
- Researchers:
- Dr. Judit Romhanyi, OIST
- Prof. Karlo Penc, Wigner Research Centre for Physics
2.6 Magnetoelectric multiferroics
- Type of collaboration: Joint research
- Researchers:
- Dr. Judit Romhanyi, OIST
- Dr. Mitsuru Akaki, Osaka University
- Dr. Sándor Bordács, Budapest University of Technology and Economics and MTA-BME Lendület Magneto-optical Spectroscopy Research Group
- Dr. Vilmos Kocsis, RIKEN Center for Emergent Matter Science (CEMS)
- Prof. Karlo Penc, Wigner Research Centre for Physics
- Prof. István Kézsmárki, Center for Electronic Correlations and Magnetism, University of Augsburg
- Prof. Yoshinori Tokura, RIKEN Center for Emergent Matter Science (CEMS), University of Tokyo,
- Prof. Masayuki Hagiwara, Osaka University
2.7 Topological states in the Kronig-Penney model
- Type of collaboration: Joint research
- Researchers:
- Ms. Irina Reshodko, OIST
- Dr. Albert Benseny, OIST
- Dr. Judit Romhanyi, OIST
- Prof. Thomas Busch, OIST
2.8 Polarization plateaus in hexagonal water ice
- Type of collaboration: Joint research
- Researchers:
- Dr. Matthias Gohlke, OIST
- Prof. Roderich Moessner, MPI-PKS
- Prof. Frank Pollmann, TUM
2.9 Topological excitations in Kitaev-like frustrated magnets
- Type of collaboration: Joint research
- Researchers:
- Dr. Matthias Gohlke, OIST
- Dr. Jeff Rau, MPI-PKS
- Dr. Paul McClarty, MPI-PKS
- Prof. Roderich Moessner, MPI-PKS
- Prof. Karlo Penc, Wigner Research Centre for Physics
2.10 Z6 parafermions on the triangular lattice Ising antiferromagnet with further neighbor interactions
- Type of collaboration: Joint research
- Researchers:
- Dr. Geet Rakala, OIST
- Prof. Kedar Damle, TIFR
2.11 Hard plates on the cubic lattice
- Type of collaboration: Joint research
- Researchers:
- Dr. Geet Rakala, OIST
- Prof. Kedar Damle, TIFR
- Mr. Dipanjan Mandal, IMSc
- Prof. R Rajesh, IMSc
- Prof. Deepak Dhar, IISER
2.12 Machine learning the relaxation of a density wave in cold atom system
- Type of collaboration: Joint research
- Researchers:
- Mr. Soshi Mizutani, OIST
- Prof. Nic Shannon, OIST
- Mr. Tobias Schnurrenberger, Ludwig Maximilian University of Munich (LMU)
- Prof. Ulrich Schollwöck, LMU
2.13 Application of machine learning to numerical calculations of dynamical spin structure factors
- Type of collaboration: Joint research
- Researchers:
- Mr. Soshi Mizutani, OIST
- Prof. Nic Shannon, OIST
- Prof. Frank Pollmann, Technical University of Munich (TUM)
- Prof. Jean-Sébastien Caux, Institute for Theoretical Physics (ITFA), University of Amsterdam
2.14 Negative Thermal Expanstion in Cr spinels
- Type of collaboration: Joint research
- Researchers:
- Prof. Nic Shannon, OIST
- Dr. Lisa Rossi, HFML-EMFL, Radboud University
- A. Bobel, HFML-EMFL, Radboud University
- Dr. Steffen Wiedmann, HFML-EMFL, Radboud University
- Dr. Robert Kuchler, Max Planck Institute for Chemical Physics of Solids
- Prof.Yukitoshi Motome, The University of Tokyo
- Prof. Karlo Penc, Wigner Research Centre for Physics
- Prof. Hiroaki Ueda, Kyoto University
- Dr. Ben Bryant, HFML-EMFL, Radboud University
3. Activities and Findings
3-1. Electromagnetism beyond Maxwell’s Equations
Condensed Matter is a beautiful playground for low-energy realisation of high-energy phenomena. This is especially true in strongly correlated magnetism, where spin-spin correlations can be described as effective gauge fields. Quantum spin ice is a canonical example of this physics, supporting an emergent electromagnetic gauge field. Searching for photon and magnetic monopoles in these systems is an exciting venue, but over the past years, a growing question has been stimulating the community: is it possible to go beyond electromagnetism ?
To join this quest, the approach of the TQM Unit has been to seek the realisation of higher-rank gauge fields, in collaboration with Dr. Owen Benton (RIKEN) and Dr. Ludovic Jaubert (CNRS, Univ. Bordeaux). Where electromagnetism is of rank 1, described by vector fields and scalar charges, higher-rank gauge fields require a higher dimension of description; e.g. the fields are tensors and the charges are, counter-intuitively, vectors ! As is often the case in physics, going to higher dimensions offer a plethora of new opportunities, but every rose has its thorn. To go from vector to tensor gauge fields, substantially more complex spin-spin correlations are needed. Finding a model stabilising such correlations is a challenge by itself, which is why most attempts so far have led to largely artificial Hamiltonians, away from materials.
The breakthrough of the TQM Unit has been to propose a realistic microscopic model supporting such rank-2 gauge field, on the breathing pyrochlore lattice made of alternating small and large tetrahedra. This proposal is based on a classical field theory, supported by Monte Carlo simulations, and shows the typical four-fold pinch point of a rank-2 gauge field, as would be observed in polarised neutron scattering experiments (cf. Fig.). The model is simply a Heisenberg antiferromagnet with Dzyaloshinskii–Moriya perturbations on the small tetrahedra. Such Hamiltonian is strongly reminiscent of the parametrisation of the Ba3Yb2Zn5O11 breathing pyrochlore, suggesting that future experimental realisations are only one step away!
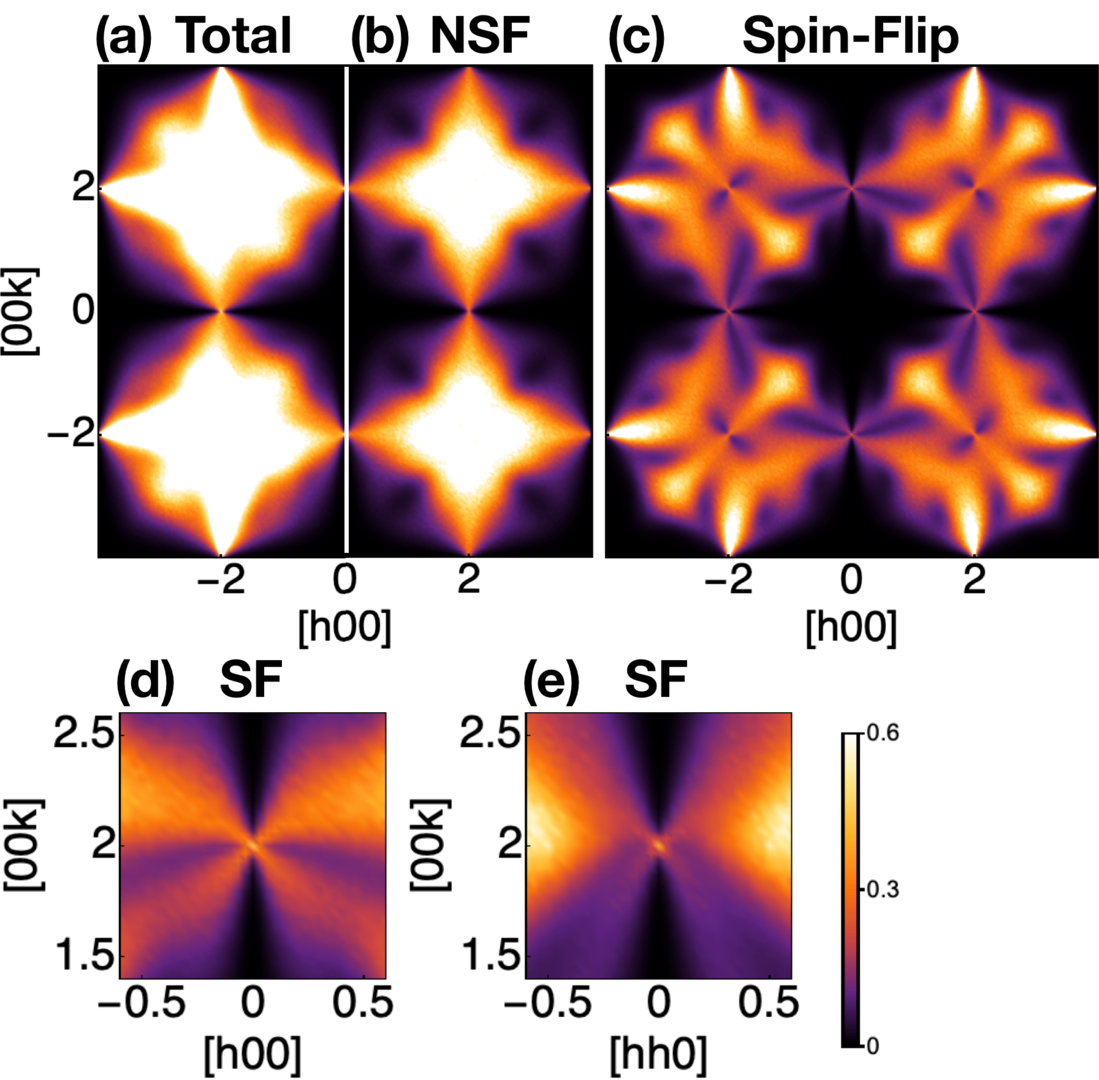
Structure factor of our rank-2 gauge field on the breathing pyrochlore lattice, as would be measured by polarised neutron scattering, in the [h0k] plane: (a) total scattering, (b) non-spin flip channel, (c) spin flip channel with the four-fold pinch points, zoomed in panel (d). Panel (e) displays the four-fold pinch point in the [hhk] plane.
This work was published as Han Yan, Owen Benton, Ludovic D.C. Jaubert and Nic Shannon, "Rank–2 U(1)Spin Liquid on the Breathing Pyrochlore Lattice" Phys. Rev. Lett. 124, 127203 (2020).
3-2. Multiple-q states of the J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet under magnetic fields
There is now a growing interest in rich non-trivial magnetic structures known as “multiple-q states” which are coherent superpositions of states with different ordering wavevectors. One of celebrated examples might be the “skyrmion-lattice state” which is often stabilized in the system with antisymmetric Dzyaloshinskii-Moriya (DM) interaction. Motivated by a theoretical study for the emergence of a frustration-induced symmetric skyrmion-lattice state in a triangular-lattice Heisenberg magnet without DM interaction, we investigate the ordering properties of the classical J1-J2 honeycomb-lattice Heisenberg antiferromagnet under magnetic field (Fig. 1) by means of a large-scale monte carlo simulation, a low-temperature expansion and a mean-field analysis. It was reported that the classical ground state of the honeycomb-lattice system has an infinite ring-like degeneracy in the wave vector space (Fig. 2) and this degeneracy could produce exotic cooperative paramagnetic states called by "ring-liquid state" and "pancake-liquid state" at moderate temperatures under zero magnetic field. In our manuscript, we find that the ring-like degeneracy could be a source for a rich variety of multiple-q states including the single-q (umbrella and fan types), double-q (coplanar and non-coplanar types) and triple-q states (collinear type), at moderate temperatures under magnetic fields (Fig. 3). One of the double-q state, double-q (type3), has meron/antimeron-like spin textures. We also discuss the possible origin of the various multiple-q states observed in our MC simulations within a mean-field analysis and a low-temperature expansion method.
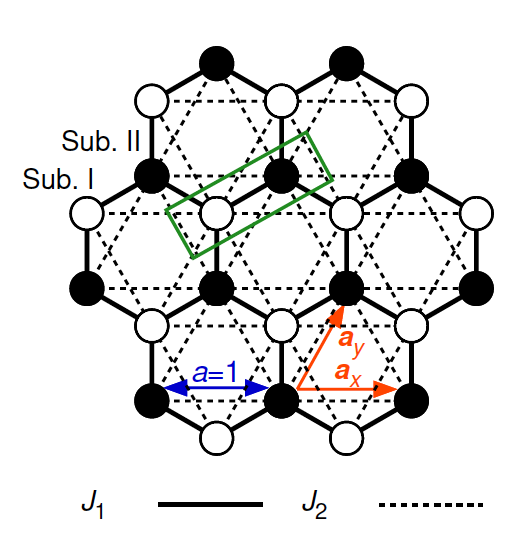
J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet
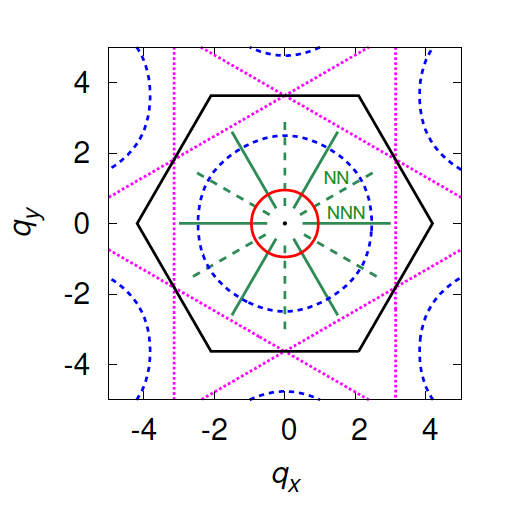
Ground-state degeneracy curves in reciprocal space for J2/J1=0.18 (red), 0.30(blue) and 0.50(purple), respectively
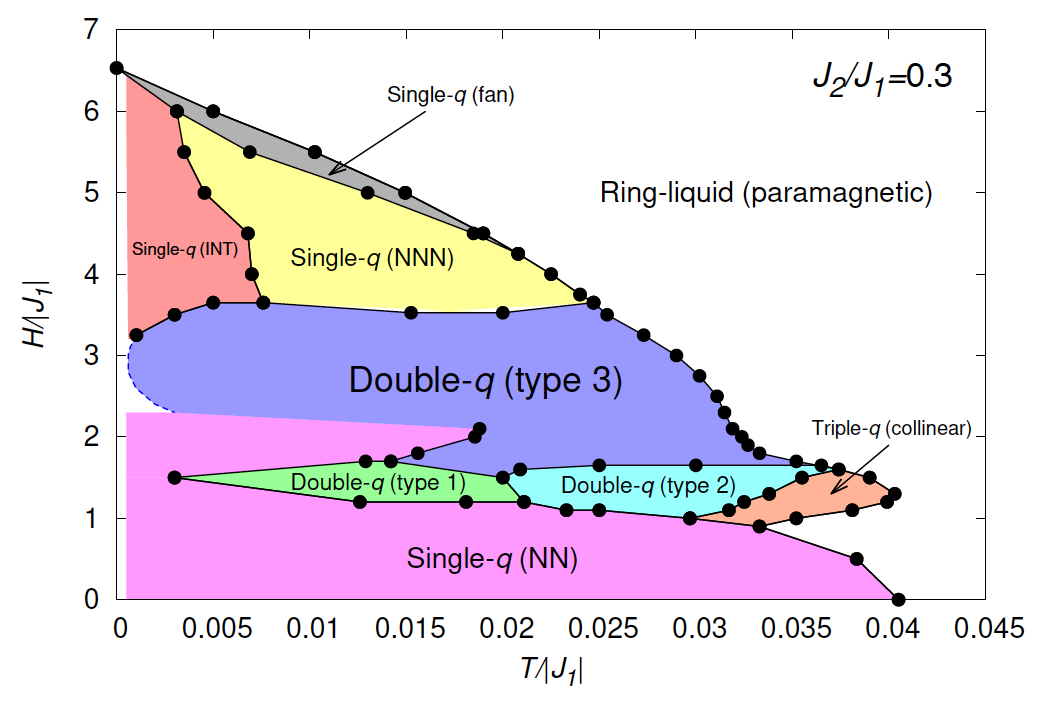
Finite-temperature phase diagram under magnetic field for J2/J1=0.30
This work was published as Tokuro Shimokawa, Tsuyoshi Okubo and Hikaru Kawamura "Multiple-q states of the J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet under magnetic fields" Phys. Rev. B 100, 224404 (2019).
3-3. Topological states in the Kronig–Penney model with arbitrary scattering potentials
The Kronig–Penney (KP) model is one of the fundamental models, taught in almost every solid state classes. Despite its simplicity, it is particularly well suited to describe the behavior of electrons in metals. Assuming potentials at non-periodic positions or having random strengths, the KP model can describe impurities or disorder in a straightforward manner.
In this work, we use the coordinate Bethe ansatz approach for such arbitrary KP model in finite geometry and demonstrate the appearance of topological edge states.
A nontrivial topology is marked by a nonzero topological invariant, such as the first Chern number in the case of two dimensional systems. To have a second periodic parameter that can be considered as a virtual dimension, we apply a shift Δ to the scatterers with respect to the wall of the box. According to the bulk-boundary correspondence, the number of edge modes in the gap has to be related to the sum of the Chern numbers of the bands up to the given gap. In the first gap, we have one edge mode with positive and one negative velocity, located on the opposite ends and corresponding to c1 = 1. In the second gap, the number of edge modes becomes two for both sides, reflecting a total Chern number c2 = 2, and so on.
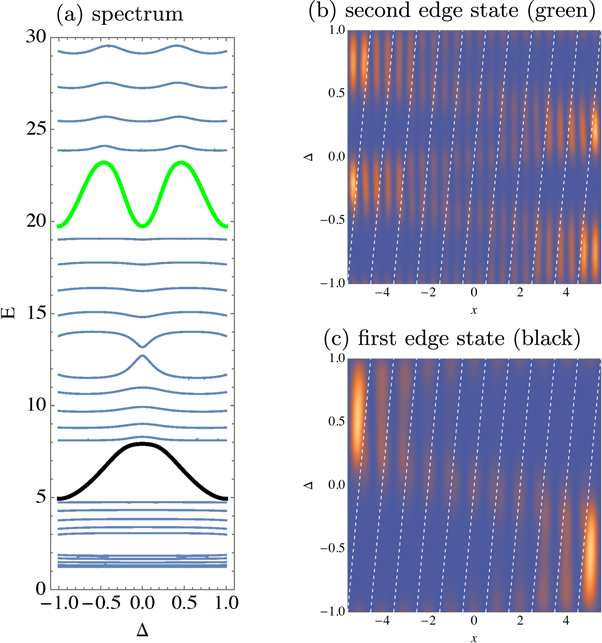
(a) Spectrum of the KP model with equidistant scatterers of alternating heights as a function of the Δ shift. Each band has a Chern number 1. The green and black line denote the in-gap edge modes. (b) and (c) illustrate the density distribution of the edge states across the box. For Δ =-1,0 and 1, the modes are extended and melt into the bulk. For other values, they are localized at the sides of the box.
This work was published as Irina Reshodko, Albert Benseny, Judit Romhányi and Thomas Busch "Topological states in the Kronig–Penney model with arbitrary scattering potentials" New J. Phys., 21 013010 (2019)
3-4. When neutrons see stars ... and half moons
Looking inside matter is not a dream, but an every-day achievement in labs around the world. The scattering of neutrons is a powerful, and broadly used, method to probe the microscopic details inside magnets. Magnetic order, or on the opposite the complete absence thereof, can be easily observed by neutrons. But what about more subtle correlations? A growing number of exotic magnets present complicated features in neutron scattering, due to unconventional correlations. These features often need to be analysed case by case, and it is difficult to find generic patterns. Here, we identify and explain a new pair of generic patterns, with the appearance of a “half-moon” and a “star”. They are the natural consequence of the proximity of a Coulomb spin liquid, emerging from the local clustering of magnetic degrees of freedom. In other words, half-moons and stars appear in systems where flat bands of excitations are not ground state anymore. Being the generic signature for a family of models with flat bands, half-moons and stars are now distinctive features to be looking for in neutron scattering.
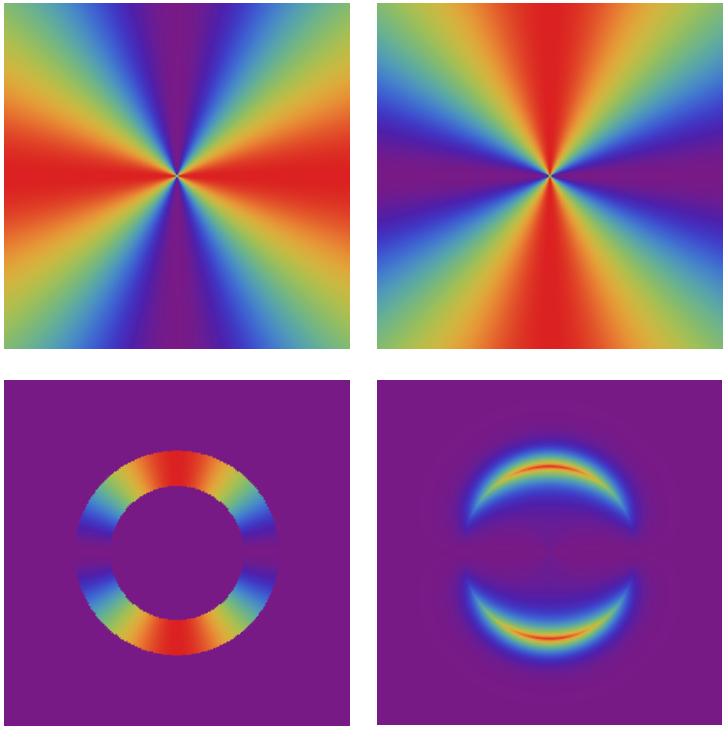
This work was published as Tomonari Mizoguchi, Ludovic D. C. Jaubert, Roderich Moessner, and Masafumi Udagawa "Magnetic clustering, half-moons, and shadow pinch points as signals of a proximate Coulomb phase in frustrated Heisenberg magnets" Phys. Rev. B 98, 144446 (2018)
3-5. Statistical properties of worm algorithms
Worm algorithms have been shown as a very useful means of generating non-local updates in frustrated models of magnetism.
Here we study the statistical properties of two previously developed worm algorithms for triangular and Kagome lattice antiferromagnets with further neighbor interactions. The ‘worm’ construction typically starts by creating a defect and an antidefect next to each other in the initial configuration. The location of the defect defines the fixed tail of the worm, while the head of the worm corresponds to the antidefect, which is moved through the lattice in a way which satisfies detailed balance conditions in a larger configuration space that allows for one defect-antidefect pair. The construction ends when the head reaches the tail again and annihilates it. All variables encountered during the motion of the worm are updated as a result of this construction.
We establish that the statistical properties of the worms depend only on the universal long-distance properties of the underlying equilibrium ensemble, and not on the details of the worm algorithm or microscopic Hamiltonian.
Viewing each step of the worm construction as a position increment (step) of a random walker, we argue that the power-law correlations of the underlying equilibrium system give rise to two related properties of this walk:
First, the walk is conducted in a logarithmic central potential whose strength is set by the power-law exponent of the equilibrium defect-antidefect correlation function. Second, the steps of the walk are correlated. By comparing our measured statistical properties of the worms to expected scaling relations, we establish that the worms define a discrete-time realization of a fractional Brownian motion which has a conventional steady-state given by the equilibrium Gibbs distribution of a particle in a logarithmic central attractive potential.
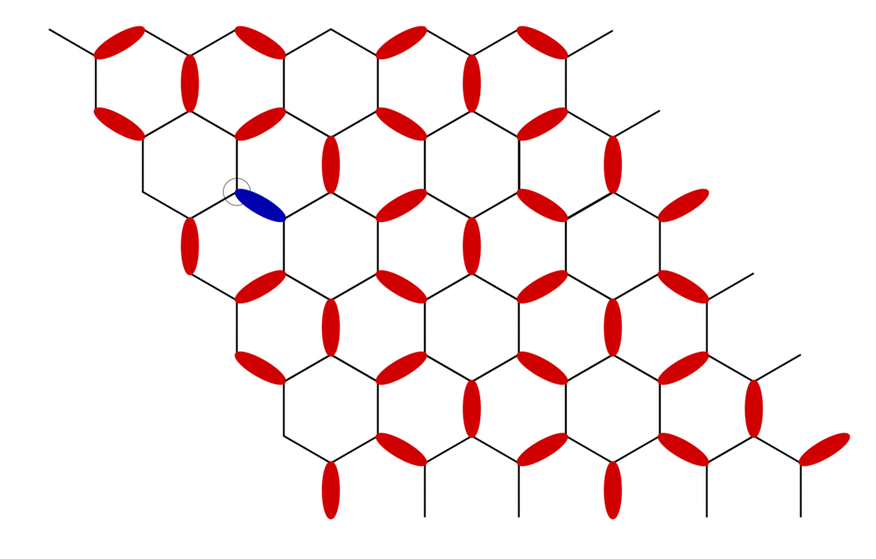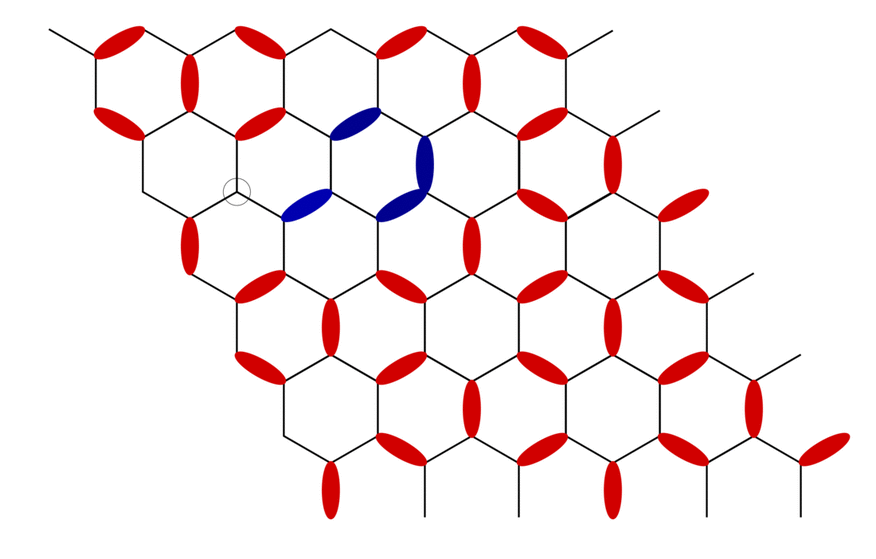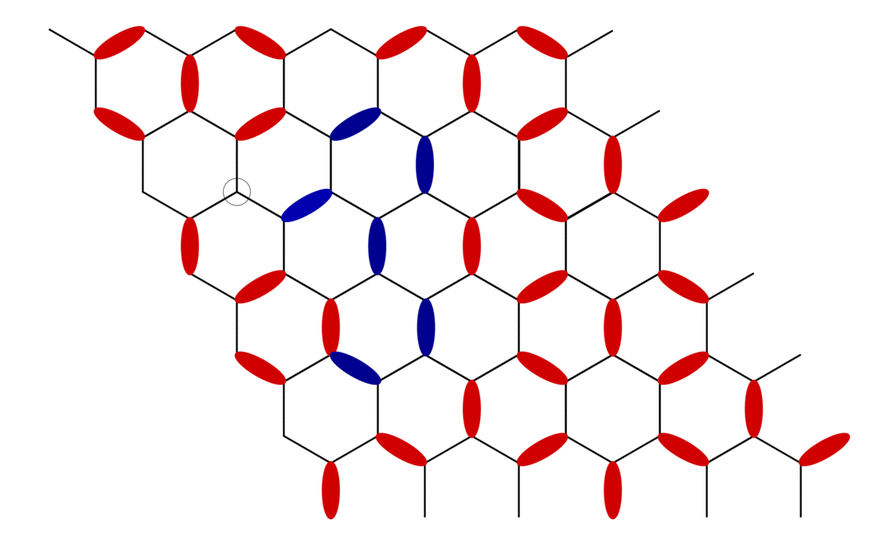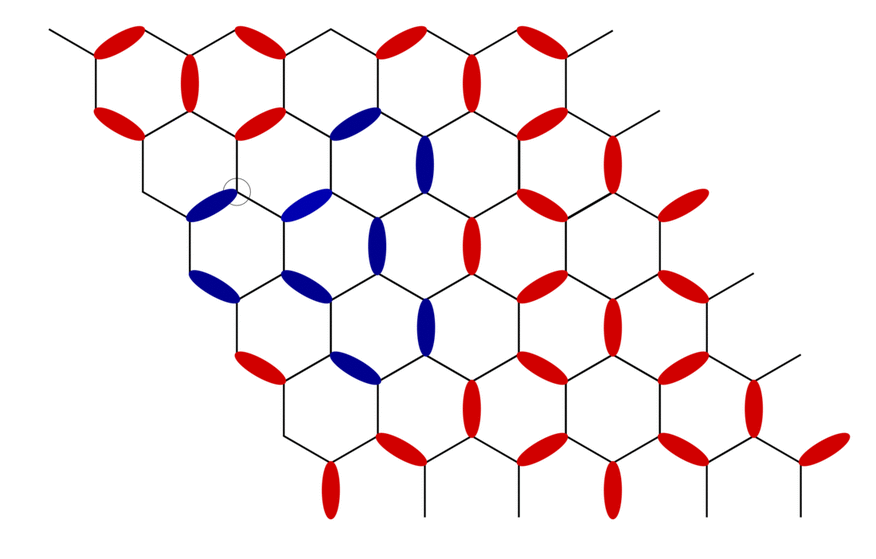
A typical worm propagating through the fully packed dimer model on the honeycomb lattice. A defect here is the lattice site with no dimers touching it and an antidefect is the lattice site with two dimers touching it. The worm ends when the initial defect is annihilated by the propagating antidefect.
This work was published as Geet Rakala, Kedar Damle, and Deepak Dhar, "Fractional Brownian motion of worms in worm algorithms for frustrated Ising magnets" Phys. Rev. E 103, 062101 (2021).
3-6. Demystifying the half moon pattern
Magnetic frustration leads to the emergence of diverse exotic behaviors, and the study of their theories and phenomenology is crucial. For example, sophisticated understanding has been established for models with underlying U(1) symmetry and the associated pinch-point features in their spin-spin correlations.
However, this turned out to be only half the story. Attached to the pinch points, there exists another highly universal feature in the shape of two “half moons” in a wide range of frustrated magnetic models and recent experiments on Nd2Zr2O7.
In this work we establish its theoretical interpretation, which turned out to be a hidden side of the pinch-points. It is a result of decomposition and decoupling of the emergent magnetic field in the system, which leads to an extra pinch point on the dispersive band. The half moons are essentially the pinch points seen on a constant energy cross-section.
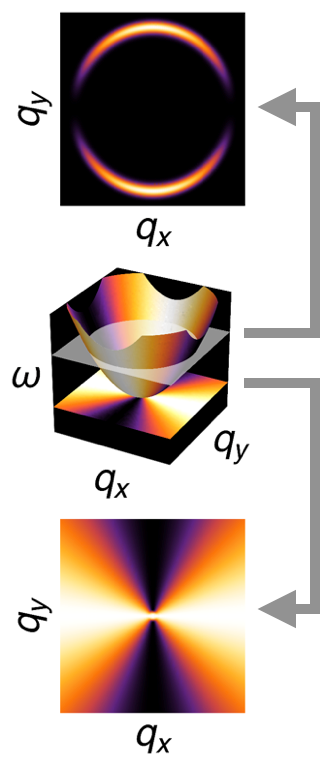
Illustration of connection between pinch points and half moons. Upper panels: flat and dispersing bands of spin excitations, showing cross-sections at fixed energy (white plane). Lower panels: corresponding prediction for the dynamical structure factor at fixed energy. Pinch-point singularities are encoded in both the flat, and the dispersing band, where they appear as half-moon features.
This work was published as Han Yan, Rico Pohle and Nic Shannon, "Half moons are pinch points with dispersion" Phys. Rev. B, 98 140402(R) (2018). It was also singled out as an Editor's Suggestion, and for inclusion in Kalaidascope.
3-7. Fracton and holography
A long term ambition of condensed matter physics is to understand all possible quantum phases of matter. Recently, a new class of so-called “fracton phases” has attracted considerable interest in the communities of condensed matter theory and quantum information. “Fractons” are a type of exotic excitations in the system that cannot be moved by local dynamics. They character new states of matter beyond the conventional Landau symmetry breaking or topological order classification.
In this work, a simple classical fracton model is investigated in the context of holography. Holography is a conjectured principle that in negatively curved spacetime, gravitational theory is equivalent to some conventional quantum field theory on the boundary of the spacetime. We found that some of the most essential properties of holography are realized on the fracton model, including how the boundary is entangled, and how the bulk and boundary correspond to each other. This discovery implies a deeper connection between gravity and fracton phase of matter to be explored.
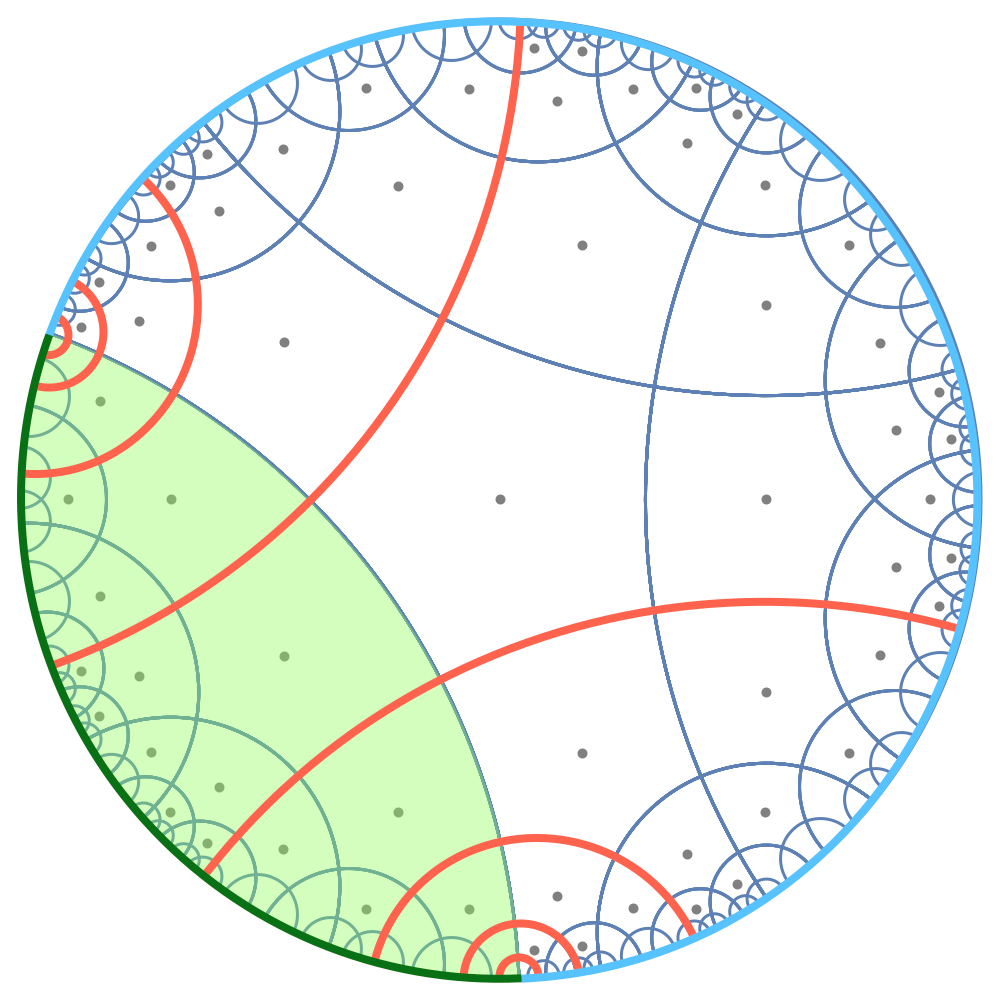
The mutual information of a boundary connected bipartition in the hyperbolic fracton model obeys Ryu-Takayanagi formula, a key property from holography.
These work was published as Han Yan "Hyperbolic fracton model, subsystem symmetry, and holography" Phys. Rev. B 99 155126 (2019). It was singled out as an Editor's Suggestion, and for inclusion in Kalaidascope.
3-8. Ripple state in the frustrated honeycomb-lattice antiferromagnet
Rich non-trivial magnetic structures in "multiple-q states" have attracted much attention these days owing to their novel thermodynamic ordering phenomena and unique transport properties. A celebrated example might be a "skyrmion-lattice state" known as a triple-q state with forming periodic vortex-crystal structures. In this article, we have discovered a new type of multiple-q state, a "ripple state" in the J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet under magnetic field by extensive Monte Carlo simulations. This weird state does not form a crystal in spite of the breaking of the translational symmetry and can be considered as an "infinituple-q" state composed of an infinite number of spiral wavevectors. One of the most impressive features in the ripple state is its real-space spin texture which seems to be like a "water ripple" observed when we throw a stone on water surface (see Fig. 1). The interference effect between ripples is also observed and vortex/antivortex defects are detectable (See Fig. 2). We have found that the ripple state appears with a second-order phase transition via a spiral-spin liquid state, “ring-liquid state”. The possible realization of the ripple state in the honeycomb-lattice spin-liquid material Bi3Mn4O12(NO3) is discussed.
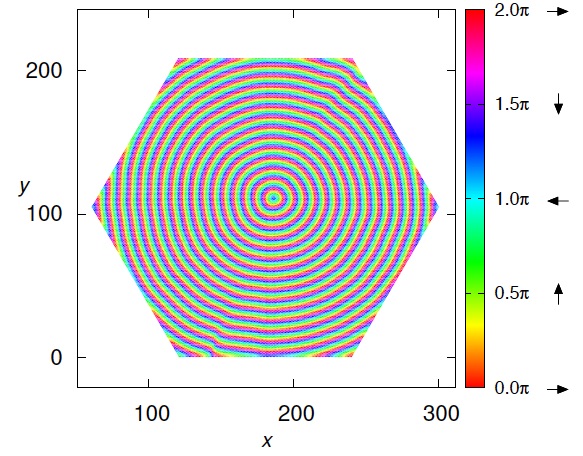
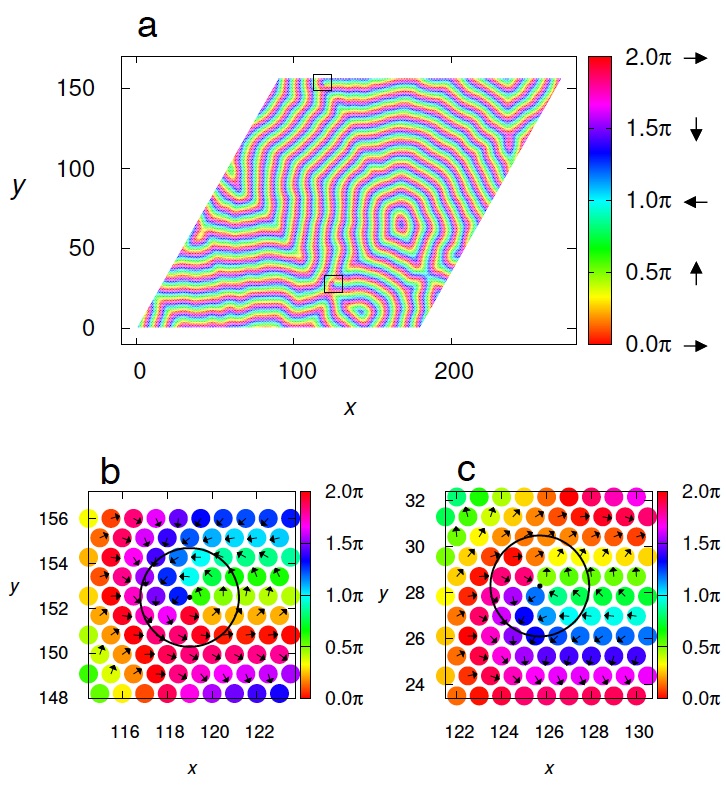
These work was published as Tokuro Shimokawa and Hikaru Kawamura "Ripple state in the frustrated honeycomb-lattice antiferromagnet" Phys. Rev. Lett. 123, 057202 (2019).
3-9. Negative thermal expansion in Cr spinels
Almost every object around us expands when it is heated up, and contracts when it is cooled down. This "thermal expansion" reflects the way in which energy is stored in the atoms which make up the material. In simple terms, the hotter these atoms are, the more they move, and the more bonds between different atoms are "stretched" leading to an overall expansion. Thermal expansion has to taken into account in designing any structure subject to changes in temperature, including buildings, bridges, roads, and moving components in machines.
Materials with negative thermal expansion are of technological interest since they can be used, among other things, to compensate for the positive thermal expansion of components with more conventional properties. However they are also very unusual, and perhaps the only common examples are elastic bands, which contract when heated, and water, which expands when frozen. In both cases, the driving force is the driving force is not energy but entropy, a measure of the number of different ways in which atoms can organise themselves.
In this study, we report the discovery of negative thermal expansion in magnetic spinel material, Cd2CrO4, and present a theoretical explanation for this new phenomenon. Cd2CrO4 is already well-known for its magnetic "frustration", which increases the entropy available at low temperatures, and for its unusual properties in high magnetic field. State-of-the art dilatometry measurements, carried out in the High Field Magnet Laboratory in Nijmegen, Netherlands, revealed that, for a wide range of temperatures and magnetic fields, Cd2CrO4, like water ice, expands as it is cooled. We have developed a microscopic theory for this negative thermal expansion (NTE), building on earlier work on the coupling between magnetic Cr ions and the crystal lattice [Penc and Shannon and Shiba Phys. Rev. Lett 93, 197203 (2004)]. We find that the driving force for NTE comes, once again, from entropy, this time enocded in nearly-localised spin excitations, which are coupled strongly to the lattice. This work offers new insights into both the physics of Cr spinels, and of the possibility of NTE in other frustrated materials.
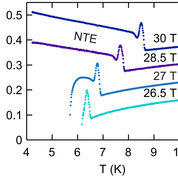
Change in size of a crystal of Cd2CrO4 as a function of the temperature and magnetic field. The sample shows a marked negative thermal expansion (NTE), which originates in the coupling between magnetic atoms and the crystal lattice.
These results were published as L. Rossi, A. Bobel, S. Wiedmann, R. Küchler, Y. Motome, K. Penc, N. Shannon, H. Ueda and B. Bryant: "Negative Thermal Expansion in the Plateau State of a Magnetically Frustrated Spinel" Phys. Rev. Lett. 123, 027205 (2019).
4. Publications
4.1 Journals
- Judit Romhányi, Multipolar edge states in the anisotropic kagome antiferromagnet, doi: 10.1103/PhysRevB.99.014408 (2018).
- Irina Reshodko, Albert Benseny, Judit Romhányi and Thomas Busch, Topological states in the Kronig-Penney model with arbitrary scattering potentials, doi: 10.1088/1367-2630/aaf9bf (2018).
- Akira Okutani, Takanori Kida, Yasuo Narumi, Tokuro Shimokawa, Zentaro Honda, Koichi Kindo, Takehito Nakano, Yasuo Nozue and Masayuki Hagiwara, High-field Magnetism of the Honeycomb-lattice Antiferromagnet Cu2(pymca)3(ClO4), doi:10.7566/JPSJ.88.013703 (2018).
- Tomonari Mizoguchi, Ludovic D. C. Jaubert, Roderich Moessner, and Masafumi Udagawa, Magnetic clustering, half-moons, and shadow pinch points as signals of a proximate Coulomb phase in frustrated Heisenberg magnets, doi: 10.1103/PhysRevB.98.144446 (2018).
- Han Yan, Rico Pohle, and Nic Shannon, Half moons are pinch points with dispersion, doi: 10.1103/PhysRevB.98.140402 (2018).
- Vilmos Kocsis, Karlo Penc, Toomas Rõõm, Urmas Nagel, Jakub Vít, Judit Romhányi, Yusuke Tokunaga, Yasujiro Taguchi, Yoshinori Tokura, István Kézsmárki, and Sándor Bordács, Identification of Antiferromagnetic Domains Via the Optical Magnetoelectric Effect, doi: 10.1103/PhysRevLett.121.057601 (2018).
- Owen Benton, L. D. C. Jaubert, Rajiv Singh, Jaan Oitmaa, and Nic Shannon, Quantum spin ice with frustrated transverse exchange: from pi-flux phase to nematic quantum spin liquid, doi: 10.1103/PhysRevLett.121.067201 (2018).
- Romain Sibille, Nicolas Gauthier, Han Yan, Monica Ciomaga Hatnean, Jacques Ollivier, Barry Winn, Geetha Balakrishnan, Michel Kenzelmann, Nic Shannon, and Tom Fennell, Experimental signatures of emergent quantum electrodynamics in a quantum spin ice, doi: 10.1038/s41567-018-0116-x (2018).
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
Invited Talks at Conference
- Nic Shannon "Living on the edge: topological phases and multiple phase competition in pyrochlore oxides" APS March Meeting, Boston, USA (2019.03.06)
- Matthias Gohlke "Dynamical and Topological Signatures of the Kitaev-Model in a [111] Magnetic Field" APS March Meeting, Boston, USA (2019.03.04)
- Nic Shannon "A hitchiker's guide to frustrated magnets" ICAM-NCTS Frontiers of Condensed Matter Workshop, Hsinchu, Taiwan (2019.01.18)
- Judit Romhanyi "Spin-orbit dimers and non-collinear phases in d1 cubic double perovskites" Workshop, Correlated Electrons in Transition-Metal Compounds: New Challenges, MPIPKS, Germany (2018.11.07)
- Tokuro Shimokawa "フラストレートしたハニカム格子反強磁性体に現れる波紋秩序状態" 基研研究会「スピン系物理の最前線」, Yukawa Institute for Theoretical Physics, Kyoto University (2018.11.02)
- Judit Romhanyi "Topologically nontrivial excitations in dimerized Quantum magnets" Correlated Magnetism: From Frustration To Topology, Dresden, Germany (2018.11.02)
- Nic Shannon "Frustrating Quantum Spin Ice" Workshop on Spin-orbit Coupled Topological States, APCTP, Postech, Korea (2018.10.01)
- Judit Romhanyi "Hall Effect of Triplons in a Dimerized Quantum Magnet" JPS 2018 Autumn Meeting, Doshisha University, Kyoto, Japan (2018.09.09)
- Judit Romhanyi "Spin-Orbit Dimers and Non-Collinear Phases in d1 Cubic Double Perovskites" Workshop: Quantum Magnetism: Frustration, Low-dimensionality, Topology, Beijing, China (2018.08.31)
- Judit Romhanyi "Spin-Orbit Dimers and Non-Collinear Phases in d1 Cubic Double Perovskites " ICM 2018, San Francisco, USA (2018.07.17)
- Judit Romhanyi "Topological bands and multipolar edge states in Q uantum magnets" HFM 2018, University of California, Davis, USA (2018.07.14)
Contributed Talks
- Tokuro shimokawa "Finite-temperature properties of the S=1/2 bilayer breathing-kagome Heisenberg magnet" JPS Meeting, Fukuoka, Japan (2019.03.14)
- Nic Shannon "Fracton and Holography" APS March Meeting, Boston, USA (2019.03.08)
- Tokuro Shimokawa "Ripple state in the frustrated honeycomb-lattice antiferromagnet" APS March Meeting, Boston, USA (2019.03.06)
- Han Yan “Francton Topological Order and Holography” KEK Theory workshop 2018, KEK, Tsukuba, Japan (2018.12.19)
- Tokuro Shimokawa "フラストレートハニカム格子反強磁性体に現れる波紋秩序状態 (Ripple state in a frustrated honeycomb-lattice Heisenberg antiferromagne)" JPS 2018 Autumn Meeting, Doshisha University, Kyoto, Japan (2018.09.10)
- Andreas Thomasen "When Three is a Crowd: Entanglement of Quantum Spins on Tripartite Lattices" ICM 2018, San Francisco, USA (2018.07.16)
- Nic Shannon "Frustrating Quantum Spin Ice" HFM 2018, University of California, Davis, USA (2018.07.10)
Seminars
- Matthias Gohlke "Topological and Dynamical Signatures of the Kitaev-Model in a [111] Magnetic Field" University of Toronto, Canada (2019.03.11)
- Geet Rakala "Triangular lattice Ising antiferromagnet with further neighbor interactions" Technical University of Munich, Munich, Germany (2019.03.04)
- Nic Shannon "An Introduction to quantum spin nematics"John Hopkins University, Baltimore, USA (2019.03.01)
- Geet Rakala "'Z6 parafermions on the triangular lattice" École normale supérieure, Paris, France (2019.02.19)
- Nic Shannon "A Hitchiker's Guide to Frustrated Magnes" Colloquium, Radboud University, Nijmegen, Netherlands (2019.02.19)
- Nic Shannon "An Introduction to quantum spin nematics" Colloquium, Technical University Munich, Germany (2019.1.10)
- Han Yan "Francton Topological Order and Holography" Institute for Quantum Information and Matter, California Institute of Technology, USA (2018.11.15)
- Tokuro Shimokawa "フラストレートしたハニカム格子磁性体に現れる新奇な磁性現象" University of Hyogo, Hyogo, Japan (2018.11.28)
- Nic Shannon "An Introduction to quantum spin nematics" Ludwig Maxmillian University, Munich, Germany (2018.11.23)
- Nic Shannon "An Introduction to quantum spin nematics" Colloquium, Ruehr Universitaet Bochum, Germany (2018.11.11)
- Han Yan "Fracton and Holography" Geballe Laboratory for Advanced Materials (GLAM), Stanford University, USA (2018.07.17)
- Han Yan "Breaking the walls of exotic quantum state of matter" Tokyo University, Tokyo, Japan (2018.05.12)
- Han Yan "Fracton Topological Order: Toy Models of Holography?" YITP, Kyoto University, Kyoto, Japan (2018.05.8 & 2018.05.10)
Poster Presentations
- Han Yan "Fracton topological order and holography" Summer School on Collective Behaviour in Quantum Matter, ICTP, Italy (2018.09.12)
- Geet Rakala "Z6 parafermions on the triangular lattice" HFM 2018, University of California, Davis, USA (2018.07.13)
- Kimberly Remund "Semi-classical equations of motion for spin nematics" HFM 2018, University of California, Davis, USA (2018.07.13)
- Tokuro Shimokawa "Ripple state in the J1-J2 classical honeycomb-lattice Heisenberg antiferromagnet" HFM 2018, University of California, Davis, USA (2018.07.13)
- Andreas Thomasen "When Three is a Crowd: Entanglement of Quantum Spins on Tripartite Lattices" HFM 2018, University of California, Davis, USA (2018.07.13)
- Christina Lee "Magnetic Analogs of the Haldane Model" HFM 2018, University of California, Davis, USA (2018.07.11)
- Soshi Mizutani "Machine learning meets quantum spin-dynamics : improving the resolution of the dynamical spin structure factor in tDMRG calculation" HFM 2018, University of California, Davis, USA (2018.07.11)
- Han Yan "Unification of Pinch-Points and Half Moons in U(1) Spin Liquids" HFM 2018, University of California, Davis, USA (2018.07.11)
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
Seminar
6.1 Thermal Hall effect from neutral currents in quantum magnets
- Date: March 18, 2019
- Venue: OIST Campus Lab2
- Speaker: Dr. Max Hirschberger (RIKEN, Center for Emergent Matter Science, Japan)
6.2 Topological magnons in Kitaev magnets at high fields
- Date: March 8, 2019
- Venue: OIST Campus Lab1
- Speaker: Prof. Karlo Penc (Wigner Research Centre for Physics, Budapest, Hungary)
6.3 Randomness induced quantum spin liquids in frustrated magnets
- Date: January 22, 2019
- Venue: OIST Campus Lab1
- Speaker: Prof. Hikaru Kawamura (Osaka University, Japan)
6.4 Cluster-Based Haldane States in Spin-Cluster Chains
- Date: January 15, 2019
- Venue: OIST Campus Lab1
- Speaker: Dr. Manuel Valiente (Institute for Advanced Study, Tsinghua University, Beijing, China)
6.5 Randomness induced quantum spin liquids in frustrated magnets
- Date: January 22, 2019
- Venue: OIST Campus Lab1
- Speaker: Dr. Takanori Sugimoto (Tokyo University of Science, Japan)
6.6 Emergence of topological gauge theories from coupled arrays of wires - coupled-wire construction demystified
- Date: October 11, 2019
- Venue: OIST Campus Ctr bldg.
- Speaker: Prof. Keisuke Totsuka (Kyoto University, Japan)
6.7 Trapping Visons in Kitaev’s spin liquid
- Date: October 10, 2019
- Venue: OIST Campus Lab 3
- Speaker: Prof. Masafumi Udagawa (Gakushuin University, Japan)
6.8 Spin-nematic state in two-dimensional frustrated spin systems consisting of ferromagnetic dimers
- Date: September 27, 2019
- Venue: OIST Campus Lab 3
- Speaker: Prof. Toshiya Hikihara (Gunma University, Japan)
6.9 Nonsymmorphic crystal and topological phases of matters
- Date: September 14, 2019
- Venue: OIST Campus Lab 1
- Speaker: Prof. SungBin Lee (Korea Advanced Institute of Science and Technology, Korea)
6.10 Topology and transport in inversion asymmetric crystals
- Date: August 24, 2019
- Venue: OIST Campus Lab 1
- Speaker: Assistant Prof. Yutaka Akagi (The University of Tokyo, Japan)
6.11 Topological Invariant for Magnon Hall Systems with Disorder
- Date: July 30, 2019
- Venue: OIST Campus Lab 3
- Speaker: Prof. Shuichi Murakami (Tokyo Institute of Technology, Japan)
6.12 Discrete Scale Invariance in Topological Semimetals
- Date: July 3, 2019
- Venue: OIST Campus Lab 1
- Speaker: Prof. Robert Joynt (University of Wisconsin-Madison, USA)
6.13 j=3/2 Quantum Spin-Orbital Liquids
- Date: June 14, 2019
- Venue: OIST Campus Lab 3
- Speaker: Mr. Willian Natori (PhD Student, University of São Paulo, Brazil)
6.14 Theory of Thermal Hall Effect
- Date: June 12, 2019
- Venue: OIST Campus Lab 1
- Speaker: Dr. Atsuo Shitade (Special PostDoctoral Researcher, RIKEN, Japan)
6.15 Experimental signatures of quantumness in rare-earth pyrochlores
- Date: June 7, 2019
- Venue: OIST Campus Lab 3
- Speaker: Dr. Romain Sibille (Instrument scientist, Paul Scherrer Institute, Switzerland)
6.16 Geometric transport in Quantum Hall Effect
- Date: Apr 19, 2019
- Venue: OIST Campus Lab 3
- Speaker: Prof. (Paul Wiegmann -The University of Chicago, USA)
6.17 The ground states of two-dimensional SU(N) Heisenberg models
- Date: Apr 10, 2019
- Venue: OIST Campus Lab 1
- Speaker: Prof. Karlo Penc (Wigner Research Centre for Physics, Budapest, Hungary)
Lecture series
6.18 Field-theory approach to quantum many-body systems
- Date: Apr 13-18, 2019
- Venue: OIST Campus Lab 3
- Speaker: Prof. Masaki Oshikawa (ISSP, The University of Tokyo, Japan)
7. Other
Nothing to report.



