FY2022 Annual Report

Mechanics, and Materials Unit
Professor Eliot Fried

 

Abstract

FY2022 was another productive year for the Mechanics and Materials Unit. During this period, unit members published 9 peer-reviewed journal articles and 1 peer-reviewed book chapter, submitted an application for 1 US patent, and gave 5 oral or poster presentations. They also contributed to various outreach activities in Okinawa. The unit also hosted 4 seminar speakers and organized the International Conference on Geometric Modeling and Processing (GMP2022).

1. Staff

As of March 31, 2023

• Dr. Eliot Fried, Professor
• Dr. Stoffel Janssens, Staff Scientist
• Dr. Vikash Chaurasia, Postdoctoral Scholar
• Dr. Vishesh Bhat, Postdoctoral Scholar
• Dr. Smriti, Postdoctoral Scholar
• Dr. David Vazquez Cortes, Research Unit Technician
• Mr. Michael Grunwald, Research Unit Technician
• Mr. Geoffry Acoba Garcia, Graduate Student
• Mr. Ali Rahmani, Graduate Student
• Ms. Akyl Shakir, Graduate Student
• Mr. Victor Carlos Teixeira, Research Intern
• Ms. Mai Barnes, Research Unit Administrator

Alumni

• Dr. Burhannudin Sutisna, Postdoctoral Scholar
• Dr. Darius Diogo Barreto, Postdoctoral Scholar
• Dr. Johannes Schönke, Staff Scientist
• Ms. Mona Kanso, Research Intern
• Mr. Rakhmetolla Rakhmanov, Research Intern
• Mr. Shreyas Samudra, Research Intern
• Mr. Joel Meier, Research Intern
• Mr. Sutashu Tomonaga, Research Intern
• Mr. Alexandru Mihai, Graduate Student
• Mr. Dmitrii Koldaev, Graduate Student

2. Collaborations

2.1 Wrinkling of nanocrystalline diamond films through compressive strain

• Type of collaboration: Joint research
• Researchers:
  • Professor Yi-Chao Chen, University of Houston, Houston, TX, USA
  • Professor Ken Haenen, Hasselt University, Hasselt, Belgium
  • Professor Paulius Pobedinskas, Hasselt University, Hasselt, Belgium

2.2 Diamond MEMS for sensing applications

• Type of collaboration: Joint research
• Researchers:
  • Dr. Meiyong Liao, National Institute for Materials Science, Tsukuba, Japan
  • Dr. Satoshi Koizumi, National Institute for Materials Science, Tsukuba, Japan

2.3 Modeling of size-dependent crystal plasticty in TRIP steel

• Type of collaboration: Joint research
• Researchers:
  • Professor Takeshi Iwamoto, Academy of Science and Technology, Hiroshima University, Japan

2.4 Flows of thin films on curved substrates

• Type of collaboration: Joint research
• Researchers:
  • Professor Daisuke Takagi, University of Hawaii at Mānoa, USA

2.5 Coupling between bulk diffusion and surface reaction diffusion

• Type of collaboration: Joint research
• Researchers:
  • Professor Fernando Duda, Federal University of Rio de Janeiro, Brazil
  • Mr. Francesco S. Forte Neto, Federal University of Rio de Janeiro, Brazil

2.6 Effects of incompatibility in fluid flows

• Type of collaboration: Joint research
• Researchers:
  • Professor Roger Fosdick, University of Minnesota, USA

2.7 Microscopic models for the rheological properties of novel suspensions

• Type of collaboration: Joint research
• Researchers:
  • Professor A. Jeffrey Giacomin, Queen's University
  • Ms. Mona Kanso, Queen's University

2.8 Unstretchable two-dimensional materials

• Type of collaboration: Joint research
• Researchers:
  • Professor Yi-Chao Chen, University of Houston, Houston, TX, USA
  • Professor Roger Fosdick, University of Minnesota, Minneapolis, MN, USA
  • Professor Brian Seguin, Loyola University Chicago, IL, USA

2.9 Flow and microphase separation of diblock copolymer melts

• Type of collaboration: Joint research
• Researchers:
  • Professor Fernando Duda, Federal University of Rio de Janeiro, Brazil
  • Mr. Victor Carlos Teixeira, Federal University of Rio de Janeiro, Brazil 

3. Activities and Findings

3.1 Kinematic chains with preserved mobility for arbitrary arrangements of their links

In this research effort, we focused on studying kinematic chains composed of links that follow a specific proportionality rule concerning their lengths and twist angles. By introducing the concept of exchange symmetry for these links, we made significant progress toward understanding how mechanisms consisting of open and closed chains of rigid links that are connected by revolute hinges move and function. Our findings offer insights into the behavior of well-known overconstrained mechanisms, such as Bennett's four-bar linkage, and also provide a comprehensive explanation for the mobility of a recently discovered class of complex, yet flexible, mechanisms. These advancements have significant implications for the fields of kinematics and machine design. The impact of our research extends across various industries. One key discovery we made is the ability to design mechanisms consisting of fixed collections of links that can be rearranged without altering the number of internal degrees of freedom. This breakthrough opens up possibilities for creating modular mechanical systems, enabling the assembly of machines in different configurations to serve specific purposes. This has broad applications, from robotics and automation to manufacturing. To showcase the potential of our approach, we presented a representative example — a nine-hinged linkage that can be assembled in ninety-four distinct ways, each with precisely one internal degree of freedom. This choice illustrates the versatility and adaptability of modular systems based on our understanding of kinematic chains and exchange symmetry. Our research pushes the boundaries of traditional mechanical design by introducing innovative principles. It sets the stage for transformative advancements in engineering applications, allowing the construction of modular mechanical systems with improved flexibility and reconfigurability. This has the potential to enhance efficiency, reduce costs, and increase adaptability across various industries. We hope that our findings will inspire further scientific exploration and encourage engineers and researchers to fully explore the potential of kinematic chains and exchange symmetry, leading to groundbreaking technological innovations.

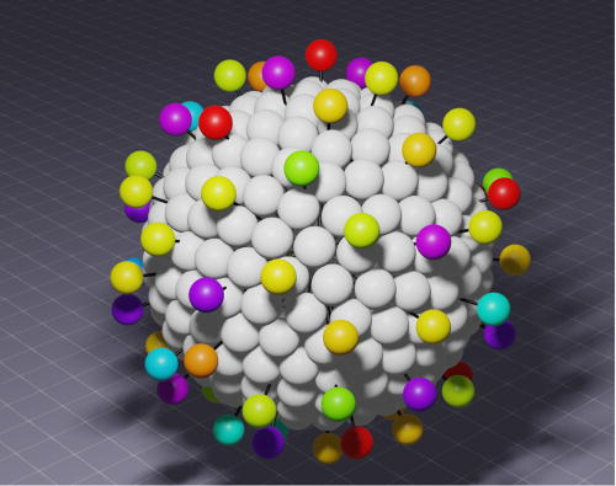
3.2 Effect of pleomorphism heterogeneity on the rotational diffusivity of the coronavirus

The commonly held notion that the coronavirus is a perfectly spherical capsid adorned with spikes fails to capture its true histological complexity. Through microscopic examination of infected patient tissues, it has been discovered that the cross sections of the viral capsids are often ellipsoidal rather than consistently spherical. Building on this understanding, we calculated the rotational diffusivity of the coronavirus when it is suspended in a liquid. Employing rigorous bead-rod theory, we developed a model by representing the spherical capsid as a sequence of beads and also by representing each spike protein as a bead. We then used energy minimization for the spreading of the spikes, charged identically, over oblate and prolate capsids. Leveraging energy minimization techniques, we systematically studied the spreading of these identically charged spikes over the oblate or prolate capsids. This analysis allowed us to explore the profound impact of coronavirus asphericity on its rotational diffusivity —a critical transport property that underlies the attachment of the virus to host cells. Our findings reveal a significant impact of the asphericity of the coronavirus on its rotational diffusivity, regardless of whether the capsid shape is oblate or prolate. Specifically, asphericityleads to a marked decrease in rotational diffusivity. This has significant implications for understanding how the virus interacts with host cells. By exploring the relationship between the shape and  rotational diffusivity of the coronavirus, our study contributes to the understanding of the fundamental properties of the virus. This knowledge may serve as a springboard for future investigations aiming to develop targeted interventions and therapies against these infectious agents. Our findings also underscore the intricate interdependence between viral morphology and its functional characteristics, providing invaluable insights that can guide the design of effective preventive measures and treatments not only for coronaviruses but also potentially for related viruses. Our ongoing research continues to explore the multifaceted nature of coronaviruses, paving the way for novel discoveries and breakthroughs toward controlling these infectious agents, ultimately safeguarding public health.

3.3 Effect of charge peplomer heterogeneity on the rotational diffusivity of the coronavirus

Recent progress in viral hydrodynamics have revolutionized our ability to calculate the transport properties of particle suspensions, including those of coronaviruses, with unprecedented accuracy. By leveraging detailed information about the shapes of viral particles, we can now employ a first-principles approach to determine their rotational diffusivity — a key parameter that governs their behavior in suspension. To accurately model the shape of a coronavirus in suspension, we approximate it by representing the spherical capsid and the radially protruding peplomers as individual beads. This bead representation allows us to apply Stokesian hydrodynamics to each bead, enabling us to calculate the rotational diffusivity of the suspension. However, accurately capturing the configuration of the cationic peplomers is crucial for obtaining reliable results. In previous studies, it was assumed that the peplomers were identical in size and charge. However, a pioneering experiment recently revealed significant heterogeneities in both the size and charge of the peplomers. Building upon this groundbreaking development, we augmented our model to incorporate the experimentally measured charge heterogeneity.
In this study, we employed energy minimization techniques to arrange the spikes, accounting for their heterogeneously charged nature, thus obtaining the precise configuration required for accurate viral hydrodynamics. We explored 20,000 randomly generated possibilities for cationic peplomers with formal charges ranging from 30 to 55. Through extensive computational analysis, we found that the resulting configurations are nearly spherically symmetric, with a slight oblate shape. The breadth of the dimensionless rotational diffusivity, a fundamental transport property that plays a pivotal role in coronavirus cell attachment, was then determined based on these configurations. Our findings shed light on the fundamental behavior of coronaviruses in suspension. By accurately capturing the shape and configuration of the peplomer components of the virus, our research contributes to a deeper understanding of their hydrodynamics. This knowledge is vital for unraveling the mechanisms underlying viral attachment to host cells and may pave the way for the development of targeted therapeutic interventions. Through computational analysis and a comprehensive exploration of various scenarios, our work advances the field of viral hydrodynamics and provides valuable insights into the transport properties of coronaviruses. By bridging the gap between theoretical models and experimental observations, we aim to foster a better understanding of viral dynamics and inspire further investigations in this critical area of research.

3.4 Isometries between given surfaces and the isometric deformation of a single unstretchable material surface

In this work, we compare the mathematical notion of isometry, which applies to abstract surfaces, and the physical concept of isometric deformation, which involves the manipulation of a tangible, unstretchable material surface. By clarifying misconceptions that have arisen in recent studies regarding the mechanics of such material surfaces, we shed light on this intriguing topic. This distinction is illustrate by two two specific examples that offer valuable insights. To fix ideas, we first revisit the distinction between isometries and isometric deformations in flat, two-dimensional space. By exploring this fundamental difference, we aim to provide a clear understanding of the concepts at hand and their implications. Additionally, we conduct a detailed analysis of the use of rectifying developable surfaces for characterizing isometric deformations of rectangular material strips. Our work not only clarifies misconceptions surrounding isometry and isometric deformation but also contributes to the broader understanding of the mechanics of unstretchable material surfaces. By bridging the gap between mathematical abstractions and physical realities, we deepen our comprehension of the interplay between geometry and physical deformations. These insights have the potential to advance various fields, including materials science, engineering, and applied mathematics. Through our exploration of these concepts and the analysis of concrete examples, we aim to provide a comprehensive and accessible explanation of the key distinctions between isometries and isometric deformations. By enhancing our collective understanding, we pave the way for further advancements in the study of material surfaces and their mechanical behavior.

3.5 A novel dimensional reduction for the equilibrium study of inextensional material surfaces

We present a comprehensive framework that enables the determination of equilibrium equations for unstretchable material surfaces with arbitrary flat reference shapes. By applying tractions or moments to the edge of the surface, we explore its deformation and establish a robust and broadly applicable methodology for capturing this behavior. Our approach relies on a representation of all possible isometric deformations of the material surface. This representation allows us to convert the bending energy associated with the surface deformation into a line integral over its edge. By employing the Euler-Lagrange equations, we derive a complete and definitive set of equilibrium equations that govern the system. These equations take the form of a system of ordinary differential equations that describe the spatial directrix of the surface. To account for potential discontinuities in the tangent and/or curvature of the surface edge, we establish jump conditions that serve as additional constraints on the system. These conditions provide valuable insights into the behavior of the surface at points where such discontinuities may arise. To illustrate the practical implications of our framework, we consider a simple yet instructive example: the deformation of a rectangular strip subject to various edge conditions. This example serves as a tangible demonstration of the efficacy and applicability of our approach. By developing this general framework and examining a specific case, we contribute to the broader understanding of equilibrium in unstretchable material surfaces. Our findings offer insights into the intricate interplay between deformation, energy, and geometric constraints. This knowledge holds potential significance in fields such as structural mechanics, materials engineering, and applied mathematics.

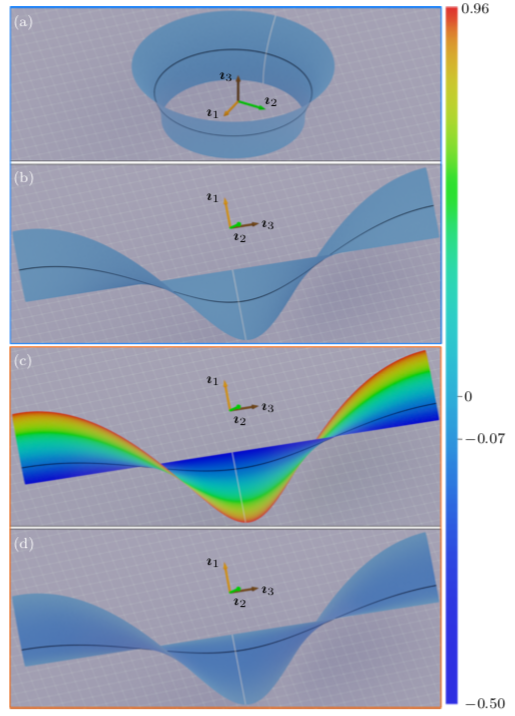
3.6 Stable Möbius bands from isometrically deformed circular helicoids

We investigate the intriguing problem of creating a ruled Möbius band using an unstretchable, homogeneous, isotropic, elastic material surface. By subjecting the material surface to an isometric and chirality-preserving deformation from a circular helicoidal reference configuration, we unveil the remarkable properties that govern the formation of such Möbius bands. Our study reveals that the geometry of the Möbius band is fully determined by the unit binormal of the Frenet frame of its midline. Specifically, the midline must be a geodesic and possess uniform torsion inversely proportional to the pitch of the helicoidal reference configuration. These geometric constraints play a crucial role in the formation of stable Möbius bands. Considering the energy density of the material surface, which depends quadratically on the mean curvature of its deformed configuration, we derive a closed-form expression for the total energy required to produce a ruled Möbius band. Remarkably, this expression reduces to a simple integral over the midline of the Möbius band, providing an exact and non-approximate description of the energy storage. To find the energetically optimal Möbius bands, we formulate and solve a constrained variational problem that considers the dimensionally reduced bending energy. By numerically solving this problem, we discover a fascinating interplay between operative constraints, leading to a multitude of stable solutions. Importantly, we determine that the number of turns in the helicoidal reference configuration serves as a key parameter, with solutions emerging only above a specific threshold that we calculate with precision. For cases where the number of half twists exceeds three, we uncover a rich diversity of stable Möbius bands with an odd number of half twists. Each of these cases exhibits an energetically optimal Möbius band, which displays rotational symmetry corresponding to its number of half twists. Intriguingly, other energy minima yield Möbius bands that lack symmetry, revealing the intricate relationship between energy optimization and geometric properties. To the best of our knowledge, this study represents the first exploration of stable Möbius bands produced through the isometric deformation of non-flat reference configurations. By unraveling the underlying principles and showcasing these novel examples, our research opens up new avenues for understanding the behavior and formation of Möbius bands beyond traditional approaches. The findings of this study not only contribute to the field of material science and elasticity but also offer insights into the broader realm of geometric structures and their mechanical properties. By expanding our knowledge of Möbius bands and their stability, we lay the groundwork for potential applications in areas such as advanced materials, engineering, and design.

3.7 Direct femtosecond laser writing of nanochannels

The fabrication of nanofluidic devices is complex, expensive, and time-consuming due to the small length scales involved. We found a method that overcomes these challenges through the direct femtosecond laser writing of nanochannels between nanocrystalline diamond films and glass substrates. We show that the writing process transforms a portion of the sample into a nanostrip and that the nanostrip is surrounded by two nanochannels formed through the delamination of the film. The height of a nanochannel is less than 100 nm, the with of a nanochannel is approximately 2 micrometers, and both dimensions are tunable through laser pulse energy. We show that the nanostrip consists of non-diamond carbon and that the glass substrate is affected by laser writing. By fabricating a nanofluidic device and performing simulations, we show that the nanochannels fill with water through capillary action. Our work paves the way for manufacturing affordable devices for applications that require robust nanochannels.

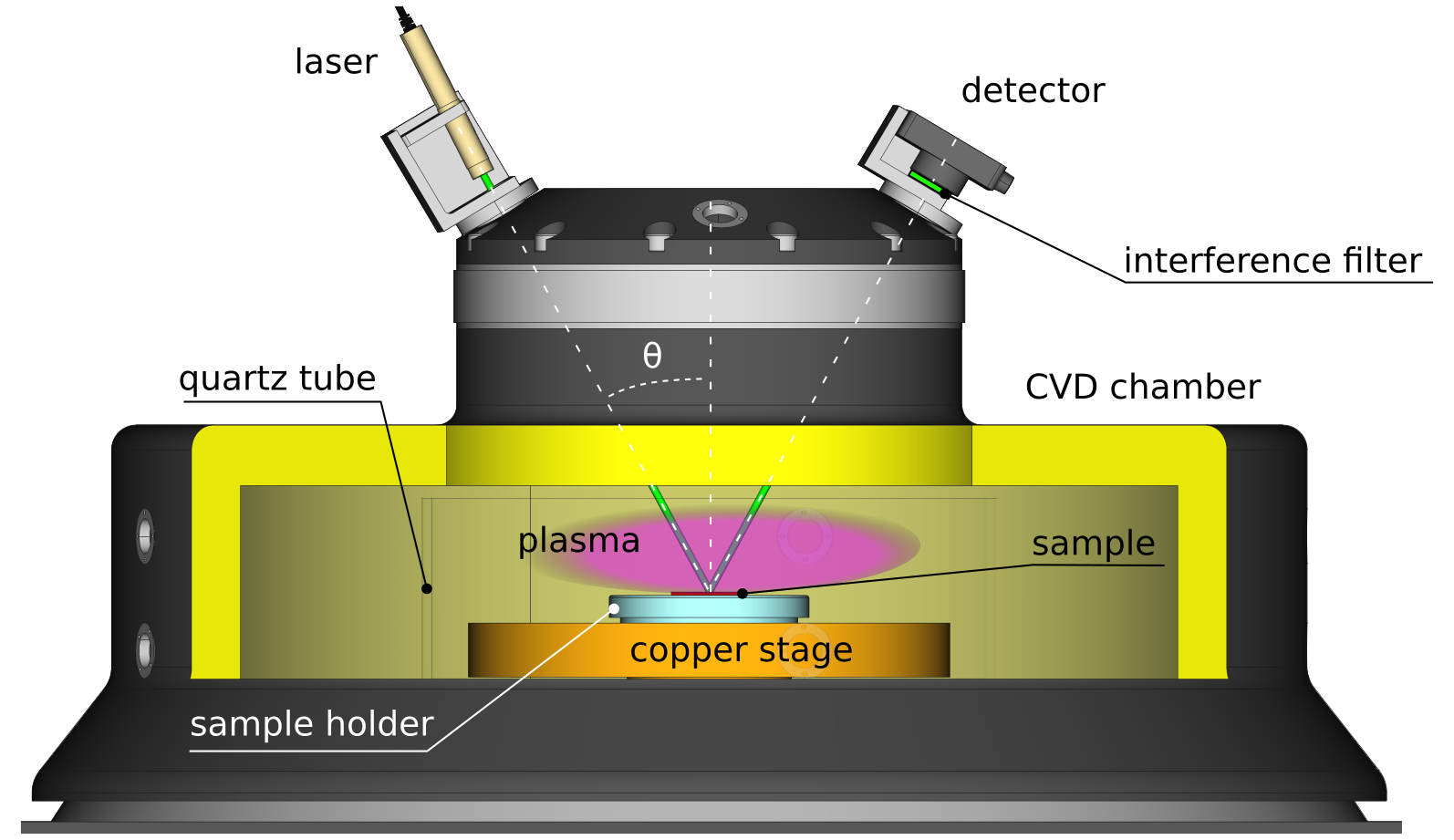
3.8 Early stages of polycrystalline diamond deposition: laser reflectance at substrates with growing nanodiamonds

The chemical vapor deposition of polycrystalline diamond (PCD) films is typically done on substrates seeded with diamond nanoparticles. Specular laser reflectance has been used in tandem with a continuous film model to monitor the thickness of these films during their deposition. However, approaches to gain information on properties that strongly affect film morphology, such as the areal density of seeds, remain largely unexplored. This work outlines a strategy for using laser reflectance measurements to refine the monitoring of film thickness during deposition, estimate the mean equivalent radii and the areal density of seeds, and estimate growth incubation periods. We present a general model based on the Rayleigh theory of scattering for laser reflectance at substrates with growing nanoparticles that captures the early stages of PCD deposition. We test our model experimentally by depositing diamond under identical conditions on silicon substrates with various seed densities and by comparing seed densities obtained by scanning electron microscopy to those determined by our strategy. We also explore the different deposition stages for which our model and a continuous film model can be used safely. In addition to providing guidelines for characterizing PCD deposition, this work may also advance the general understanding of nanoparticle growth and formation.

3.9 Mathematical description of bending mechanics of origami like structures

This work has developed a mathematical model to predict the shape of a thin sheet-like material with a crease under applied forces and torques. The model is based on a reformulation of existing models, then extended by introducing a ”joint-condition”. Differential equations are derived and then solved numerically. In addition to theoretical work, a novel experimental apparatus to test folded sheets was designed and built. This apparatus allows for various boundary conditions to be applied to a folded sheet, then photographed for comparison with theory. The current work is currently being refined into a publication.

4. Publications

4.1 Journals

1. V. Chaurasia, E. Fried. Stable Möbius bands from isometrically deformed circular helicoids, Journal of Elasticity, in press. (doi:10.1007/s10659-023-10008-x)
2. Y.-C. Chen, E. Fried. Conformal deformations of a dilational material surface, Journal of Elasticity, in press. (doi:10.1007/s10659-023-10003-2)
3. V. Chaurasia, M. Kanso, E. Fried, A.J. Giacomin. Coronavirus peplomer charge heterogeneity, Physics of Fluids 35 (2023), 037125-1–10. (doi:10.1063/5.0140851)
4. D. Vázquez-Cortés, S. D. Janssens, B. Sutisna, E. Fried. Early stages of polycrystalline diamond deposition: laser reflectance at substrates with growing nanodiamonds, Nanoscale Advances 5 (2023), 412–424. (doi:10.1039/D2NA00723A)
5. Y.-C. Chen, R. Fosdick, E. Fried. A novel dimensional reduction for the equilibrium study of inextensional material surfaces, Journal of the Mechanics and Physics of Solids 169 (2022), 105068-1–27. (doi:10.1016/j.jmps.2022.105068)
6. Y.-C. Chen, R. Fosdick, E. Fried. Isometries between given surfaces and the isometric deformation of a single unstretchable material surface, Journal of Elasticity 151 (2022), 159–175. (doi:10.1007/s10659-022-09909-0)
7. M.A. Kanso, M. Naime, V. Chaurasia, K. Tontiwattanakul, E. Fried, A.J. Giacomin. Coronavirus pleomorphism, Physics of Fluids 34 (2022), 063101-1–10. (doi:10.1063/5.0094771)
8. Y.-C. Chen, R. Fosdick, E. Fried. Reply to van der Heijden and Starostin,  Proceedings of the Royal Society of London Series A, Mathematical, Physical and Engineering Sciences, 478 (2022), 20210856-1–9. (doi:10.1098/rspa.2021.0856)
9. J. Schönke, M. Forsberg Conde, E. Fried. Kinematic chains with preserved mobility for arbitrary arrangements of their links, Mechanism and Machine Theory 175 (2022), 104921-1–9. (doi:10.1016/j.mechmachtheory.2022.104921)

4.2 Books and other one-time publications

1. C.S. Aravinda, V.S. Bhat. Basic ergodic theory. In: Elements of Dynamical Systems (A. Nagar, R. Shah, S. Sridharan, Eds.). Springer Texts and Readings in Mathematics 79 (2022), 73–107. (doi:10.1007/978-981-16-7962-9_3)

4.3 Presentations

4.3.1 Oral Presentations

1. S. D. Janssens, D. Vázquez-Cortés, and E. Fried. Two-dimensional simulations of nanocrystalline diamond film growth, NDNC 2022, Bunka Hall, Kanazawa, Japan, Hybrid, June 6–9, 2022.

2. E. Fried. Impact of Peplomer Charge Heterogeneity on the Rotational Diffusivity of a Suspension of Coronavirions, Recent Trends in Microrheology and Microfluidics, OIST, Okinawa, Japan, January 10-12, 2023

4.3.2 Other Presentations

1. David Vázquez-Cortés, Stoffel D. Janssens, Burhannudin Sutisna, and Eliot Fried. Laser reflectance at the early stages of diamond deposition on seeded silicon substrates. Poster presentation at the Hasselt Diamond Workshop 2023 - SBDD XXVII in Hasselts, Belgium. March 15-17, 2023

2. S. D. Janssens, V. Chaurasia, and E. Fried. Effect of a surface tension imbalance on a partly submerged cylinder, Recent Trends in Microrheology and Microfluidics, OIST, Okinawa, Japan, January 10-12, 2023

3. David Vazquez-Cortes, Stoffel Dominique Janssens, and Eliot Fried. Early stages of polycrystalline diamond growth studied by laser reflectance. Poster presentation at the 15th International Conference on New Diamond and Nano Carbons (NDNC2022) in Kanazawa, Japan. June 6-9, 2022

5. Intellectual Property Rights and Other Specific Achievements

5.1 KAKENHI: Grant-in-Aid for Scientific Research

Staff Scientist: Dr. Stoffel D. Janssens
Period: From April 2021

5.2 International advisory board for NDNC 2023

Dr. Stoffel Janssens is a member of the international advisory board of the 16th New Diamond and Nano Carbons (NDNC) Conference, Michigan State University, East Lansing, MA, USA, June 18–22.

6. Meetings and Events

6.1 Meetings

6.1.1 Seminars
 

6.1.2 Long Term Visiting Researcher

• Professor Yi-chao Chen, University of Houston

6.2 Events

6.2.1 International Conference on Geometric Modeling and Processing (GMP2022)

• Date: May 11, 2022
• Venue: Zoom

7. Other

7.1 OIST Press Release: The shape of coronavirus affects its transmission, finds study

Aglobal research team, including scientists from Queen’s University, Canada, and Mechanics and Materials Unit, OIST have modeled how the different elliptical shapes affect the way these viral particles rotate within fluids, impacting how easily the virus can be transmitted. The study was published recently in Physics of Fluids.

See more at "The shape of coronavirus affects its transmission, finds study."
which was released on August 31, 2022