Publication - LIMDD: A Decision Diagram for Simulation of Quantum Computing Including Stabilizer States

12 September 2023

Quantum 7, 1108 (2023). Link to publication.

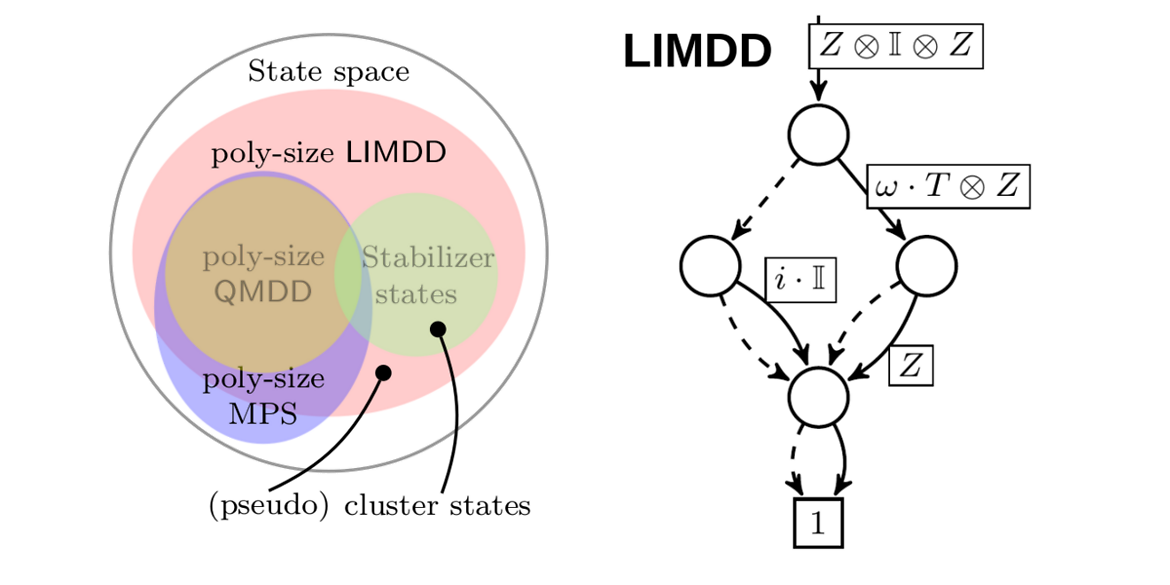
Efficient methods for the representation and simulation of quantum states and quantum operations are crucial for the optimization of quantum circuits. Decision diagrams (DDs), a well-studied data structure originally used to represent Boolean functions, have proven capable of capturing relevant aspects of quantum systems, but their limits are not well understood. In this work, we investigate and bridge the gap between existing DD-based structures and the stabilizer formalism, an important tool for simulating quantum circuits in the tractable regime. We first show that although DDs were suggested to succinctly represent important quantum states, they actually require exponential space for certain stabilizer states. To remedy this, we introduce a more powerful decision diagram variant, called Local Invertible Map-DD (LIMDD). We prove that the set of quantum states represented by poly-sized LIMDDs strictly contains the union of stabilizer states and other decision diagram variants. Finally, there exist circuits which LIMDDs can efficiently simulate, while their output states cannot be succinctly represented by two state-of-the-art simulation paradigms: the stabilizer decomposition techniques for Clifford + T circuits and Matrix-Product States. By uniting two successful approaches, LIMDDs thus pave the way for fundamentally more powerful solutions for simulation and analysis of quantum computing.