"Fung-Type Elastic Potentials in Biomechanics: (Missing) Theory and (Further) Applications" Professor Salvatore Federico

Dear All,

Mathematical Soft Matter Unit (Fried Unit) would like to invite you to a Seminar by Professor Salvatore Federico from the Universiy of Calgary.

-------------------------------------------
Date: Wednesday, May 13, 2015
Time: 10:30-11:30
Venue: C210, LevelC, Center building
-------------------------------------------

Speaker:
Professor Salvatore Federico
The University of Calgary

Title: 
Fung-Type Elastic Potentials in Biomechanics: (Missing) Theory and
(Further) Applications

Abstract:

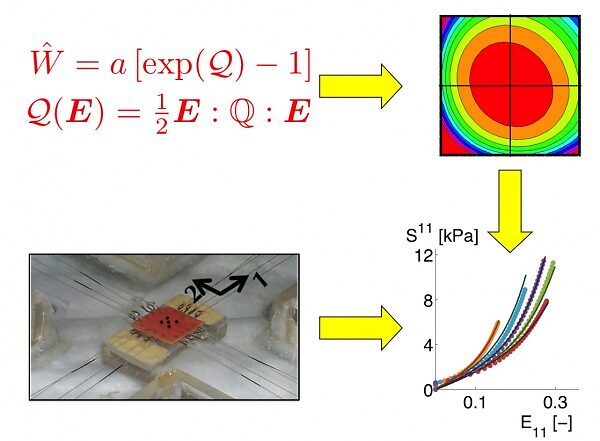
The anisotropic, non-linear elastic behaviour of soft biological tissues is typically accounted for by the hypothesis of hyperelasticity, i.e., the existence of an elastic potential from which a certain measure of stress is obtained by differentiation with respect to the conjugate strain. Fung's potentials, based on the exponential of a quadratic form in the components of the Green-Lagrange strain, have been widely used in soft tissue modelling, and have inspired the potentials known as Fung-type, in which the exponential was replaced by other monotonically increasing functions. It has been shown that simple fitting of the parameters of a Fung-type potential to experimental stress-strain curves may lead to non-convexity, with undesirable effects on the reliability of the algorithms used in Finite Element simulations.

We proved that the necessary and sufficient condition for the strict convexity of a Fung-type potential is that the quadratic form in the exponential is positive definite. This result also provides a clear physical meaning for the parameters featuring in the quadratic form, in terms of their relationship with the small-strain elastic moduli.

Moreover, we derived the correct form of the fourth-order tensor of the quadratic form for the case of incompressibility, which was obtained by means of an appropriate algebraic decomposition of the tensor.

We also applied this class of potentials to the mechanical characterisation of the human atrium, and succeeded in discriminating among experimental bi-axial test protocols with different ratios between the two orthogonal tensions.

Speaker profile: http://www.ucalgary.ca/federico/