FY2018 Annual Report

Unit members and guests of "Computational problems in low-dimensional topology" mini-sympoisum
1. Staff
- Dr. Anastasiia Tsvietkova, Assistant Professor
- Dr. Tirasan Khandhawit, Postdoctoral Scholar
- Dr. Dale Koenig, Postdoctoral Scholar
- Dr. Robert Tang, Postdoctoral Scholar
- Dr. Nicholas Owad, Postdoctoral Scholar
- Dr. Linling Lu, Visiting Researcher
- Mr. Burns Thomas,Graduate Student
- Mr. Haider Touseef, Graduate Student
- Mr. Castellano Felipe, Research Intern
- Mr. Robert Hanson, Research Intern
- Ms. Yukiko Nakagawa, Research Unit Administrator
- Ms. Ayumi Shimojima, Research Unit Administrator
2. Collaborations
- Dr. Oliver Dasbach (Louisiana State University)
- Dr. Joel Hass (University of California, Davis)
- Dr. Jane Gilman (Rutgers University, Newark)
- Dr. Abigail Thompson (University of California, Davis)
- Dr. Kathleen Peterson (Florida State University)
- Dr. Marc Lackenby (Oxford University)
- Dr. Jessica Purcell (Monash University)
- Dr. Valentina Disarlo (Heidelberg Universität)
- Dr. Max Forester (University of Oklahoma, USA)
- Dr. Anja Randecker (University of Toronto)
- Dr. Jing Tao (University of Oklahoma, USA)
- Dr. Jianfeng Lin (Massachusetts Institute of Technology)
- Dr. Hirofumi Sasahira (Kyushu University)
3. Selected Projects and Findings

Figure 1: A tiling of the hyperbolic plane (dimension 2).

Figure 2: A tiling of the hypebolic space (dimension 3).

Figure 3: A trefoil knot and a minimal Seifert surface.
3.1 Lower Bounds on the Computational Complexity of Link Problems
Knots and links can be distinguished by computing mathematical properties of the link, often expressed by polynomials or integers, called "invariants". Some of the most famous and oldest invariants are thought to be very hard to compute, but until recently very little has been known about their actual algorithmic complexity. We proved that several naturally arising problems in the knot theory are NP-hard, and thus are provably computationally difficult modulo P=NP.
3.2 Seiberg-Witten Floer spectra and Bauer-Furuta invariants
In past decades, gauge theory has been one of the important tools to study 3-manifolds and 4-manifolds. The Seiberg-Witten invariant can distinguish non-diffeomorphic 4-manifolds of the same homeomorphism type. The Seiberg-Witten Floer homology gives deep insight of a 3-manifold. We study stable homotopy refinement of these invariants which provide more information about the manifold. One of the activities is to extend Manolescu's construction of Seiberg-Witten Floer spectra to general 3-manifolds, and find a formula to compute a stable homotopy refinement of the Seiberg-Witten invariant, also known as the Bauer-Furuta invariant, of a 4-manifold decomposed along a 3-manifold. Another direction is to find a refinement for a parametrized version of the Seiberg-Witten invariant. As one of the applications, we find new examples of 4-manifolds whose space of positive scalar curvature metrics has nontrivial homotopy group.
3.3 Straight knots
Diagrammatic invariants of knots have interesting relations to the geometry and topology of the respectiove 3-manifold, which is a knot complement in 3-sphere. We suggest a new diagrammatic invariant called the straight number of a knot. Using the high performance computing cluster at OIST, we enumerated all knots with 10 or less crossings and computed their straight number. We will investigate the relation between straight number and hyperbolic volume more, as well as look for connections with other invariants. We are developed a new random model for links based on their straight representation.
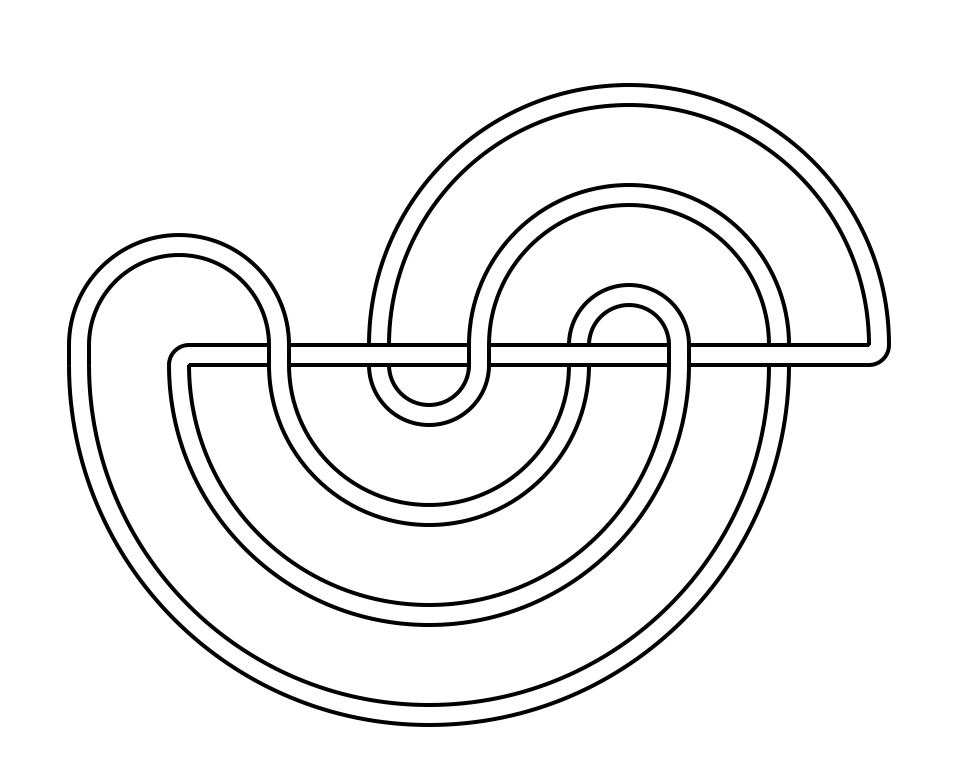
A straight knot
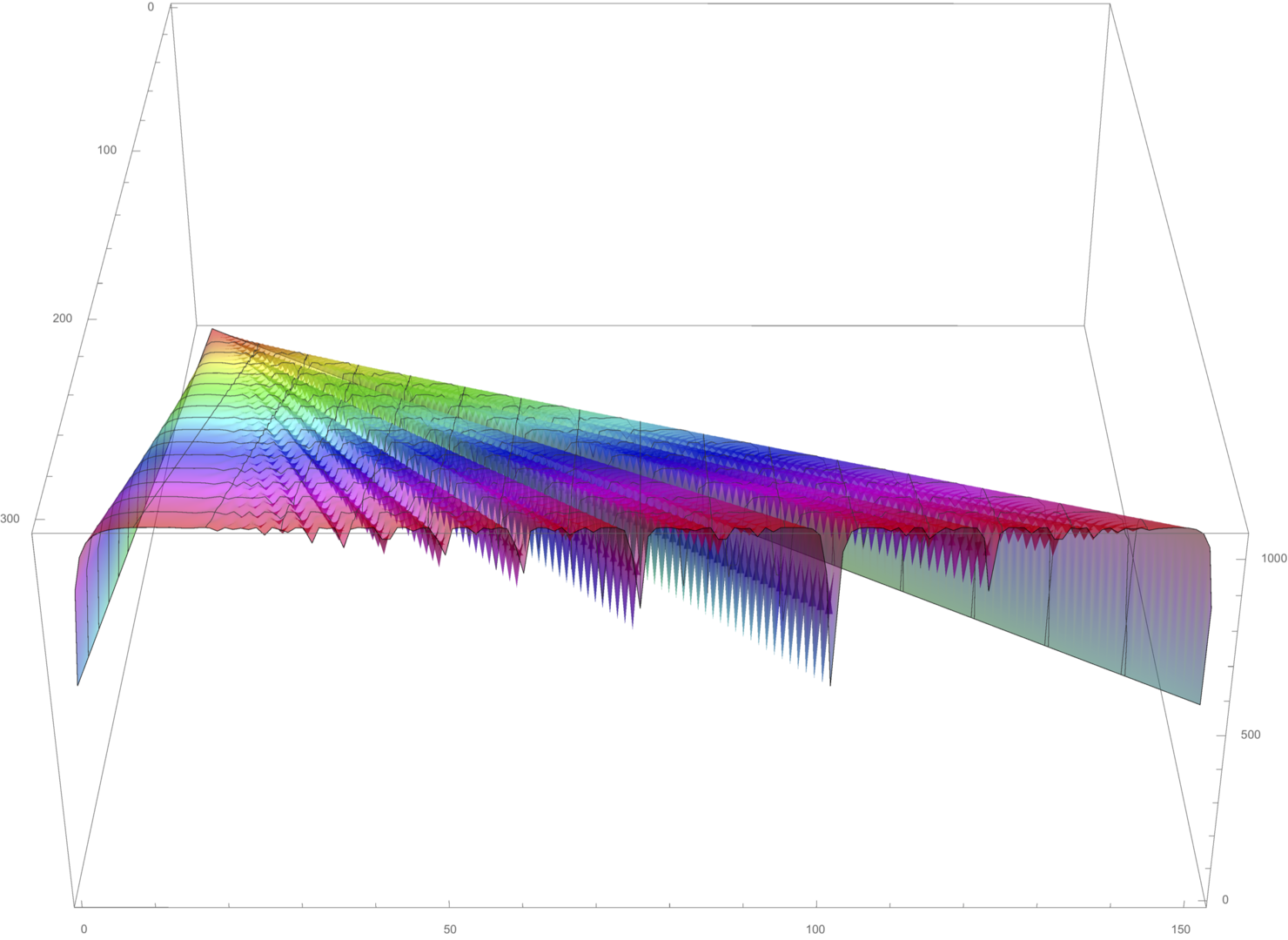
A graph of volume's relation to straight number.
3.4 The number of surfaces of fixed genus in 3-manifolds.
The presence of embedded surfaces in a 3-manifold often gives information about this manifold. We show that the number of closed incompressible surfaces of fixed genus in the complement of a prime alternating link in 3-sphere is at most polynomial in the number of crossings. Previously, only exponential bounds were known for a number of surfaces in a 3-manifold. We also prove the result of a similar nature for spanning surfaces (including Seifert surfaces). All this can be extended to wider classes of links: links that are alternating on surfaces rather than on a projection plane, and in an arbitrary 3-manifold rather than a 3-sphere only. Then we consider the number of surfaces of fixed genus in a arbitrary huyperbolci 3-manifold; it turns out, it is polynomial in volume. The proof techniques involve geometric topology and differential geometry.
4. Publications
4.1 Journals
- Forester, M., Tang, R. and Tao, J. Veech surfaces and simple closed curves. Israel Journal of Mathematics 223, 323-342, (doi:doi:https://doi.org/10.1007/s11856-017-1617-5) (2018).
- Lin, J. and SASAHIRA, H. and Khandhawit, T. Unfolded Seiberg-Witten Floer spectra, II: Relative invariants and the gluing theorem. arXiv 1809.09151 (2018).
- Koenig, D. Trisections of 3-Manifolds. arXiv 1805.11276 (2018).
- Koenig, D. 3-manifolds lying in trisected 4-manifolds. arXiv 1806.04870 (2018).
- Disarlo, V., Randecker, A. and Tang, R. Rigidity of the saddle connection complex. arXiv 1810.00961 (2018).
- Koenig, D., and Tsvietkova, A. NP-hard problems naturally arising in knot theory. arXiv:1809.10334 (2018)
- Hass,J., Thompson A. and Tsvietkova, A. Alternating links have at most polynomially many Seifert surfaces of fixed genus. arXiv:1809.10996 (2018).
- Owad, N. Bridge spectra of cables of 2-bridge knots. Journal of Knot Theory and Its Ramifications Vol. 27, No. 02, (doi:https://doi.org/10.1142/S0218216518500128) (2018).
- Tsvietkova, A. Simplicial volume of links from link diagrams. Mathematical Proceedings Cambridge Philosophical Society 166 75-81, (doi:https://doi.org/10.1017/S0305004117000731) (2019).
- Tsvietkova, A. Determining isotopy classes of crossing arcs in alternating links. Asian Journal of Mathematics 22, 1005 – 1024, (doi:http://dx.doi.org/10.4310/AJM.2018.v22.n6.a2) (2019).
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Koenig, D. 3-manifolds in trisections, OIST, April 11 (2018).
- Koenig, D. Finding 3-manifolds in trisections of 4-manifolds, Spring Eastern Sectional Meeting, Northeastern University, Boston, MA, U.S.A., April 22 (2018).
- Tsvietkova, A. Using hyperbolic geometry to obtain information on knots, links and 3-manifolds, Tohoku University, April 24 (2018).
- Ru, L. A suspension flow with a Plykin attractor, OIST, May 22 (2018).
- Tsvietkova, A. The number of surfaces of fixed genus in a link complement, OIST, May 30 (2018).
- Tsvietkova, A. The number of surfaces of fixed genus in link complements, TOPOLOGY IN DIMENSIONS 3, 3.5 and 4, University of California, Berkeley, June 28 (2018).
- Koenig, D. Computationally hard problems in knot theory, OIST, August 1 (2018).
- Owad, N. Straight Number and Volume, University of Melbourne, August 8 (2018).
- Tang, R. Solving Word Problems in finitely presented groups, OIST, August 9 (2018).
- Khandhawit, T. Stable Homotopy and Differential Topology, OIST, August 16 (2018).
- Koenig, D. 3-manifolds in trisected 4-manifolds, Four Dimensional Topology, Osaka City University, September 6 (2018).
- Khandhawit, T. Gluing theorems for Bauer-Furuta invariants, Kyoto University, September 14 (2018).
- Owad, N. Straight knots, volume, and snails, Hiroshima University, Hiroshima, Japan, October 9 (2018).
- Tang, R. Cubical geometry in the polygonalisation complex, Osaka University, October 9 (2018).
- Owad, N. Straight Number and Volume, Nara Women’s University, Nara, Japan, October 13 (2018).
- Tang, R. The geometry of saddle connection complexes of translation surfaces, Nara Women's University, October 13 (2018).
- Owad, N. Straight number and its relation to other invariants, Osaka University, Osaka, Japan, October 16 (2018).
- Khandhawit, T. A relative family version of the Bauer-Furuta invariant, Kyushu University, October 19 (2018).
- Tang, R. Solving word problems in groups, University of Toronto, November 2 (2018).
- Koenig, D. 3-manifolds in trisected 4-manifolds, Osaka University, November 30 (2018).
- Owad, N. Snail links and random straight links, Naha City Traditional Arts & Craft Center, Naha, Okinawa, December 8 (2018).
- Tsvietkova, A. NP–hard problems naturally arising in knot theory, Classical and quantum three-manifold topology, Monash University, Australia, December 18 (2018).
- Owad, N. Snail links and random straight links, George Washington University, USA, January 20 (2019).
- Owad, N. Snails, random straight links, and volume, University of Nebraska–Lincoln, USA, January 23 (2019).
- Tsvietkova, A. Representations of knot groups, University of Tokyo, February 12 (2019).
- Khandhawit, T. A relative family version of the Bauer-Furuta invariant, Massachusetts Institute of Technology, USA, March 11 (2019).
- Tsvietkova, A. Representations of knot groups, Low dimensional topology and number theory XI, Osaka University, Osaka, Japan, March 11 (2019).
- Khandhawit, T. A relative family version of the Bauer-Furuta invariant, East Asian Conference on Gauge theory and Related topics, Kyoto University, Kyoto, Japan, March 27 (2019).
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Seminars
Dr. Gudrun Szewieczek (TU Wien/Kobe)
- Date: January 17, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Conformally flat hypersurfaces and Guichard nets
Prof. Luca Lussardi (Politecnico di Torino)
- Date: February 7, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: The Kirchhoff-Plateau problem
Prof. Yasha Neiman (OIST)
- Date: April 4, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Geometric Algebras: from the wedge produce to higher-spin Holography
Dr. Johannes Schonke (OIST)
- Date: April 18, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Möbius Kaleidocycles --- A New Family of Ring Mechanisms
Ms. Motoko Kato (Tokyo University)
- Date: May 9, 2018
- Venue: OIST Campus, Lab 2, B662
- Title: On groups whose actions on finite-dimensional CAT(0) spaces have global fixed points
Prof. Jessica Purcell (Monash University)
- Date: May 21, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Cusp shape and tunnel number (part 1)
Prof. Jessica Purcell (Monash University)
- Date: May 22, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Cusp shape and tunnel number (part 2)
Prof. Jessica Purcell (Monash University)
- Date: May 23, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Cusps and alternating knots
Prof. Joel Hass (UC Davis)
- Date: May24, 2018
- Venue: OIST Campus, Center Bldg, B250
- Title: Comparing shapes of genus zero
Dr. Josh Howie (Monash University)
- Date: May24, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Coiled Surfaces And The Slope Conjectures
Prof. Makoto Narita (Okinawa National College of Technology)
- Date: October 2, 2018
- Venue: OIST Campus, Lab 3, B717
- Title: Spacetime Singularities -An Introduction-
Prof. Kenta Hayano (Keio University)
- Date: October 24, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: On Diagrams of Simplified Trisections and Mapping Class Groups
Prof. Osamu Saeki (Kyushu University)
- Date: October 31, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Unlinking singular locus from regular fibers and its application to submersions
Prof. Kazuto Takao (Kyoto University)
- Date: November 7, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Morse functions and singularities of product maps
Prof. Shinobu Hikami (OIST)
- Date: November 8, 2018
- Venue: OIST Campus, Lab 3, B662
- Title: Topological gravity and intersection theory
Prof. John Loftin (Rutgers University, Newark)
- Date: November 14, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Neck pinch singularities in the geometry of surfaces
Prof. Scott Carter (University of South Alabama)
- Date: December5, 2018
- Venue: OIST Campus, Lab 3, B700
- Title: Ribbon and string representations of finite subgroups of SU(2)
Prof. Hirofumi Sasahira (Kyushu University)
- Date: January 16, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: The Seiberg-Witten equations and topology
Prof. Tadayuki Watanabe (Shimane University)
- Date: January 22, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Preliminary lecture I: Goussarov-Habiro's theory of graph surgery
Prof. Tadayuki Watanabe (Shimane University)
- Date: January 23, 2019
- Venue: OIST Campus, Lab 2, B662
- Title: Preliminary lecture II: Kontsevich's characteristic classes (Chern-Simons perturbation theory configuration space integral)
Prof. David Gabai (Princeton University)
- Date: January 23, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: The General 4 dimensional Light Bulb Theorem
Prof. Tadayuki Watanabe (Shimane University)
- Date: January 24, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Some exotic nontrivial elements of the rational homotopy groups of Diff(S^4)
Dr. Brian Seguin (Loyola University Chicago)
- Date: January 29, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: On the nonlocal curvature of surfaces and curves
Prof. Shinpei Baba (Osaka University)
- Date: January 30, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Neck-pinching of CP^1-structures
Dr. Harrison Chapman (Colorado State University)
- Date: February 18, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Alternating knots are rare
Prof. Jennifer Schultens (UC Davis)
- Date: February 20, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: The Kakimizu complex of Seifert fibered spaces
Prof. Michael Kapovich (UC Davis)
- Date: February 21, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Ramified covering maps of spheres and arboreal polygons
Prof. Dan Romik (UC Davis)
- Date: February 25, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Viazovska's work on the sphere packing problem and some recent developments in number theory
Prof. Stephan Tillmann (University of Sydney)
- Date: March 18, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Character varieties, ideal points and actions on trees
Prof. Stephan Tillmann (University of Sydney)
- Date: March 19, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Essential surfaces detected by the character variety
Prof. Ben Burton
- Date: March 20, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Topology on tiny machines: logspace and finite-state complexity
Prof. Stephan Tillmann (University of Sydney)
- Date: March 22, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Tropical geometry, normal surfaces and the character variety
Prof. Bernd Krauskopf (University of Auckland)
- Date: March 26, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Global manifolds and the transition to chaos in the Lorenz system
Prof. Hinke Osinga (University of Auckland)
- Date: March 27, 2019
- Venue: OIST Campus, Lab 3, B700
- Title: Robust chaos: a tale of blenders, their computation, and their destruction
6.2 Events
6.2.1 OIST Mini-symposia: "Computational Problems in Low-dimensional Topology"
- Date: March 12-14, 2018
- Venue: OIST Conference Center
- Speakers:
- Hyungryul Baik (Korea Advanced Institute of Science and Technology)
- Jane Gilman (Rutgers University, Newark)
- Craig Hodgson (University of Melbourne)
- Kazuhiro Ichihara (Nihon University)
- Gaven Martin (Massey University)
- Hidetoshi Masai (Tohoku University)
- Luisa Paoluzzi (Université d’Aix-Marseille)
- Carlo Petronio (UNIVERSITA' DI PISA)
- Alan Reid (Rice University)
- Dan Romik (University of California, Davis)
- Henry Segerman (Oklahoma State University)
- Ser Peow Tan (National University of Singapore)
- Christian Zickert (University of Maryland)
6.2.2 OIST Workshop: "Geometry and Topology of 3-manifolds workshop"
- Date: May 25-28, 2018
- Venue: OIST Seaside House
- Co-organizers:
- Joel Hass (University of California, Davis, USA)
- Jessica Purcell (Monash University, Melbourne, Australia)
- Speakers:
- Benjamin Burton ( University of Queensland)
- Marc Culler ( University of Illinois, Chicago)
- Oliver Dasbach ( Louisiana State University)
- David Gabai ( Princeton University)
- Chuichiro Hayashi ( Japan Women's University)
- Josh Howie (Monash University)
- Autumn Kent ( University of Wisconsin)
- Eiko Kin ( Osaka University)
- Sadayoshi Kojima ( Tokyo Institute of Technology)
- Ana Lecuona ( l'Universite d'Aix-Marseille)
- Yoav Moriah ( Technion - Israel Institute of Technology)
- Tali Pinsky ( Technion - Israel Institute of Technology)
- Hyam Rubinstein ( University of Melbourne)
- Makoto Sakuma (Hiroshima University)
- Abigail Thompson (UC Davis)
- Stephan Tillmann ( University of Sydney)
- Non-OIST participants
- Yasuhiko Asao (The University of Tokyo)
- Christopher Karl Atkinson (University of Minnesota Morris)
- Jose Manuel Ayala-Hoffmann (University of Melbourne)
- Hyungryul Baik (KAIST)
- Michael Brandenbursky (Ben Gurion University)
- Martin Jude Bridgeman (Boston College)
- Aaron Tomas Wright Calderon (Yale University)
- Richard Canary (University of Michigan)
- Harrison Craig Chapman (Colorado State University)
- Jie Chen (Tohoku Univ.)
- Sangbum Cho (Hanyang University)
- Tommaso Cremaschi (Boston College)
- Subhadip Dey (UC Davis)
- João Miguel Dias-Ferreira-Nogueira (University of Coimbra)
- Brandy Guntel Doleshal (Sam Houston State University)
- Chaya Rochel Flint (Columbia University)
- Kei Funano (Tohoku University)
- Robert Cyrus Haraway-III (Oklahoma State University)
- Eriko Hironaka (Florida State University)
- Neil Reardon Hoffman (Oklahoma State University)
- Young Sik Huh (Hanyang University)
- Tejas Deepak Kalelkar (Indian Institute of Science Education and Research Pune)
- Tamas Kalman (Tokyo Institute of Technology)
- Charles Walter Katerba (Montana State University)
- Mokoto Kato (University of Tokyo)
- Kyeongro Kim (KAIST)
- Takahiro Kitayama (The University of Tokyo)
- Yuya Koda (Hiroshima University)
- Alice Na Kwon (CUNY Graduate Center)
- Christine Ruey Shan Lee (University of Texas at Austin)
- Vincent Frederick Longo (University of Nebraska-Lincoln)
- Bruno Martelli (Università di Pisa)
- Hidetoshi Masai (Tohoku University)
- Maggie Hall Miller (Princeton University)
- Christian R Millichap (Linfield College)
- Sujoy Mukherjee (The George Washington University)
- Shawn Thomas Rafalski (Fairfield University)
- Nozomu Sekino (The university of Tokyo)
- Koya Shimokawa (Saitama University)
- Hyunshik Shin (KAIST)
- Alexander James Stas (CUNY Graduate Center)
- Lijie Sun (Tokyo Institute of Technology)
- Masaaki Suzuki (Meiji University)
- Kazuto Takao (Kyoto University)
- Katherine Elena Tucker (University of Nebraska-Lincoln)
- Marla Joy Williams (University of Nebraska-Lincoln)
- Zhongtao Wu (The Chinese University of Hong Kong)
- Yang Xiao (Brown University)
- Mohammadmahdi Yazdi (University of Oxford)
7. Other
Nothing to report.



