"3-manifolds in trisections" by Dr. Dale Koenig
Date
Location
Description
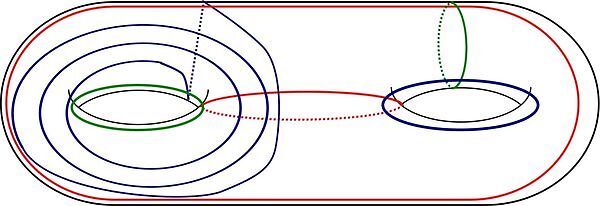
A trisection of a 4-manifold is determined by a 3-dimensional singular subset called the spine. The spine is in turn determined by 3 cut systems on a surface. We search for 3-manifolds embedded in the 4-manifold such that the 3-manifold lies "almost" in the spine. Often these 3-manifolds can be seen directly in diagrams for the trisection. We apply these findings to prove results about embedding 3-manifolds in connect sums of sphere bundles without reference to trisections. In particular, we can calculate upper bounds on the smallest number k for which the 3-manifold embeds in a connect sum of k copies of sphere bundles over a sphere.
Subscribe to the OIST Calendar: Right-click to download, then open in your calendar application.



