Past Events
Colloquium: "Fiber bundle and gauge theory" by Mr. Ryusei Maeda
2020年2月21日 (金) 10:00 〜 12:00Speaker: Mr. Ryusei Maeda is a 3rd year undergratuate student at University of Tokyo and is currently visiting OIST as a research intern.
Colloquium: "Maxwell's equations, Yang-Mills equations and differential forms" by Mr. Ryusei Maeda
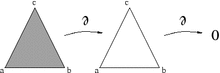
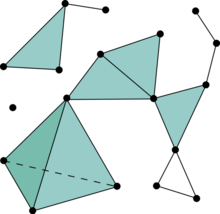
2020年2月14日 (金) 10:00 〜 12:00Colloquium: "Simplicial homology, part II" by Dr. Guilherme Sadovski
2020年2月13日 (木) 14:00 〜 16:00Speaker: Dr. Sadovski is a member of this unit (visit his page)
Colloquium: "Simplicial homology, part I" by Dr. Guilherme Sadovski
2020年2月10日 (月) 10:00 〜 12:00Speaker: Dr. Sadovski is a member of this unit (visit his page)
Minicurse: Morse Theory
2020年2月7日 (金) 13:00Speaker: Prof. Andrew Lobb
Morse theory is a branch of mathematics with which we can infer topological information of manifolds. In this series of lectures we will explore its formulation and how it encodes topology.
Colloquium: "Basics of differential geometry and General Relativity" by Mr. Ryusei Maeda
2020年2月7日 (金) 10:00 〜 12:00Speaker: Mr. Ryusei Maeda is a 3rd year undergratuate student at University of Tokyo and is currently visiting OIST as a research intern.
Minicurse: Morse Theory
2020年2月6日 (木) 9:30Speaker: Prof. Andrew Lobb
Morse theory is a branch of mathematics with which we can infer topological information of manifolds. In this series of lectures we will explore its formulation and how it encodes topology.
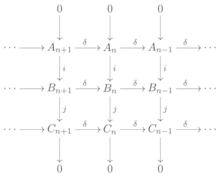
Colloquium: "General homology theory" by Dr. Guilherme Sadovski
2020年2月5日 (水) 10:00 〜 12:00Speaker: Dr. Sadovski is a member of this unit (visit his page)
Coloquium: "Functional methods in QFT and renormalization, part IV" by Dr. Riccardo Martini
2020年1月30日 (木) 14:00In this seminar we introduce the regulator functional that is at the core of the Functional renormalization group and discuss its properties.
Research Intern: Ryusei Maeda
2020年1月30日 (木) (All day) 〜 2020年3月11日 (水) (All day)Research Intern: Ryusei Maeda