FY2013 Annual Report
Collective Interactions Unit
Assistant Professor Mahesh Bandi
Abstract
We are an experimental group with broad interests in soft matter physics, applied mathematics, mechanics, and their application to biologically inspired problems. Our experimental skills, the tools in our labs, and around the OIST campus, allow us to work in the general area that concerns macroscopic, non-relativistic matter and collective phenomena that emerge from their interactions. Our current interests are in problems related to interfacial fluid dynamics, granular solids, and biomechanics of the human foot.
1. Staff
Members (as of March 31, 2014)
- Dr. Mahesh M. Bandi, Assistant Professor
- Dr. Tamoghna Das, Postdoctoral Scholar
- Dr. Aryesh Mukherjee, Postdoctoral Scholar
- Dr. Venkata Sathish Akella, Postdoctoral Scholar
- Dr. Dhiraj Kumar Singh, Postdoctoral Scholar
- Dr. Colm P. Connaughton, Sabbatical Visitor (from Univ. of Warwick, UK)
- Mr. Kenneth Jerome Meacham III, Technical Staff
- Ms. Ayano Sakiyama, Research Administrator
Alumni
- Dr. Ceyda Sanli-Cakir, Postdoctoral Scholar
- Dr. Deniz Cakir, Visiting Researcher
- Dr. Jean-Francois Metayer, Postdoctoral Scholar
- Mr. Mart Toots, Graduate Student (Lab Rotation)
2. Collaborations
- Theme: Waving of Marine Grass
- Type of collaboration: Joint research
- Researchers:
- Mr. Ravi Singh, Brown University, USA
- Professor Shreyas Mandre, Brown University, USA
- Professor L. Mahadevan, Harvard University, USA
- Professor A. Mahadevan, Woods Hole Oceanographic Institution, USA
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Theme: Foot in motion - materials, mechanics & control (funded by HFSP)
- Type of collaboration: Joint research
- Researchers:
- Professor Madhusudhan Venkadesan, National Centre for Biological Sciences, India
- Mr. Nihav Dhawale, National Centre for Biological Sciences, India.
- Ms. Neelima Sharma, National Centre for Biological Sciences, India.
- Professor Shreyas Mandre, Brown University, USA
- Ms. Maria Fernanda Lugo-Bolanos, Brown University, USA
- Dr. Marcelo Dias, Brown University, USA
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Dr. Dhiraj K. Singh, OIST Graduate University, Japan
3. Activities and Findings
3.1 Relating non-equilibrium dynamics with structural transition in two-dimensional aggregates.
We approach this complex problem in a simple setting. We consider a two-dimensional system of mono-disperse particles interacting pairwise via an effective potential consisting of short-range attraction and long-range repulsion and monitor their real-space trajectories using molecular dynamics. Our choice of the model system and method is particularly suitable for the aimed study for the following reasons. Competition between the strength (in arbitrary units) and range (in units of particle diameter) of attraction and repulsion are known to lead to phase separation in particulate systems. Our model system is thus guaranteed to reach a steady non-ergodic state below certain temperature independent of preparation protocol. Note that the preparation history has always added extra complexity in the description of example systems mentioned earlier. Easy and precise tuning of competing energy and length scales provides an opportunity for a comprehensive study of both structures and dynamics. Indeed, this simple system offers a very rich phase diagram comprising structural, geometric and dynamical transitions. Furthermore, simultaneous observation of structure and dynamics offers a promise to connect time- and length-scales which have proved challenging so far.
Model potential
We start by describing the essential features of our model system. We consider a system of N mono-disperse particles of unit mass in a two-dimensional (2D) square geometry with periodic boundary conditions applied to all directions. The particles interact only pair-wise via an effective potential consisting of a short-range attraction and long-range repulsion. The range is always defined in units of particle diameter setting the length scale of the problem. A generalised Lennard-Jones 2n-n form has been chosen to model the short-range attraction. Our choice of n = 18 for the present study ensures an attractive well width of 0.5 times the particle diameter. This choice of n stems from experimental motivation of studying polymer-coated colloidal particles. Moreover, theoretically, it has already been established that the thermodynamic properties of an interacting particles system do not change for n greater than 18. The solvent in which these particles are immersed has been modelled implicitly by a screened-Coulomb or Yukawa interaction. The long-range repulsive feature of Yukawa interaction is governed by its strength (in energy units) and screening length (in particle diameter units). As we set the repulsion to attraction strength ratio to unity, the screening length is the sole tuning parameter for the effective interaction. Before charting out our findings as a function of screening length, we describe the method for preparation of the system in the next section.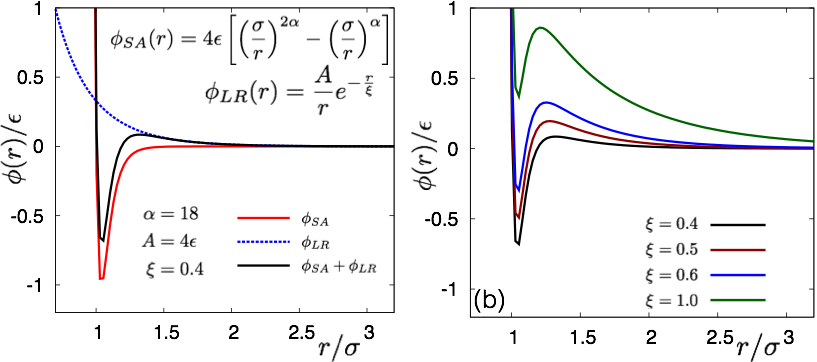
Fig.1 Functional form of the effective pair-potential has been plotted together with its short-attraction and long-repulsion part for specific parameter values indicated in (a). Note that the global minimum of the effective potential is followed by a positive energy barrier at finite distance from particle core. Increase in the energy barrier as a function increasing repulsion length is shown in (b).
Simulation details
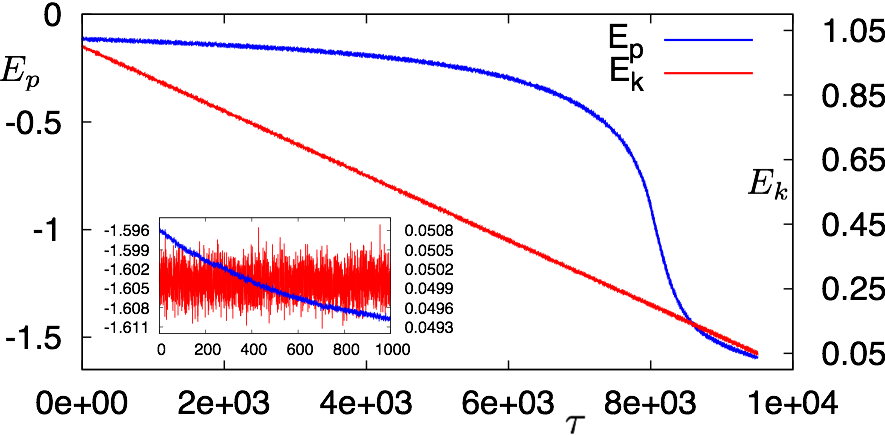
We employ traditional molecular dynamics with velocity Verlet scheme to simulate our model system in canonical constant number-area-temperature (NAT) ensemble. We start with a system of unit density in a square box of size 400 x 400. As mentioned earlier, periodic boundary conditions are applied in both directions of the 2D box. Particles are then randomly eliminated from the box to reach the desired density. Most of the results presented here are for a system of density 0.4 which consists of 64,000 particles.The system is initialised and equilibrated at temperature T = 1.0 where the temperature is measured in energy units and the Boltzmann constant has been set to unity. To keep the temperature constant, a Langevin thermostat has been used which also takes care of the dissipative nature of the implicit solvent. The time step for the integration of the equation of motion is set to 10^(-3) throughout the simulation. Once equilibration is achieved, the temperature is linearly ramped down to a much smaller final temperature Tf = 0.05 over four decades of time (10^7 time steps). The final temperature is then held constant over three decades of time (10^6 time steps) and finally configurations for further analysis has been stored in an interval of 100 time steps.
Fig.2 Evolution of potential energy per particle (left Y-axis) and bulk temperature (right Y-axis) have been plotted against simulation time during the slow cooling down of our model system described in the text. During linear ramp-down of bulk temperature, potential energy per particle shows abrupt decay at a temperature which coincides with the liquid-gas critical temperature of bare attraction potential considered.This observation is independent of the repulsion length used in our simulation. After reaching desired temperature T = 0.05 by cooling temperature is held fixed as shown in inset, however, the potential energy continues to decay within the observation time indicating the non-equilibrium state of the system.
Non-ergodicity from very slow cooling !
During the cooling process, the potential energy per particle Ep for the model system shows a very slow linear decay up to certain temperature Tc ~ 0.25, below which it drops sharply and never settles around a steady mean value. This observation holds irrespective of the repulsive screening length and indicates the system to go out of equilibrium. We note that this particular value coincides with the gas-liquid critical temperature reported for an interacting system with bare attraction. We have confirmed this observation by employing a step-wise quasi-static cooling protocol. The robustness of this observation prompts us to state that the inherent frustration due competing length scales sets in the system as entropic contribution becomes smaller at low temperature and manifests into non-ergodicity. However, the high temperature thermodynamics of the model system is solely governed by the attractive part. Following up the very slow cooling process, Ep never settles down within our observation time when a constant temperature is maintained with a standard deviation of the order of 10^(-3). A stretched exponential decay of Ep has been observed over this time which is again a characteristic of non-equilibrium relaxation. We shall provide further evidence of non-ergodicity in later sections.
Observing non-ergodicity in a system with competing interactions is not entirely unexpected as the same due to phase-separation has long been predicted by Lebowitz and Penrose in 1966. Since then, similar phenomena have been observed in diverse systems ranging from pasta phases at the core of neutron star to DNA self-assembly including the aggregation of quantum dots, nano particles and coated colloids. The novelty of our finding lies in the fact that we show even a very slow cooling is enough to drive the system out of equilibrium and thus confirms the process to be independent of preparation history. Note that the same was achieved in all the previous examples through a history dependent driving protocol which made the understanding of final states difficult. We hope that our results will provide a firm intuitive basis for the understanding of other history-dependent non-equilibrium processes like glass transition.
Inherent structures
As non-equilibrium systems are always associated to metastable energy minima, the natural question to ask next is what is the possible lowest energy configuration for our model system? We use numerical energy minimisation to investigate this question. We choose the last configuration from the constant temperature run at final temperature and minimise the total configurational energy using steepest decent method to find the inherent structures. This method, of course, does not ensure a global minimisation. It is justified to state that the final configuration resulted from this minimisation correspond to a local minimum defined by the force tolerance of 10^(-8). The minimised configurations show a clear structural transition evident from a simple visual inspection. For repulsion length below 0.5, the inherent structure consists of disconnected crystalline patches with local hexagonal order. These compact structures become more and more string-like or non-compact as the screening length goes beyond 0.5. Noting that the attractive well width for our specific choice of n is 0.5, it is evident that the competition between length scales is responsible for the structural transition. Further observational support of this transition can be found in terms of energetics of these configurations. The minimised total energy per particle increases non-linearly as the repulsion length increases to 0.5 and becomes linear after.

Fig.3 The potential energy perparticle of the inherent structure (described in text) is plotted as a function of repulsion length (a). Please note the functional change when the repulsion length equals attraction well width. Choosing this repulsion length as a reference, we plot the particle configurations of obtained inherent structures (b) below, (c) at and (d) above the refernce value at fixed density and temperature. A compact to non-compact structural transition of aggregates is evident from visual inspection itself.
It is tempting to assume an effective three-body interaction to be responsible for such development of anisotropy in a system of particles interacting via pair-wise centro-symmetric potential. To this end, we have calculated simple three-body interaction energy as a function of repulsion length as follows. A pair of particles has been fixed at the distance of minimum potential energy from each other. Now a third particle has been introduced at a length of minimum pair distance form either or both of the fixed particles. The triangular structure preserving hexagonal symmetry has always been the minimum energy configuration for all values of repulsion length. This observation clearly goes against the assumption of three-body interaction. More detailed explanation in this line shall require detailed investigation which we leave for future. In the next sections we shall focus on the properties of finite temperature configurations.
Characterisation of structural transition at finite temperature
First thing we note about the finite temperature (Tf = 0.05) configurations is their remarkable statistical semblance with the corresponding inherent structures. The structural transition observed in the inherent structures survives under thermal fluctuations. This ensures that our very slow cooling protocol has fetched the system at least close to some local minima while maintaining the non-equilibrium characteristic. Below we present the statistical characterisation of the local structures and discuss how that changes as a function of repulsive screening length. All the results presented afterwards are for density 0.4 unless stated otherwise.
Static pair correlation function is the first quantity that we study systematically. This correlation quantifies the expectation of finding a particle at a certain distance from one arbitrarily chosen central particle and provides information about microscopic structural arrangement in a angle-averaged way around the central particle. The first prominent peak at a pair distance close to but greater that unity is due to the particles in the nearest neighbour shell of the central one. The split second peak of this function indicates strong structural correlation in the second nearest neighbour shell rather than a random liquid-like arrangement expected at this low density. This can only happen due to particle aggregation. The split peaks go from symmetric to asymmetric as a function of repulsion length following the structural transition described earlier.
This observation can further be understood with the following mental picture of local particle arrangements. Consider such a triad of particles where each of the particles are positioned at the potential energy minimum of any two other particles. The X-axis is assumed to pass though the centre of mass of this triad located at the origin. A fourth particle can be introduced only at the integer multiples of pi/3 to satisfy the preferred hexagonal symmetry in two-dimensions. When the repulsion length is smaller than the attraction well width, this situation is holds leading to the patches of local crystalline order. However, as soon as the repulsion length becomes larger, this angular preference is lifted and the fourth particle can join the triad at arbitrary angles resulting into non-compact structures.
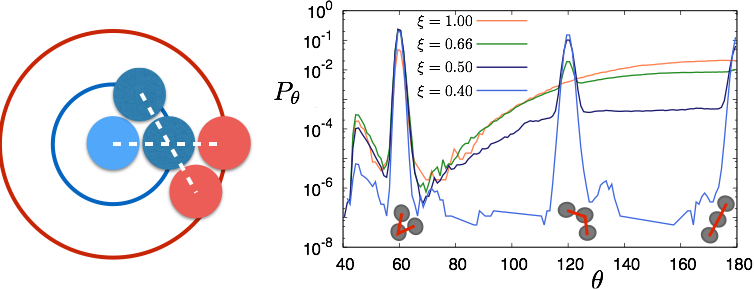
Fig.4 Possible three-body arrangements in an ideal triangular lattice has been shown on left as a cartoon. The distribution of possible three-body angles calculated using finite temperaure configurations are plotted next to it. Please note that the distinct peaks at 2pi/3 and pi for low repulsion length goes away as the repulsion length increases.
We verify this picture by explicitly calculating the distribution of three-body angles using our simulated configurations. The three-body angle is the angle between any two pairs of particles forming a triad where each of the particles is the nearest neighbour of two others. We focus on the obtuse part of the angle distribution as the acute part shall always have only one distinct peak at pi/3 due to the preferred triangular geometry in two-dimensions. The obtuse part of the distribution indeed shows two distinct peaks at angles 2pi/3 and pi for repulsion length smaller than 0.5 which is the width of attraction well. These two peaks are indicative of the two preferred position of neighbours in the second shell described in the previous paragraph. As repulsion length increases the height of these peaks (at 2pi/3 and pi) becomes smaller and probability of other three-body angles become positive. When repulsion length is much larger than 0.5, the distribution grows monotonically from smaller obtuse values to pi. The maximum at pi is expected as the configurations now consist of linear string-like aggregates.
For further quantification of shape, the statistics of radius of gyration for the aggregates has been studied. The scaling relation between the radius of gyration of a cluster of particles and the number of constituent particles is a well known measure for the shape of the cluster. Two limits are important here. The scaling exponent 2 refers to a circular structure which is the most compact form possible in two-dimensions. The exponent is 1 while the structure is strictly linear. For our simulated aggregates this exponent varies between these two limits as a function of repulsion length. The radius of gyration of a cluster while plotted against its size in the log-log scale shows a change in slope from less than 2 to greater than 1 as repulsion length goes from smaller to larger with respect to the width of attraction well. The clusters corresponding to the intermediate values of slope around 1.5 are of fractal nature while the repulsion and attraction length scales balance each other.
Geometric transition as a function of density
We shall conclude our discussion about the static structures with a description of the effect of increasing density on it. All the results presented so far are for a system of low density 0.4. As the number density is increased by eliminating less number of particles from our initial system of unit density, the cluster size increases as expected. At certain density 0.5, a percolated cluster appears spanning the whole system. This transition is of purely geometric origin and can be identified clearly from the cluster size distribution. The distribution is always exponential for densities smaller than 0.5 and becomes algebraic at density 0.5. The exponent for the decay of scale-free cluster size is close to that of random percolation. This observation is robust as is independent of repulsion length. However, we note that the complex interplay between the strength of attraction and repulsion taken together with the variation of attraction well can change this scenario considerably. These percolated structures are formally identified as gels. The local structures of these gels are still dependent on the repulsion length though. We set aside any further characterisation of these gel states for future correspondence. In the next section, we shall discuss the dynamical properties of low density aggregates and argue for the possible interconnection between the dynamical properties and structural transition.
Conclusion
We present a molecular dynamics study of a two-dimensional particulate system interacting pairwise via competition between short-range attraction and long-range repulsion. For a certain low density and temperature, we chart out the structural and dynamical features as a function of the repulsive screening length while keeping the attraction length scale fixed and equating the strength of attraction and repulsion. Despite these restrictions, we find that the competition between the length scales alone guides the system to non-ergodicity through a very slow cooling process eliminating any dependence on preparation history. Being in a non-equilibrium steady state, our model system shows a structural transition from compact to non-compact even while the interaction is radially symmetric. A purely geometrical transition has also been observed as an increasing function of density where the local structures are still governed by repulsion length.
We are currently working towards a more complete view of the parameter space and attempting to complete the findings using scaling arguments. In particular, we expect, the dynamics of the system will share features common to out-of-equilibrium systems, such as intermediate time relaxation, long time sub-diffusion and non-Gaussian feature of self-displacement fluctuation. We also hope to further associate the dynamical features with morphology. While the merit of the present work is exploratory at this stage, we hope that it will provide a synthesis of a wide range of parameter space relevant for the system. We hope these results can be used as leitmotifs for further detailed understanding of diverse systems driven out of equilibrium.
3.2 Surfactant-driven fracture of two-dimensional solids

4. Publications
4.1 Journals
- Bandi, M. M., Concha, A., Wood, R. & Mahadevan, L. A pendulum in a flowing soap film. Physics of Fluids 25, 041702, doi:http://dx.doi.org/10.1063/1.4800057 (2013).
- Bandi, M. M., Rivera, M. K., Krzakala, F. & Ecke, R. E. Fragility and hysteretic creep in frictional granular jamming. Physical Review E87, 042205(042214), doi:10.1103/PhysRevE.87.042205 (2013).
4.2 Books and Other One-Time Publications
None to report
4.3 Oral and Poster Presentations
- Bandi, M. M. Table-top experiments in carbon geo-sequestration, in Fluids Seminar, Department of Mechanical & Aerospace Engineering, Seoul National University (2013). [Invited Oral Presentation]
- Bandi, M. M. Cooperative strategies in fungal spore dispersal, in 7th International Congress on Biomimetic, Artificial Muscles & Nano-Bio, Jeju Island (2013). [Invited Oral Presentation]
- Bandi, M. M. Fragility and hysteretic creep in frictional granular jamming, in Statphys 25 Conference, Seoul National University (2013). [Contributed Poster Presentation]
- Bandi, M. M. Fragility and Hysteresis in Frictional Granular Jamming, in The 18th International Conference on Nonlinear Elasticity in Materials, Ascona, Canton Ticino, Switzerland (2013). [Invited Oral Presentation]
- Bandi, M. M. Fragility and Hysteresis in Frictional Granular Jamming, in Complex Dynamics in Granular Systems, Kavli Institute for Theoretical Physics China at the Chinese Academy of Sciences (2013). [Invited Oral Presentation]
- Bandi, M. M., Tallinen, T. & Mahadevan, L. Shock-driven jamming and periodic fracture at particulate interfaces, in Complex Dynamics in Granular Systems, Kavli Institute for Theoretical Physics China at the Chinese Academy of Sciences (2013). [Invited Oral Presentation]
- Das, T. & Bandi, M. M. Equilibrium and non-equilibrium aggregation in two dimensional systems with competing interactions, in APS March Meeting 2014, Convention Center, Denver, Colorado, USA (2014). [Contributed Oral Presentation]
- Singh, R. S., Mandre, S., Mahadevan, A., Mahadevan, L. & Bandi, M. M. Stability theory for the synchronized waving of marine grass in 66th Annual Meeting of the APS Division of Fluid Dynamics Conference David L. Lawrence Convention Center, Pittsburgh, Pennsylvania, USA (2013). [Contributed Oral Presentation]
- Das, T., Sengupta, S. & Rao, M. Non-affine deformation in a sheared crystal and a hidden elastic critical point, in Statphys25, Seoul National University (2013). [Contributed Poster Presentation]
- Metayer, J.-F. A local view on sheared granular matter, in STATPHYS25, Seoul National University (2013). [Contributed Oral Presentation]
- Bandi, M. M. Cooperative strategies in fungal spore dispersal, Biology Colloquium, Indian Institute for Science Education & Research, Thiruvananthapuram, India (2013). [Invited Oral Presentation]
- Bandi, M. M. Two dimensional particulate systems with competing interactions, Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico, USA (2014). [Invited Oral Presentation]
- Das, T. Equilibrium and non-equilibrium aggregation in two-dimensional systems with competing interactions, Indian Association of the Cultivation of Science, Kolkata, India (2013). [Invited Oral Presentation]
- Das, T. Equilibrium and non-equilibrium aggregation in two-dimensional systems with competing interactions, Dept.of Physics, Ramakrishna Mission Vivekananda University, Kolkata, India (2014). [Invited Oral Presentation]
5. Intellectual Property Rights and Other Specific Achievements
5.1 Intellectual Property
None to report
5.2 External Grants
- Grant Title: Foot in Motion: Materials, Mechanics & Control
- Funding Agency: Human Frontier Science Program, Strasbourg, France
- Funding: USD 350,000 per year (Sept 2013 - Aug 2016)
- Collaborators:
- Professor Madhusudhan Venkadesan, National Centre for Biological Sciences, India (PI)
- Professor Shreyas Mandre, Brown University, USA (Co-PI)
- Professor Mahesh M. Bandi, OIST Graduate University, Japan (Co-PI)
6. Meetings and Events
6.1 Seminar
-
Date: May 14, 2013
-
Venue: OIST, C209
-
Speaker: Mr. Francois Ingremeau
-
Équipe instabilités et turbulence LOMA, CNRS université Bordeaux1, France
-
Date: September 17, 2013
-
Venue: OIST, C210
-
Speakers: Associate Professor Hiroaki Katsuragi, Mr. Naoki Iikawa
-
Department of Earth and Environmental Sciences, Nagoya University, Japan
-
Date: October 8, 2013
-
Venue: OIST, C210
-
Speaker: Dr. Avadh B. Saxena
-
Los Alamos National Laboratory, USA
-
Date: February 14, 2014
-
Venue: OIST, B503
-
Speaker: Assistant Professor Golan Bel
-
Ben-Gurion University of the Negev, Israel
-
Date: February 17, 2014
-
Venue: OIST, B503
-
Speaker: Mr. Saikat Basu
-
Department of Engineering Science and Mechanics, Virginia Polytechnic Institute and State University, USA
-
Date: March 11, 2014
-
Venue: OIST C016
-
Speaker: Professor Hisao Hayakawa
-
Yukawa Institute for Theoretical Physics, Kyoto University, Japan
7. Others
None to report.