FY2022 Annual Report

Neural Coding and Brain Computing Unit
Professor Tomoki Fukai

Abstract

This unit has been exploring the brain's neural mechanisms underlying cognitive functions, especially learning and memory. We are interested in clarifying how neural networks in the brain integrate single-cell computation such as dendritic computation with network-level computation to generate higher cognitive functions. In recent years, we focussed on how the brain segments potentially important pieces of information from continuous streams of sensory input. We will use our findings for modeling the brain mechanisms of not only memory processing but also inference and language processing.
 

1. Staff

  • Staff Scientist
    • Tatsuya Haga, PhD
  • Postdoctoral Scholar
    • Ibrahim Alsolami, PhD
    • Milena Menezes Carvalho, PhD
    • Daniel Müller-Komorowska, PhD
  • Ph.D. Student
    • Thomas Burns
    • Gaston Sivori
    • Maria Astrakhan
    • Roman Koshkin
    • Munenori Takaku
    • Hugo Musset
    • Balashwethan Chockalingam
  • Rotation Student
    • Ryo Nakatani (Term 3)
    • Timofei Kargin (Term 1)
    • Sandeep Vijayan (Term 2)
    • Yusaku Kasai (Term 2)
  • Research Intern
    • Yuta Konno (Jan-Apr 2022)
    • Yaroslav Korobov (May 2022-Apr 2023)
    • Tom George (May-Aug 2022)
    • Kotaro Muramatsu (Jun-Sep 2022)
    • Dmitriy Sakharuk (Oct 2022-Apr 2023)
    • Naima Elosegui Borras (Oct 2022-Mar 2023)
  • Research Unit Administrator
    • Kiyoko Yamada

2. Collaborations

2.1 "Idling Brain" project

         kaken.nii.ac.jp/en/grant/KAKENHI-PROJECT-18H05213

  • Supported by Grant-in-Aid for Specially Promoted Research (KAKENHI)
  • Type of collaboration: Joint research
  • Researchers:
    • Professor Kaoru Inokuchi, University of Toyama
    • Dr. Khaled Ghandour, University of Toyama
    • Dr. Noriaki Ohkawa, University of Toyama
    • Dr. Masanori Nomoto, University of Toyama

2.2 Chunking sensorimotor sequences in human EEG data

  • Type of collaboration: Joint research
  • Researchers:
    • Professor Keiichi Kitajo, National Institute for Physiological Sciences
    • Dr. Yoshiyuki Kashiwase, OMRON Co. Ltd.
    • Dr. Shunsuke Takagi, OMRON Co. Ltd.
    • Dr. Masanori Hashikaze, OMRON Co. Ltd.

2.3 Cell assembly analysis in the songbird brain

  • Type of collaboration: Internal joint research
  • Researchers:
    • Professor Yoko Yazaki-Sugiyama, OIST
    • Dr. Jelena Katic, OIST

2.4 A novel mathematical approach to partially observable Markov decision processes

  • Type of collaboration: Joint research
  • Researchers:
    • Haruki Takahashi, PhD student, Kogakuin University
    • Prof. Takashi Takekawa, Kogakuin University
    • Prof. Yutaka Sakai, Tamagawa University

3. Activities and Findings

3.1 Modeling blind source separation in the human auditory system

We used a single-cell model for chunking (Asabuki and Fukai, Nat Comm 2020) to construct a minimal model of the human auditory system and compared the performance of the model with that of human subjects in auditory segmentation tasks (Dellaferrera et al., Front Neurosci, 2022). Though some deviations were found in the model behavior, the overall segregation capabilities of our model were reminiscent of the features of human performance in various experimental settings involving synthesized sounds with naturalistic properties.

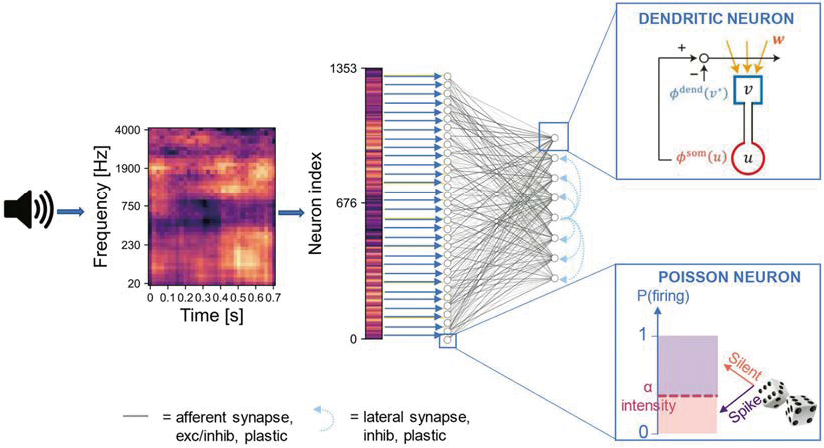
Network architecture for blind source separation. The input signal is pre-processed into a two-dimensional image (i.e., the spectrogram) with values normalized in the range [0,1]. The image is flattened into a one-dimensional array where the intensity of each element is proportional to the Poisson firing probability of the associated input neuron. The neurons in the input layer are connected to those in the output layer through either full connectivity or random connectivity with a connection probability of 30%.

3.2 Chunking complex sequences in gated recurrent neural networks (GRNNs)

Our single-cell model with dendrites could solve the variety of temporal feature analyses. However, some segmentation tasks, including context-dependent segmentation, were difficult for this model. To overcome the difficulties, we developed gated recurrent network models (GRNN) to extend the proposed learning rule to more complex, context-dependent segmentation tasks (Asabuki and Fukai, PLoS Comput Biol, 2022). Recurrent synaptic input multiplicatively regulates the degree of gating current flow from the dendrites to the soma, and we derived an optimal learning rule for afferent and recurrent gating synapses to minimize prediction error (Fig.4). The GRNN combines dendritic computation with a recurrent gating algorithm and dramatically improves the ability of recurrent neural networks to segment complex chunk structures such as mutually overlapping chunks and reverse-ordered chunks. Furthermore, the GRNN successfully detected assemblies of coactivated cortical neurons in large-scale recording data.

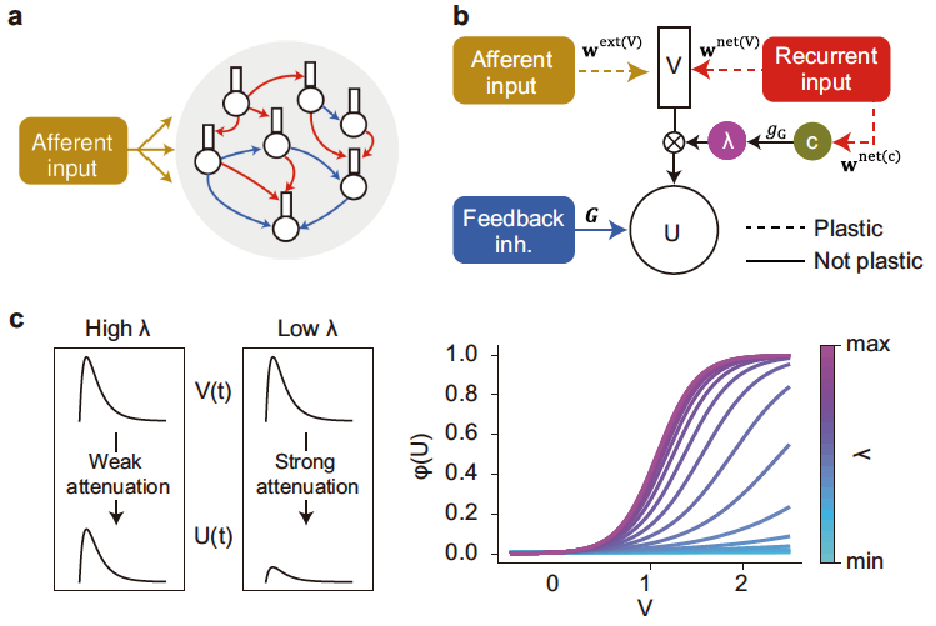
A recurrent gated network of compartmentalized neurons. (a) A network of randomly connected compartmentalized neurons is considered. The red and blue arrows indicate recurrent connections to the dendrite and the feedback inhibition to the soma, respectively. (b) Each neuron model consists of a somatic compartment and a dendritic compartment. Dashed and solid arrows indicate plastic and non-plastic synaptic connections, respectively. Unless otherwise specified, the dendrite only receives afferent inputs. The somatic compartment integrates the dendritic activity and inhibition from other neurons. The gating factor λ is determined by recurrent inputs and regulates the instantaneous fraction of dendritic activity propagated to the soma. (c) The effect of the gating factor on the somatic response is schematically illustrated (left). The relationship between the dendritic potential and somatic firing rate is shown for various values of the gating factor (right).

3.3 Roles of cortical inhibitory circuits for multiscale memory retrieval

Our previous study of associative memory models (Haga and Fukai, PLoS Comput Biol 2021) suggested that the balance between global and local inhibitory connections regulates the spatial scale of segmentation. To test this prediction, we constructed a network model consisting of distinct excitatory and inhibitory neuron pools, proposing an appropriate connection scheme for excitatory neurons and the two inhibitory neuron types (local/global) (Burns et al., eNeuro, 2022). By numerically simulating the model to show that the inhibitory mechanism proposed using the formal model also works in the biologically more realistic network model. We speculate that the local and global inhibitory neuron subtypes correspond to PV+ and SOM+ cortical interneurons, respectively.

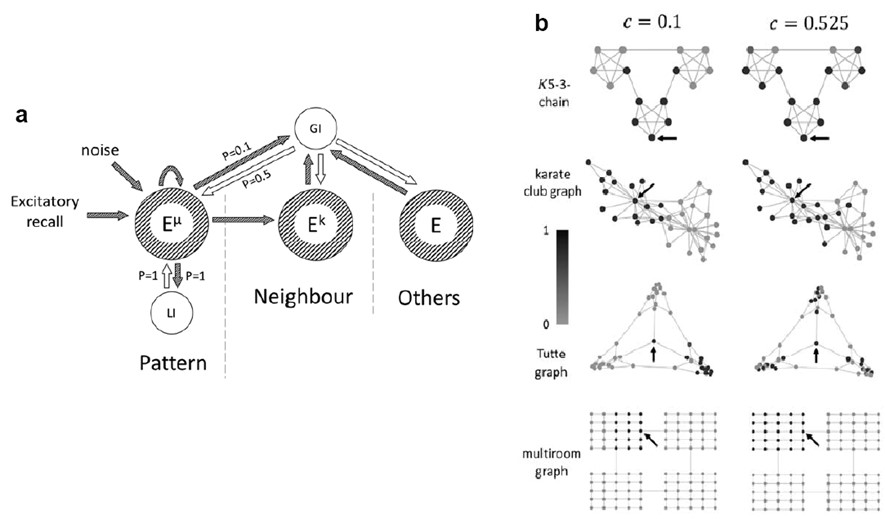
Network model and its segmetation performance. (a) General schematic of the model from the perspective of a single memory pattern (Eμ) and its connections to its respective local inhibitory population (LI), neighbors (Ek), and the global inhibitory population (GI). Connection probabilities are indicated as values of P. To retrieve a pattern, excitation is given directly to a single pattern. Gaussian noise is also applied independently to all excitatory neurons. Striped/shaded arrows and circles indicate excitatory connections and populations, respectively, and unshaded arrows and circles indicate inhibitory connections and populations, respectively. (b) Example trials in the associative memory structures at two values of c. Vertices are shaded according to the sum of neurons’ normalized activity (darker is more active). Arrows indicate the vertex which was stimulated at the beginning of the trial. Each row of subplots in this figure corresponds to data from four different associative memory structures (graphs); from top to bottom: K5-3-chain, karate club graph, Tutte graph, and multiroom graph.

3.4 Role of inhibitory cortical circuits in regulating cortical oscillations

We investigated the effect of the cortical inhibitory circuits on cortical oscillatory dynamics in spontaneous, stimulus-evoked, and attended states (Wagatsuma et al., Cereb Cortex 2022). We numerically explored the regulatory roles of the inhibitory microcircuit in visual information processing by developing a microcircuit model of the visual cortex layers 2/3. We considered the lognormal conductance distribution of excitatory-to-excitatory cortical synapses as this long-tail distribution is known theoretically to exert a strong impact on the dynamical properties of spontaneous cortical activity (Teramae et al., 2012). Simulations of our network model accounted for various experimental findings. In particular, PV+ and SOM+ interneurons are crucial for generating coherent neuronal firing at gamma (30-80 Hz) and beta (20-30 Hz) frequencies, respectively. Furthermore, our model predicted rapid inhibition from VIP to SOM subtypes underlies marked attentional modulation in pyramidal cell responses at slow-gamma frequencies (30-50 Hz). Our results suggest the distinct but cooperative roles of interneuron subtypes in establishing visual perception.

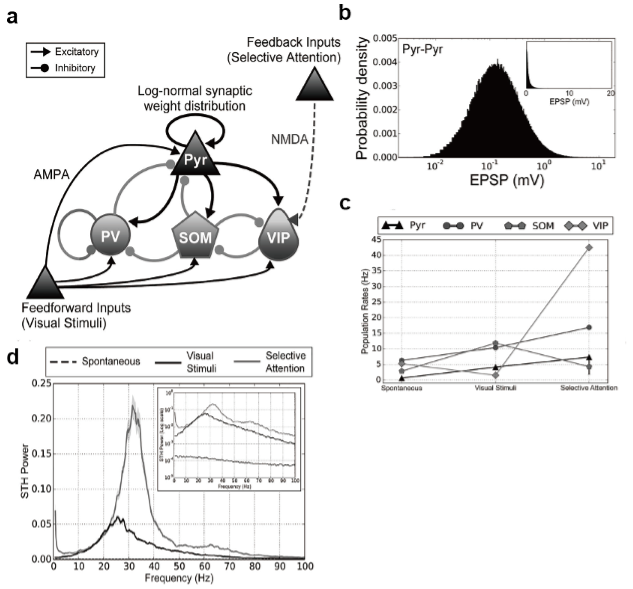
A cortical microcircuit model and its responses. (a) The architecture of the proposed microcircuit model for cortical layers 2/3 of the V1. The microcircuit model consisted of excitatory Pyr neurons and 3 subtypes (PV, SOM, and VIP) of inhibitory interneurons. The neurons used were modeled as integrate-and-fire neurons. Arrows with triangular and circular heads represent excitatory and inhibitory synaptic connections, respectively. Excitatory synaptic connections within this cortical microcircuit network and feedforward inputs (visual stimuli) are driven by AMPA receptors, whereas feedback signals (selective attention) rely on NMDA receptors. (b) Excitatory synaptic weights between Pyr neurons were distributed according to a log-normal distribution. Other synapses obeyed Gaussian distributions. (c) c) The mean population firing rates of Pyr (triangles), PV(circles), SOM (pentagons), and VIP (squares) neurons were calculated over 50 simulation trials of the spontaneous, visual stimulus, and selective attention conditions. Error bars indicate SEs. d) Spike time histogram (STH) power of Pyr neurons, averaged over 50 simulation trials in the spontaneous (black dashed), visual stimulus (black solid), and selective attention (gray solid) conditions. The inset shows a log-scale plot of the same STH power results. The shading of the curves indicates the SE of the mean from 50 simulation trials.

3.5 Partially synchronous states in coupled oscillators

We numerically and analytically studied chimera states in a coupled network of Stuart-Landau oscillators (Bi and Fukai, Chaos, 2022). Chimera states have recently been a hot topic of experimental and theoretical studies. These studies are interesting in neuroscience because coherent and incoherent subsystems coexist in these states through symmetry breaking. Previous theoretical studies focused on either pure phase or pure amplitude-type chimera states, but the interactions between the two degrees of freedom have attracted little attention. We showed two types of amplitude-mediated chimera states and sequential phase transitions connecting them. The first type, i.e., intermittent amplitude-mediated chimera states, is characterized by multicluster chimera states displaying turbulent behavior. The second type, i.e., stationary amplitude-mediated chimera states, shows periodically changing amplitudes across oscillators in both coherent and incoherent subgroups. Though the Stuart-Landau oscillator system is far from biological, it allows an analytic study of the phase transition phenomena between various chimera and non-chimera states. Our results demonstrated how the oscillation amplitude interacts with the phase degrees of freedom in chimera states to generate complex sequences of phase transitions among these states andwill open a window to study the novel kind of chimera states.

Two types of chimera states in the strong coupling regime. Stuart-Landau oscillators were arranged on a ring labeled by a continuous variable x. Snapshots of the stationary states were obtained for the original model with the system size N = 512. (a) The spatial profiles of the phase θ(x) (black) and amplitude |W(x)| (blue: multiplied by 9) in an intermittent amplitude-mediated chimera state. (b) Spatiotemporal evolution of the intermittent amplitude-mediated chimera states. (c) and (d) Similar quantities in stationary amplitude-mediated chimera states.

3.6 Simplicial Hopfield networks

Pairwise connections have been the most popular connection scheme in the computational neuroscience of memory since it supports attractor dynamics crucial for memory retrieval and look biologically reasonable. Theoretically, however, a question arises about whether we can find a more efficient connection scheme for memory processing by neural networks. Inspired by setwise connectivity in biology, we extend Hopfield associative memory networks by adding setwise connections and embedding these connections in a simplicial complex (Burns and Fukai, International Conference on Learning Representations 2023). Simplicial complexes are higher dimensional analogs of graphs that naturally represent collections of pairwise and setwise relationships. Our simplicial Hopfield networks increased storage capacity for memory patterns sampled from large-scale datasets. Surprisingly, even when connections were limited to a small random subset of equivalent size to an all-pairwise network, our networks still outperformed their pairwise counterparts. We also tested analogous modern continuous Hopfield networks, offering a potentially promising avenue for improving the attention mechanism in Transformer models. Our work demonstrates the computational affordances of group connectivity in memory function, offering new understandings of these fascinating biological mechanisms. The work has been accepted for presentation at the top conference in artificial intelligence.

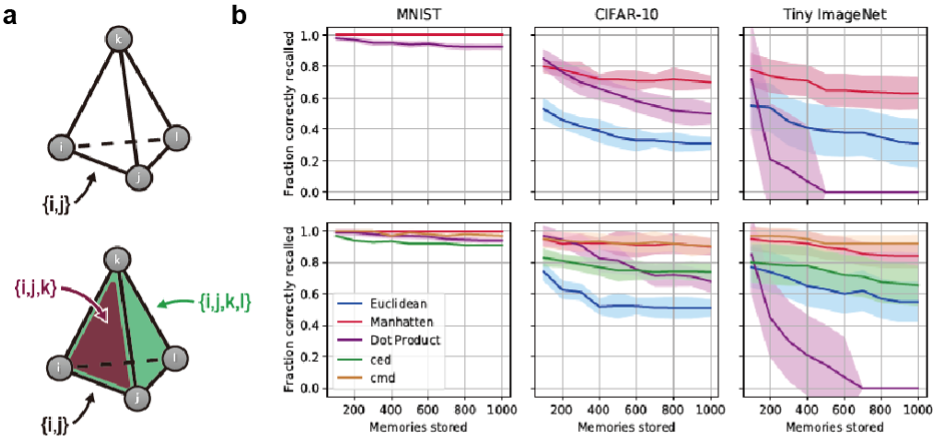
Improved performance of simplicial Hopfield networks. Comparative illustrations of connections in a pairwise Hopfield network (top) and a simplicial Hopfield network (bottom) with network size N = 4. In a simplicial Hopfield network, σ = {i, j} is an edge (1–simplex), σ = {i, j, k} is a triangle (2–simplex), σ = {i, j, k, l} is a tetrahedron (3–simplex), and so on. (b) Recall (mean ± S.D. over 10 trials) as a function of memory loading using the MNIST, CIFAR-10, and Tiny ImageNet datasets, using different distance functions. Here we compare the performance of modern continuous pairwise networks (top row) and modern continuous simplicial networks (bottom row). The simplicial networks are R12 (75%), which mixes 1-simplices and 2-simplices at 25 and 75% ratios. R12 (75%) significantly outperforms the pairwise network at all tested levels where there was no perfect recall (one-way t-tests p < 10−9, F > 16.01). At all memory loadings, a one-way ANOVA showed significant variance between the networks (p < 10−5, F > 11.95).

4. Publications

4.1 Journals

  1. Thomas Burns and Tomoki Fukai (2023) Simplicial Hopfield networks. International Conference on Learning Representations.
  2. Tomoki Fukai (2022) Computational models of Idling brain activity for memory processing (review article). In Specia issue "Idling Brain", Neurosci Res. 2022 Dec 30:S0168-0102(22)00325-X. DOI: 10.1016/j.neures.2022.12.024.
  3. Nobuhiko Wagatsuma, Sou Nobukawa and Tomoki Fukai (2022) A microcircuit model involving parvalbumin, somatostatin, and vasoactive intestinal polypeptide inhibitory interneurons for the modulation of neuronal oscillation during visual processing. Cerebral Cortex, bhac355, DOI: https://doi.org/10.1093/cercor/bhac355
  4. Hongjie Bi and Tomoki Fukai (2022) Amplitude-mediated chimera states in nonlocally coupled Stuart-Landau oscillators. Chaos, 32, 083125, DOI: https://doi.org/10.1063/5.0096284
  5. Toshitake Asabuki, Prajakta Kokate, and Tomoki Fukai (2022) Neural circuit mechanisms of hierarchical sequence learning tested on large-scale recording data. PLoS Comput Biol 18, e1010214. DOI: https://doi.org/10.1371/journal.pcbi.1010214
  6. Thomas F Burns, Tatsuya Haga and Tomoki Fukai (2022) Multiscale and extended retrieval of associative memory structures in a cortical model of local-global inhibition balance. eNeuro, 10.1523/ENEURO.0023-22.2022. DOI: https://doi.org/10.1523/ENEURO.0023-22.2022
  7. Giorgia Dellaferrera, Toshitake Asabuki and Tomoki Fukai (2022) Modeling the Repetition-based Recovering of Acoustic and Visual Sources with Dendritic Neurons. Front Neurosci, 16, 855753. DOI: https://doi.org/10.3389/fnins.2022.855753

4.2 Books and other one-time publications

  1. Tomoki Fukai (2022) デジタルトランスフォーメーションで変わる医療 情報処理機械としての脳とAI (Japanese). PHARM TECH JAPAN 2022年4月号 (Vol.38 No.6)

4.3 Oral and Poster Presentations

Oral Presentations (*invited)

  1. Thomas Burns and Tomoki Fukai. Simplicial Hopfield networks. Neuromatch Conference 2022 (online) (September 27-28, 2022)
  2. Tomoki Fukai. A learning rule for segmenting and modeling probabilistic experiences. Neuromorphic Algorithms 2022 (NEAL2022), Volpriehausen, Germany (September 7, 2022)*
  3. Tomoki Fukai. Neural network modeling for cognitive functions. International Conference on Computer Methods on Cognitome Analysis, Online (Russia) (September 1, 2022)*
  4. Thomas F Burns. Intrinsic topology and geometry of gridworld dynamics, learned representations, and a social place cell hypothesis. International Conference on Computer Methods on Cognitome Analysis, Online (Russia) (September 1, 2022)
  5. Thomas Burns, Tatsuya Haga and Tomoki Fukai. A functional role for inhibitory diversity in associative memory. The 45th Annual Meeting of the Japan Neuroscience Society/NEURO2022 (Okinawa, Japan) (July 2, 2022)
  6. Tatsuya Haga, Yohei Oseki and Tomoki Fukai. 物理空間と意味空間におけるナビゲーションを統合する嗅内皮質の神経表現モデル. The 45th Annual Meeting of the Japan Neuroscience Society/NEURO2022 (Okinawa, Japan) (July 2, 2022)
  7. Munenori Takaku and Tomoki Fukai. ゲート付海馬-前頭葉-視床回路モデルによる空間情報の階層的学習. The 45th Annual Meeting of the Japan Neuroscience Society/NEURO2022 (Okinawa, Japan) (July 1, 2022)
  8. Tomoki Fukai. Neural mechanisms of probabilistic event replays. The Fourth Chinese Computational and Cognitive Neuroscience Conference (CCCN2022), Online (China) (June 24, 2022)*

Poster Presentations

  1. Thomas Burns and Tomoki Fukai. Simplicial recurrent networks for memory and language processing. Society for Neuroscience Annual Meeting, Neuroscience 2022 (San Diego, USA) (November 16, 2022)
  2. Gaston Sivori and Tomoki Fukai.Calcium-based learning rules for the rapid detection of temporal communities in synaptic input. Society for Neuroscience Annual Meeting, Neuroscience 2022 (San Diego, USA) (November 16, 2022)
  3. Roman Koshkin and Tomoki Fukai. Astrocytes facilitate self-organization and remodeling of cell assemblies under STP-coupled STDP. Society for Neuroscience Annual Meeting, Neuroscience 2022 (San Diego, USA) (November 15, 2022)
  4. Toshitake Asabuki and Tomoki Fukai. Spontaneous replay of priors for causal inference in recurrent network models. Society for Neuroscience Annual Meeting, Neuroscience 2022 (San Diego, USA) (November 14, 2022)
  5. Tatsuya Haga, Yohei Oseki and Tomoki Fukai. From grid cells to language: generalized spatial representation model of entorhinal cortex. Society for Neuroscience Annual Meeting, Neuroscience 2022 (San Diego, USA) (November 14, 2022)
  6. Thomas Burns and Robert Tang. Capturing agent braiding in gridworlds can serendipitously detect danger. 9th Heidelberg Laureate Forum (Heidelberg, Germany) (19 September, 2022)
  7. Thomas Burns and Irwansyah. Efficient, probabilistic analysis of combinatorial neural codes with algebraic, topological, and statistical methods. 31st Annual Computational Neuroscience Meeting (Melbourne, Australia) (18 July, 2022)
  8. Thomas Burns, Tatsuya Haga and Tomoki Fukai. Inhibition and associative memory structures. IBRO-RIKEN Summer Program (online) (7 July, 2022)
  9. Thomas Burns and Robert Tang. An example of recasting an AI problem as a geometric one. International Symposium on AI and Brain Science 2022 (Okinawa, Japan) (4-5 July, 2022)
  10. Gaston Sivori and Tomoki Fukai. Self-supervised pattern tuning by somato-dendritic coupling modulation. The 45th Annual Meeting of the Japan Neuroscience Society/NEURO2022 (Okinawa, Japan) (July 2, 2022)

4.4 Seminars

  1. Thomas Burns. Neurons, spaces, and dancing koalas. Centre for Logic and Philosophy of Science, Vrije Universiteit Brussel, Belgium (March 2023).
  2. Thomas Burns. Geometry and topology in memory and navigation. Department of Physiology, Monash University, Australia (January 2023).
  3. Thomas Burns. Algebraic geometry of neural codes. Max Planck Institute for Dynamics & Self-Organization, Gottingen, Germany (October 2022).
  4. Thomas Burns. Cube complexes, curvature, and navigation. Mathematics and Machine Learning Seminar Series, Heidelberg University, Germany (September 2022).
  5. Thomas Burns. Using geometric group theory to study multi-agent navigation. Faculty of Information Technology, Monash University, Australia (July 2022)
  6. Thomas Burns. Associative memory and traumatic brain injury. School of Psychology, Deakin University, Australia (July 2022)
  7. Thomas Burns. Inhibition in memory and disease. Department of Neuroscience, Monash University, Australia (May 2022)

5. Intellectual Property Rights and Other Specific Achievements

5.1 Grants

Kakenhi Grant-in-Aid for Specially Promoted Research

  • Titile: Mechanisms underlying information processing in idling brain
  • Period: FY2018-2022
  • Principal Investigator: Prof. Kaoru Inokuchi (University of Toyama)
  • Co-Investigators: Prof. Tomoki Fukai, Prof. Keizo Takao (University of Toyama)

Kakenhi Graint-in-Aid for Early-Career Scientists

  • Titile: A Comprehensive Theoretical Survey on Functionalities and Properties of Adult Neurogenesis under the Influence of Slow Oscillations
  • Period: FY2019-2022
  • Principal Investigator: Dr. Chi Chung Fung

Kakenhi Graint-in-Aid for Early-Career Scientists

  • Titile: Modeling neural language processing by attractor networks
  • Period: FY2021-2023
  • Principal Investigator: Dr. Tatsuya Haga

Secom Science and Technology Foundation, Grant for Academic meetings and Science and Technology Promotion Project

  • OIST Computational Neuroscience Course 2022 (OCNC2022)

6. Meetings and Events

Nothing to report.

7. Other

  • Thomas Burns. Organising Committee Member, International Conference on Learning Representations (ICLR), Kigali, Rwanda (1 - 5 May, 2023)
  • Tomoki Fukai. Program Committee, NEURO2022 (The 45th Annual Meeting of the Japan Neuroscience Society), Okinawa, Japan (June 30 - July 3, 2022)