FY2014 Annual Report
Collective Interactions Unit
Assistant Professor Mahesh Bandi
Abstract
We are an experimental group with broad interests in soft matter physics, applied mathematics, mechanics, and their application to biologically inspired problems. Our experimental skills, the tools in our labs, and around the OIST campus, allow us to work in the general area that concerns macroscopic, non-relativistic matter and collective phenomena that emerge from their interactions. Our current interests are in problems related to interfacial fluid dynamics, granular solids, biomechanics of the human foot and fluctuations in renewable energy sources.
1. Staff
-
Members (as of March 31, 2015)
- Dr. Mahesh M. Bandi, Assistant Professor
- Dr. Saikat Basu, Postdoctoral Scholar
- Dr. Tamoghna Das, Postdoctoral Scholar
- Dr. Aryesh Mukherjee, Postdoctoral Scholar
- Dr. Venkata Sathish Akella, Postdoctoral Scholar
- Dr. Dhiraj Kumar Singh, Postdoctoral Scholar
- Mr. Ali Yawar, Student Intern
- Mr. Valentin Churavy, Lab Rotation Student
- Mr. Kenneth Jerome Meacham III, Technical Staff
- Ms. Ayano Sakiyama, Research Administrator
2. Collaborations
- Theme: Waving of Marine Grass
- Type of collaboration: Joint research
- Researchers:
- Mr. Ravi Singh, Brown University, USA
- Professor Shreyas Mandre, Brown University, USA
- Professor A. Mahadevan, Woods Hole Oceanographic Institution, USA
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
-
Theme: Foot in motion - materials, mechanics & control (funded by HFSP)
- Type of collaboration: Joint research
- Researchers:
- Professor Madhusudhan Venkadesan, National Centre for Biological Sciences, India
- Mr. Nihav Dhawale, National Centre for Biological Sciences, India.
- Ms. Neelima Sharma, National Centre for Biological Sciences, India.
- Professor Shreyas Mandre, Brown University, USA
- Ms. Maria Fernanda Lugo-Bolanos, Brown University, USA
- Dr. Marcelo Dias, Brown University, USA
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Dr. Dhiraj K. Singh, OIST Graduate University, Japan
- Theme: Compaction in Two-Dimensional Granular Materials
- Type of collaboration: Joint research
- Researchers:
- Professor Hiroaki Katsuragi, School of Environmental Sciences, Nagoya University
- Mr. Naoki Iikawa, School of Environmental Sciences, Nagoya University
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
-
Theme: Hydrodynamics of a self-propelled camphor boat
- Type of collaboration: Joint research
- Researchers:
- Mr. Ravi Singh, Brown University, USA
- Professor Shreyas Mandre, Brown University, USA
- Dr. V. Sathish Akella, OIST Graduate University, Japan
- Dr. Dhiraj K. Singh, OIST Graduate University, Japan
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Theme: Drop impact on a soap film
- Type of collaboration: Joint research
- Researchers:
- Dr. Saikat Basu, OIST Graduate University, Japan
- Mr. Ali Yawar, OIST Graduate University, Japan
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Professor Andres Concha, Adolfo Ibane'z University, Chile
3. Activities and Findings
3.1 Two-dimensional Aggregates
Aggregates are certain non-equilibrium states of matter where constituent units (colloids, nano-particles, proteins, bacteria etc.) assume various patterns with finite range spatial correlation. Structurally they cover the whole range of configurational randomness in between liquids with completely random particle arrangement and completely ordered crystals. Specific patterns are known to result in specific bulk responses useful for varied industrial applications including dynamical control of thermal and electical conductivity, efficient chip designing, trageted drug delivery etc. Furthermore, these systems are ideal candidates to study the interplay between local structure and microscopic dynamics of a system; one of the main theses of condensed matter physics. Beyond asthetic appeal and theoretical importance, such understanding is also crucial for designing new functional materials.
Aggregates formed at interfaces are the main focus of our investigations. Interfacial or two-dimensional aggregates are less explored theoretically and experimentaly in comparison to their three-dimensional counterparts. We have considered a generic model representetive of polymer-coated colloids and globular proteins. The system is two-dimensional where constituent particles are identical and interact pair-wise via an attractive potential. The range of this attraction is only a fraction of the particle diameter. The particles also experience a long-range Yukawa type repulsion resulting from the implicit solvent into which the particles are immersed. The competition between the short-range attraction and long-range repulsion is the key factor underlying the formation of particulate aggregates. The importance of such competing interactions in producing complex patterns was conjectured and theoretically studied in early '60s as a possible extension of van der Waals theory, the most celebrated one in the context of simple liquids. However, such systems could be realised experimentally and studied in detail only recently over the past two decades. A considerable body of literature has been accumulated about different forms of competions in diverse systems mentioned earlier, their specific details, and the resulting patterns. In the present work, we seek a unified, yet simple description for the morphological hierarchy observed in two-dimensions.
At the level of inter-particle interactions, the key factors are the strength and extent of both attraction and repulsion experienced by each particle due to its nearest neighbours. Each of them can be chosen and/or controlled in experiments to certain precision. For example, the strength and range of repulsion can be controlled by changing the salinity and/or pH balance of the medium. The same for attraction depends on the choice of particles and its chemical treatment during synthesis. Different realisation of competition between attraction and repulsion then result into different morphology of aggregates. For strong repulsion, the aggregates are wiggly and string-like (non-compact). As the attraction becomes dominant, the particles arrange themselves in isolated crystalline islands (compact). Percolated structures, known as 'gels', are observed when attraction becomes even stronger. Employing standard tools from liquid states theory, we have been able to encode the details of interactions into two length scales, one each for attraction and repulsion. The ratio of these lengthscales (repulsion over attraction) can now be used as a single parameter to describe the whole hierarchy of observed morphologies. This ratio Λ has a lowest bound of unity where the system can be considered as a set of effective hard disks. Repulsion can be imagined as a soft boundary around these disks. As long as the soft boundary remains 1.5 times the size of hard disks, gels are observed. As repulsion increases, isolated compact structures appear instead of percolated ones. When the soft boundary becomes twice as large as the hard disks, directionality in particle arrangemets starts to appear and string like aggregates are realised.
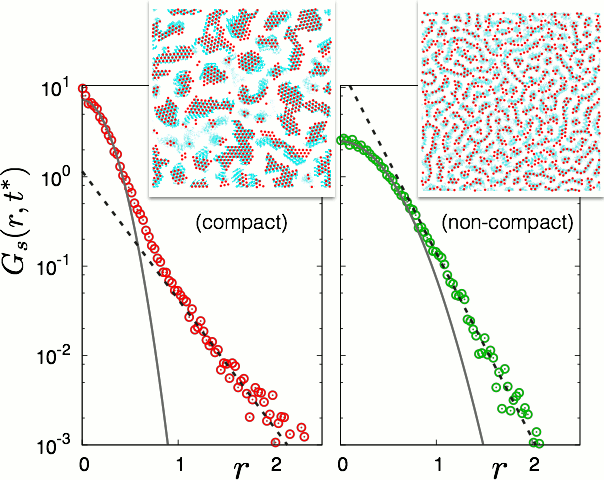
(left panel) Probability of finding a particle at a distance 'r' and time 't=t*' from its position at 'r=0' and 't=0' is plotted for a compact crystalline configuration shown in the inset. As individual particles are always caged by their nearest neighbours, the probability is dominantly Gaussian (within cage) with an exponential tail (escape from cage). In the inset, the red dots represent instantaneous position of particles, say, at time 't*'; the background blue region represent the trajectory of all these particles from 't=0' upto 't*'.
(right panel) The same probability computed for particles in non-compact cluster shown in inset shows completely different behaviour. The distribution is largely exponential with a very small Gaussian near it origin. Directional bonding between particles is responsible for non-compact aggregates.
Standard statistical measures of shape and size of the aggregates are inadequate to characterise and describe the morphological hierarchy of aggregates in full detail. Understanding these structures in terms of configurational randomness turns out to be more useful. An entropic measure based on the static pair correlation function is computed. This measure, known as two-body excess entropy, clearly identifies three distinct morphological classes -- gels or percolated structures, compact crystalline structures and non-compact string-like structures -- when plotted against the dimensionless parameter described in the previous paragraph. Most importantly this result points out a quantitative direct relation between the competing interaction and resulting morphology which can be used to predict the microscopic structure of new materials in future. Another noteworthy result of this work is finding a master relation between the second virial coefficient and Λ the dimensionless descriptor of 2D aggregates. The second virial coefficient quantifies the overall force field experienced by all particles due to all other particles in the system. This is experimentally measurable and has earlier been used successfully to establish the correspondence among simple liquids. The master relation uncovered in the present work shows promise of extending such correspondence to complex liquids with finite spatial correlations. On a practical note, this result can be used to get a grip over the microscopic systems (through Λ) from a thermodynamic measurement.
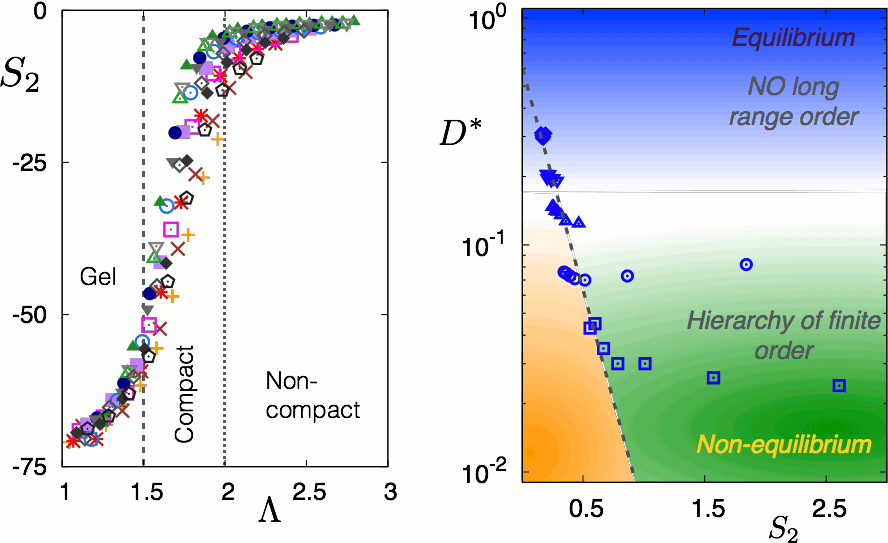
(right panel) Universal relation between average dynamics and structural randomness of systems with competing interactions. Different type of points represent different bulk temperature of the systems, starting from top: T=0.25, 0.20, 0.15, 0.10, 0.05. At high temperature, all the systems behave like equilibrium liquid irrespective of the details of competition and have same diffusivity and same randomness (S2). With decreasing temperature, geometric frustration resulting from competition start to win over thermal fluctuations and non-ergodic aggregates of different shapes start to appear. Reduced diffusivity, D* and S2 quantifying randomness show spread accordingly. Interestingly, same relationship holds for high temperature equilibrium liquid and low-temperatuer non-equilibrium non-compact aggregates. Compact aggregates deviate from that.
Geometric frustration inherent to the competing interactions plays the key role in determining the dynamics of such aggregate forming systems. This very fact has been unattended so far as contemporary studies have relied heavily on the preparation protocol. Usually, the aggregates are prepared by abruptly quenching a high temperature equilibrium liquid to a very low temperature. While this process is good for all practical purposes, it poses serious difficulty for the fundamental understanding of dynamics by pushing it immediately out of equilibrium. By choosing a very slow cooling protocol, we have minimised the protocol dependence and studied both average and microscopic dynamics of the system. Further, we mention that studying the aggregation process is not our focus, rather we concentrate on the post-aggregation steady state dynamics of the system. From the evolution of energy fluctuations in this steady state, it is evident that the system remains non-ergodic over a considerable observation time even in absence of any external perturbation. Such non-ergodic behaviour is observed only when bulk temperature of the system becomes lower than certain value. This value is surprisingly close to the liquid-gas phase separation critical temperature for a system with only attractive interaction and no repulsion. Systems above this temperature behave like equilibrium liquids showing usual long-time diffusion. Below this critical temperaure, the system is sub-diffusive at long time and developes an intermediate time second relaxation which is indicative of heterogeneous dynamics in the system. Most importantly, the temporal heterogeneity is in accord with the variations in local spatial structures. By careful examination of particle displacement fluctuation, we have identified the difference in the microscopic mechanism of dynamics for finite-size compact and non-compact clusters. While the particles in the former are caged by their nearest neighbours, the particles in the later experience strong bonding with their nearest neighbours. Interestingly, this study reveals a universal relationship between diffusivity and structural randomness of the system. The diffusivity is always exponentially related to the exponential of the configurational space available to the system determined by the two-body excess entropy. As long as the system remains sufficiently random (equilibrium liquid or non-ergodic non-compact aggregates) this relation holds. With the appearance of compact crystalline structures, this relation breaks down.
In summary, this study establishes phenomenological relationship among the structural randomess, thermodynamic observables and average dynamics for a generic non-equilibrium pattern-forming system with competing interactions.
3.1 Drop impact on a soap film
Impinging drop on inclined flowing soap films can lead to three possible regimes of post-impact dynamics: (a) the drop bouncing off the film plane, (b) the drop coalescing with the downstream flow, and (c) the drop piercing the film and tunneling through it. The interaction between the film and the drop also presents the unique opportunity to explore the hydrodynamic effects and the elastic properties of soap films, influencing a single phenomenon in tandem.
We perform an experimental study of droplet impacts on a soap film flow, for a number of inclination angles of the film and heights of fall of the drop. The film thickness is approximately in the order of 10 μ and the drop diameter is approximately 1 mm. We mostly observe the bouncing-off regime for smaller angles of film inclination (<20°, to the pre-impact free fall direction of the drop). However, for higher angles of impact, puncture of the film (drop tunneling through) becomes a more common occurrence. The experimental studies are supplemented with an analytical model that characterizes the three impact types through a parametric study of the related phase behavior.
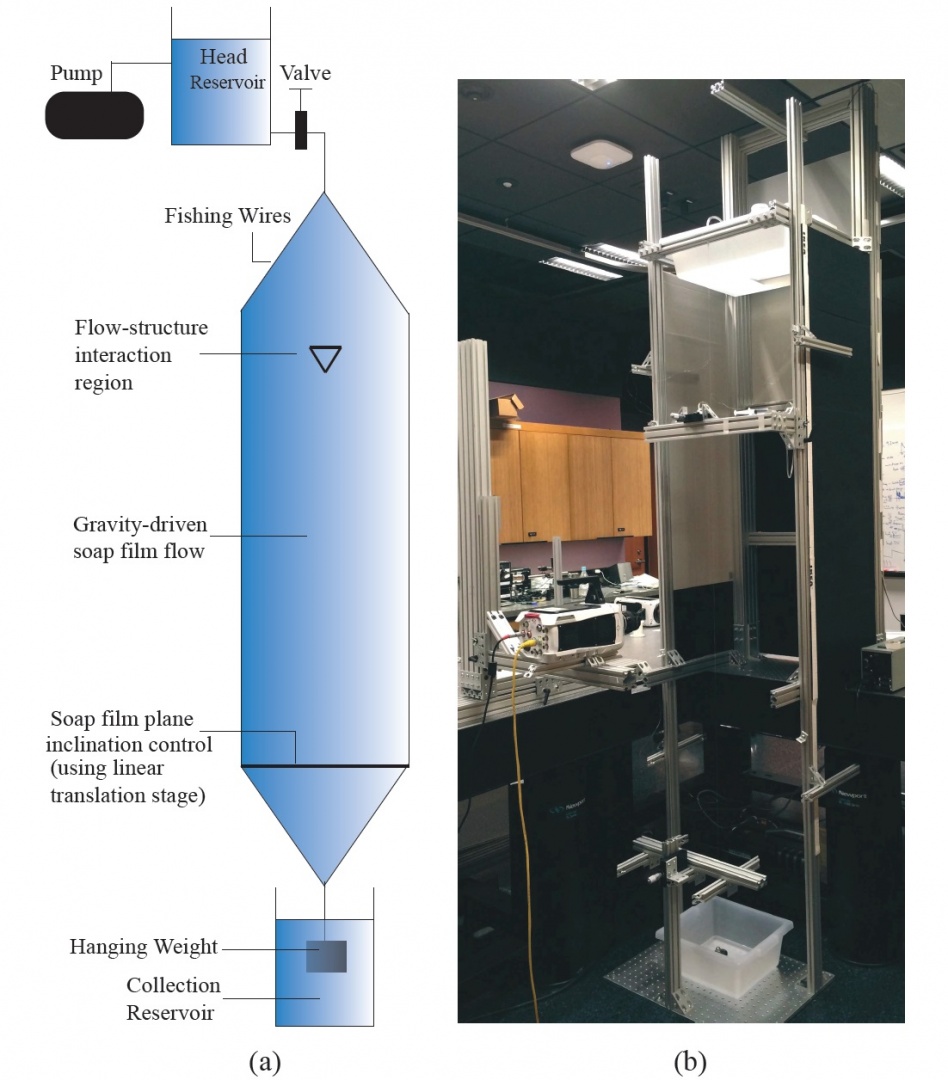
(a) Schematic diagram of the experimental setup. (b) Actual setup
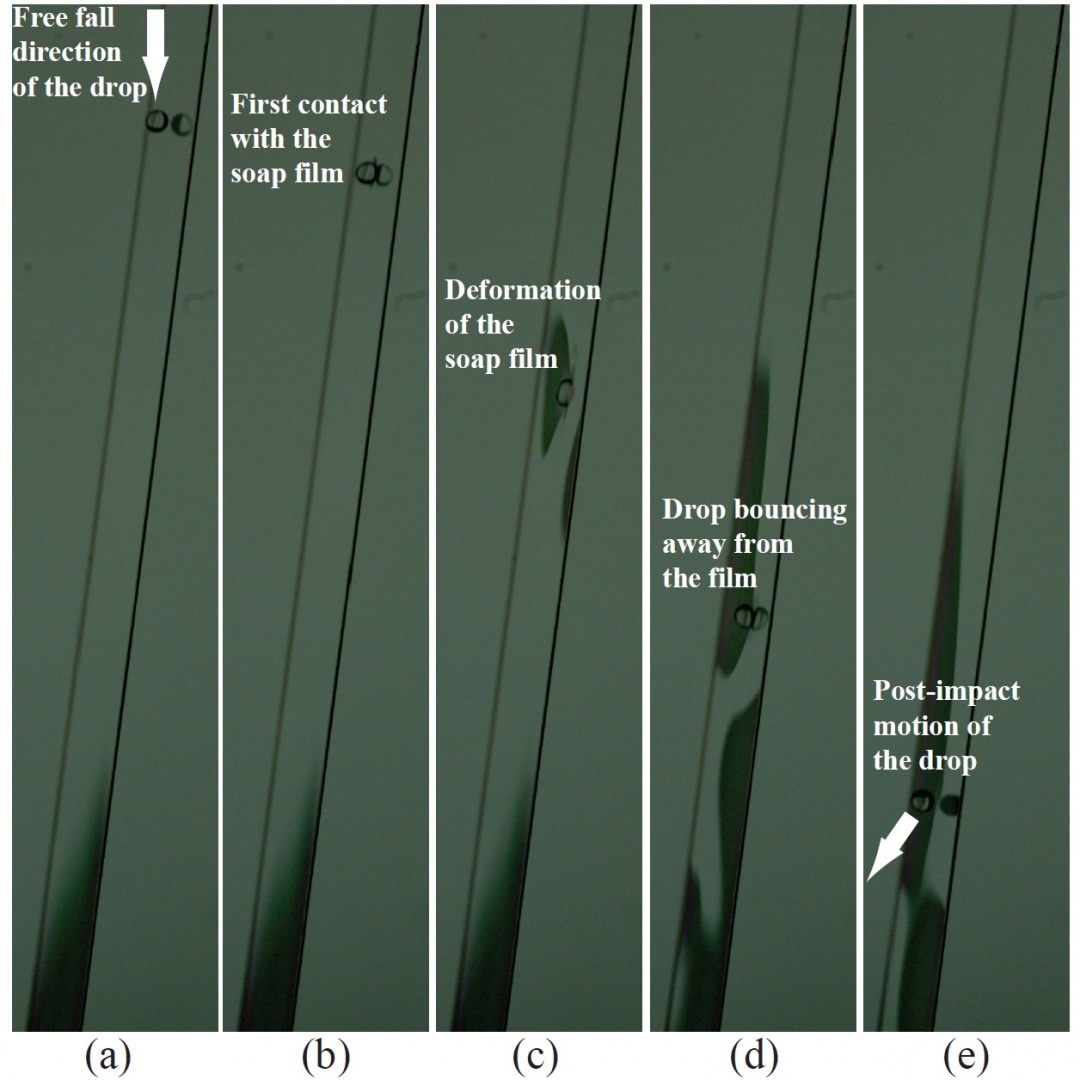
Different stages of the impact. The images are taken from the side (line of sight is almost in plane with the flowing soap film).

Vortex dipole formed on an inclined flowing soap film from impinging drops. This was imaged from the front. A monochromatic sodium lamp was used as the light source to detect the interference fringe patterns.
Model Segment I
- Considers the force non-equilibrium (transverse to the film plane) necessary for bouncing off.
- Forces to be considered: interfacial tension, buoyancy, weight of the drop, elastic deformation forces. It is to be noted that the other hydrodynamic effects are in-plane with the film and hence do not affect the transverse direction dynamics.
- Develops a force-based criterion, as a function of the spread radius of the drop at impact and the angle of inclination of the soap film.
- Plots the force criterion contours on the 2D phase space comprising angle of inclination of the film and spread out radius of the drop during impact.
- Compares the experimental data on the bouncing-off cases with the model.
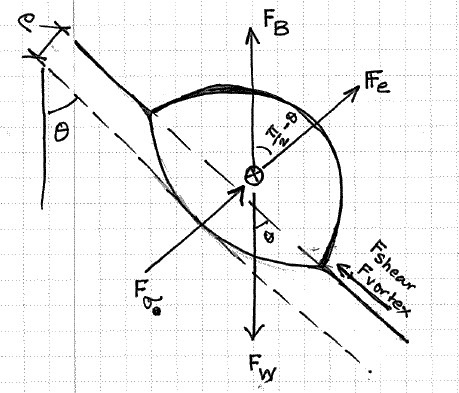
Forces considered during the force balance while considering the bouncing-off criterion
Model Segment II
- Calculates the energy of the drop.
- Theorizes an energy criterion; whereby if the drop energy exceeds the surface energy, then the drop pierces the film apart i.e. tunneling-through ensues.
- Energy criterion will include the hydrodynamic effects and the momentum transfer arguments (from the impacting drop cascading down to the shear layers and the vortex roll-ups).
- Relevant phase space will be on the 2D phase domain of free fall height of the drop (alternatively, the pre-impact velocity of the drop) and spread out radius of the drop during impact.
An additional aspect of the model explores the momentum transfer from the impacting drop to the film flow and identifying the flow features (shed vortices, waves etc.) to which the lost momentum gets diffused out.
4. Publications
4.1 Journals
Nothing to report
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Bandi, M. M. Foot in motion: Mechanics and Control, in 14th HFSP Annual Awardees Meeting, Lugano, Switzerland, 2014.07.09 (2014).
- Das, T. Repulsion dictates non-equilibrium dynamics and structural transitions in two-dimensional aggregates, in Flowing Soft Matter: Bridging the Gap between Statistical Physics and Fluid Mechanics, Udine, Italy, 2014.07.03 (2014).
- Basu, S., & Stremler, M. Mathematical models for exotic wakes, in 67th Annual Meeting of the APS Division of Fluid Dynamics, San Francisco, USA, 2014.11.25 (2014).
- Das, T. Two-dimensional aggregates from competing interactions: Dynamics and Morphology, in International conference on Soft matter ICSM2014, Malavya National Institute of Technology, Jaipur, India, 2014.10.09 (2014).
- Bandi, M. M. Grid scale fluctuations and forecast error in wind power, in Department of Physics & Astronomy, University of Pittsburgh, Pittsburgh, USA, 2014.12.08 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in Indian Institute of Science Education and Research, Mohali, India, 2014.10.03 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in National Chemical Laboratory, Pune, India, 2014.10.13 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in Indian Institute of Science Education and Research, Pune, India, 2014.10.14 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in TIFR Center for Interdisciplinary Sciences, Hyderabad, India, 2014.10.16 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in Jawharlal Nehru Centre for Advanced Scientific Research, Bangalore, India, 2014.10.22 (2014).
- Das, T. Geometric universality of two-dimensional aggregates, in Institute of Physics, Bhubaneswar, India, 2014.10.30 (2014).
- Bandi, M. M. The Spectrum of Wind Power Fluctuations, CMU Electric Energy Industry Center, Carnegie Mellon University, 2015.02.25.
- Das, T. & Bandi, M. M. A single parameter description of aggregate morphologies in two dimensions, in APS March Meeting 2015, San Antonio, Texas, USA, 2015.03.02 (2015).
- Das, T. & Bandi, M. M. Dynamics across the morphological transition in two-dimensional aggregates, in APS March Meeting 2015, San Antonio, Texas, USA, 2015.03.02 (2015).
- Mukherjee, A., & Bandi, M. M. Spatio-temporal dynamics of brittle fracture in particle rafts, in APS March Meeting 2015, San Antonio, Texas, USA, 2015.03.02 (2015).
- Das, T. A curious case of two-dimensional aggregates: in sync spatio-temporal heterogeneities, in Center for Nonlinear Studies, Los Alamos National Laboratory, USA, 2015.03.25 (2015).
5. Intellectual Property Rights and Other Specific Achievements
5.1 Intellectual Property
- US Provisional Patent: System and method for obtaining three components of force based on photoelasticity (2014).
- Inventors:
- Professor Madhusudhan Venkadesan, Yale University, USA
- Professor Shreyas Mandre, Brown University, USA
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Inventors:
- US Provisional Patent: Grid-scale fluctuations and forecast error in wind power (2014).
- Inventors:
- Professor Mahesh M. Bandi, OIST Graduate University, Japan
- Inventors:
5.2 External Grants
- Grant Title: Foot in Motion: Materials, Mechanics & Control
- Funding Agency: Human Frontier Science Program, Strasbourg, France
- Funding: USD 350,000 per year (Sept 2013 - Aug 2016)
- Collaborators:
- Professor Madhusudhan Venkadesan, National Centre for Biological Sciences, India (PI)
- Professor Shreyas Mandre, Brown University, USA (Co-PI)
- Professor Mahesh M. Bandi, OIST Graduate University, Japan (Co-PI)
6. Meetings and Events
6.1 Seminars
1. Title: Mechanics and Geometry of Complex Structures: A pathway towards functions of forms
- Date: June 17, 2014
- Venue: OIST Campus Lab1
- Speaker: Mr. Marcelo Azevedo Dias (Brown University, USA)
2. Title: Complex Energy Systems
- Date: November 4, 2014
- Venue: OIST Campus Center Building
- Speaker: Dr. Michael Chertkov (Los Alamos National Laboratory, USA)
3. Title: From Vortex Reconnections to the Micro Big-Bang in Quantum Fluids
- Date: November 12, 2014
- Venue: OIST Campus Center Building
- Speaker: Professor Itamar Procaccia (The Weizmann Institute of Science, Israel)
4. Title: Earthquakes in the Laboratory: Continuum-granular coupling
- Date: November 18, 2014
- Venue: OIST Campus Center Building
- Speaker: Dr. Scott Backhaus (Los Alamos National Laboratory, USA)
5. Title: Information-driven approach to materials discovery and design
- Date: November 20, 2014
- Venue: OIST Campus Center Building
- Speaker: Dr. Turab Lookman (Los Alamos National Laboratory, USA)
6.2 OIST Workshop: Dynamics at Interfaces https://groups.oist.jp/ja/di/invited-speakers
- Date: June 9-13, 2014
- Venue: OIST Campus
- Co-organizers:
- Speakers:
- Professor Rachel Levy, Associate Professor, Harvey Mudd College, USA.
- Professor David Quéré, Professor, ESPCI, France.
- Professor Ho-Young Kim, Associate Professor, Seoul National University, South Korea.
- Professor Shankar Ghosh, Associate Professor (G), Tata Institute for Fundamental Research, India.
- Professor Hepeng Zhang, Assistant Professor, Shanghai Jiao Tong University, China.
- Professor Anne Juel, Associate Professor, Manchester University, United Kingdom.
- Professor Eric Corwin, Assistant Professor, University of Oregon, USA.
- Professor Masao Doi, Professor, Beihang University, China.
- Professor Linda Cummings, Associate Professor, New Jersey Institute of Technology, USA.
- Professor William Irvine, Assistant Professor, University of Chicago, USA.
- Professor Michael Dickey, Associate Professor, North Carolina State University, USA.
- Professor Hans-Jürgen Butt, Professor, Max Planck Institute for Polymers, Germany.
- Professor Kathleen Stebe, Professor, University of Penssylvania, USA.
- Professor Satoshi Nakata, Professor, Hiroshima University, Japan.
- Professor Keng-Hui Lin, Associate Professor, Academia Sinica, Taiwan.
7. Other
Nothing to report.



