FY2021 Annual Report
Mechanics, and Materials Unit
Professor Eliot Fried

Abstract
FY2021 was another productive year for the Mechanics and Materials Unit. During this period, unit members published 8 peer-reviewed journal articles. They also kept busy with an unprecedented number of diverse outreach activities in Okinawa. A Grant-in-Aid for Scientific Research and a Grant-in-Aid for Early Career Scientists were awarded.
1. Staff
As of March 31, 2022
- Dr. Eliot Fried, Professor
- Dr. Johannes Schönke, Staff Scientist
- Dr. Stoffel Janssens, Staff Scientist
- Dr. Vikash Chaurasia, Postdoctoral Scholar
- Dr. Burhannudin Sutisna, Postdoctoral Scholar
- Dr. Nicholas Mario Wardhana, Postdoctoral Scholar
- Dr. Smriti, Postdoctoral Scholar
- Dr. David Vazquez Cortes, Research Unit Technician
- Mr. Michael Grunwald, Research Unit Technician
- Mr. Dmitrii Koldaev, Graduate Student
- Mr. Alexandru Mihai, Graduate Student
- Mr. Ali Rahmani, Graduate Student
- Ms. Akyl Shakir, Graduate Student
- Dr. Vishesh Bhat, Visiting Researcher
- Ms. Naoko Tokumoto, Research Unit Administrator
Alumni
- Dr. James Kwiecinski, JSPS Postdoctoral Fellow
- Dr. Adel Fernando Sarmiento Rodriguez, Postdoctoral Scholar
- Mr. Louie John Gozun, Research Intern
- Mr. Genki Oyafuso, Research Intern
- Mr. Yuki Odo, Research Intern
- Mr. Sutashu Tomonaga, Research Intern
- Mr. Sandeep Rajendra Kumar, Graduate Student
2. Collaborations
2.1 Unstretchable two-dimensional materials
- Type of collaboration: Joint research
- Researchers:
- Professor Yi-Chao Chen, University of Houston, Houston, TX, USA
- Professor Roger Fosdick, University of Minnesota, Minneapolis, MN, USA
- Professor Brian Seguin, Loyola University Chicago, IL, USA
2.2 Fabrication of diamond-based surface-acoustic-wave devices
- Type of collaboration: Joint research
- Researchers:
- Professor Satoshi Fujii, Okinawa National College of Technology, Naha, Okinawa, JAPAN
2.3 Modeling of size-dependent crystal plasticty in TRIP steel
- Type of collaboration: Joint research
- Researchers:
- Professor Takeshi Iwamoto, Academy of Science and Technology, Hiroshima University, JAPAN
2.4 Flows of thin films on curved substrates
- Type of collaboration: Joint research
- Researchers:
- Professor Daisuke Takagi, University of Hawaii at Mānoa
2.5 Fluid flows in gel networks
- Type of collaboration: Joint research
- Researchers:
- Professor Fernando Duda, Federal University of Rio de Janeiro
- Professor Angela Souza, Federal University Fluminense
2.6 Effects of incompatibility in fluid flows
- Type of collaboration: Joint research
- Researchers:
- Professor Roger Fosdick, University of Minnesota
2.7 Microscopic models for the rheological properties of novel suspensions
- Type of collaboration: Joint research
- Researchers:
- Professor A. Jeffrey Giacomin, Queen's University
- Ms. Mona Kanso, Queen's University
2.8 Randersian geometry and thermodynamics
- Type of collaboration: Joint research
- Researchers:
- Professor Manolis Vevakis, Duke University
- Dr. Martin Lesueur, Duke University
- Mr. Alexandre Guével
3. Activities and Findings
3.1 Two-dimensional simulations of nanocrystalline diamond film growth
Two-dimensional simulations are used to explore topological transitions that occur during the formation of nanocrystalline diamond films grown from nanodiamond grains that are seeded on substrates [1]. Simulations are done for a relatively large range of the initial value Φs of the grain surface fraction Φ. The morphology of porous films is captured at the transition when grains connect to form a one-component network. This is done using newly developed raster-free algorithms that combine computational geometry and network theory. The morphology of porous films and their suspended counterparts is obtained by studying the pore surface fraction Φp, the pore over grain ratio, the pore area distribution, and the contribution of pores of certain chosen areas to Φp. Pinhole survival is evaluated at the transition when film closure occurs using survival function estimates. The morphology of closed films (Φ = 1) is also characterized and is quantified by measuring grain areas and perimeters. The majority of investigated quantities are found to depend sensitively on Φs and the long-time persistence of pinholes exhibits critical behavior as a function of Φs. In addition to providing guidelines for designing effective processes for manufacturing thin films and suspended porous films with tailored properties, this work may advance the understanding of continuum percolation theory.

Reference: [1] S. D. Janssens et al., Acta Mater. 255, 117555 (2022)
3.2 Coordinate-free compatibility conditions for deformations of material surfaces
Material surfaces are fundamental to all theories of thin-walled plates and shells, whether established asymptotically with reference to three-dimensional theory or formulated directly, and have also been used extensively to model adhesive interphases in composites, surface coatings, and thin films. The kinematical framework needed to describe the deformation of a material surface relies intimately on tools and results from classical differential geometry. Orthodox presentations of this subject typically begin by introducing coordinate charts for the reference and deformed configurations of the material surface and hinge on representing fundamental kinematical objects through their components relative to the coordinates associated with said charts. This work supplies a nonstandard treatment that is resolutely coordinate free and, thus, is completely intrinsic. It also provides a basis for studying deformations of kinematically constrained material surfaces and the formulation of variational problems for determining equilibrium configurations of elastic material surfaces characterized by frame-indifferent stored energy densities that depend on the first and second gradients of the deformation.
3.3 Evolution of nanodiamond seeds during the chemical vapor deposition of diamond on silicon substrates in oxygen-rich plasmas
Nanocrystalline diamond (NCD) films formed by chemical vapor deposition (CVD) maintain many outstanding characteristics of microcrystalline diamond films and coatings without the disadvantage of a high surface roughness and are appealing for diverse applications such as machining, sliding and rotating bearings, field-induced electron emission, dentistry, biomedicine and biotechnology, and sensing via micro- and nanoelectromechanical systems. The quality of NCD material by the CVD method is strongly dependent on both the nucleation process and the growth conditions. A high nucleation density hinders the formation of voids at the substrate-film interface improving film adhesion, reduces undesired non-diamond carbon inclusions and leads to smoother deposits. The growth parameters afford control over the grain size and the crystal orientation and also of the purity of the material and other physical properties. Nucleation is especially challenging because NCD films and coatings are typically deposited on foreign substrates that are physically and chemically dissimilar to diamond. Tight control of the nucleation process, of the grain size and of the inter-grain and intra-grain impurities of NCD films is of paramount importance. Adding a small amount of oxygen to the hydrocarbon and hydrogen gas mixture is one way of improving NCD film quality. Oxygen indeed hinders the formation of non-diamond carbon and the incorporation of foreign atoms such as hydrogen, boron, and silicon. In this work, silicon (001)-oriented substrates were seeded with detonation nanodiamonds density and were exposed to a plasma containing methane, hydrogen, and oxygen. The methane concentration and the plasma power were chosen low and high, respectively, to achieve superior film quality. The stability of the nanodiamonds in the oxygen-rich plasma was studied as a function of the chamber pressure and the sample temperature by means of in situ laser interferometry and ex situ secondary electron microscopy (SEM). For deposition conditions that permitted film growth, NCD films were characterized using ex situ SEM, white light reflectometry, atomic force microscopy (AFM), Raman spectroscopy and x-ray diffraction (XRD). It was found that the chamber pressure plays a more crucial role than the substrate temperature in promoting film growth. Furthermore, plasma settings that revealed unsuitable to initiate seed growth on a chemically dissimilar surface such as silicon could be successfully employed to grow NCD films on a 55 nm thick NCD precursor layer deposited without an oxygen admixture.

3.4 The dynamics of incompressible fluids with incompatible distortion rate
This effort is aimed at exploring the implication of allowing the gradient of the velocity field in a flowing fluid to be the sum of two smooth components, both of which are incompatible in the sense that they are not gradients of vector fields. Wile one of these components embodies a smooth distribution of slippage, the other describes the repair needed to ensure that the distortion rate is the gradient of the velocity field. These considerations lead to a generalization of the Navier–Stokes equations for an incompressible fluid. A tensor field characterizes incompatibility is introduced and a fundamental equation for its evolution is proposed. Properties of these equations are exemplified by revisiting the classical problem of pressure-driven flow in a plane, rectangular channel. For a sufficiently large instantaneously applied pressure drop, a novel action due to the diffusivity associated with the transport of incompatibility is illustrated in addition to the normal diffusive and dissipative affect of viscosity. The steady state of the velocity and incompatibility is governed by a system of two ordinary differential equations which are fully analyzed and the resulting fields are determined and discussed. The transient problem is solved numerically and the graphical results show how these fields are structured in time by diffusion and dissipation in the channel during the transition from rest to steady state. A precursor laminar flow persists until a particular time at which the wall shear stress becomes equal to an a priori given cut-off value that initiates incompatibility at the walls of the channel. This incompatibility diffuses inward and interacts synergistically with the viscous action present in the channel to flatten the velocity profile so as to take on a `plug flow-like' appearance, and to redistribute the viscous dissipation and the dissipation due to incompatibility into boundary layers at the channel walls. Certain features of the solutions of these problems consideredresemble results from established theories for laminar flows of non-Newtonian fluids and turbulent flows of incompressible Newtonian fluids. These similarities are suggestive of connections that we find intriguing and plan to pursue in future works.
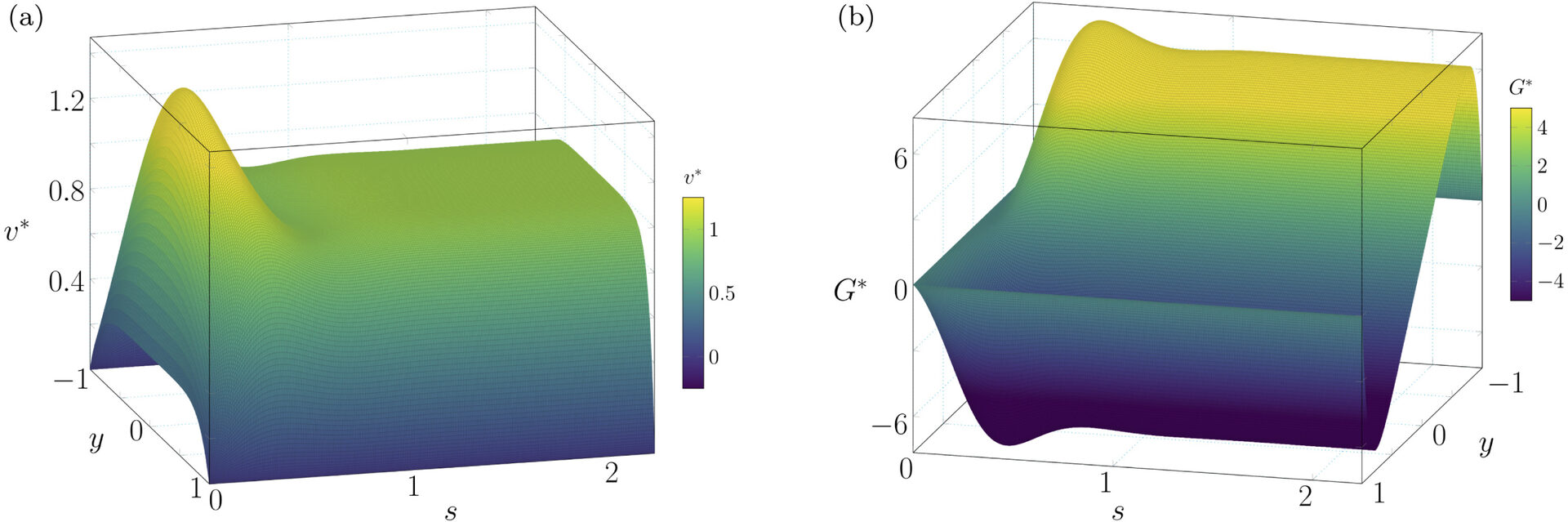
3.5 Fluid flow and interface motion in gels: A finite-strain theory and its application to a channel flow problem
A polymer gel is a two-component material composed of a cross-linked polymer network and a liquid that fills the interstitial space of the network. These materials display unusual and complex behavior due to the coupling between large network distortions and liquid permeation. This interplay gives rise to volumetric phase transitions among other interesting and complex phenomena. We develop a theory for coupled deformation and liquid permeation in polymer gels, allowing for large strains and rotations in conjunction with sharp interfaces separating regions of high and low polymer volume fraction. The theory is applied to pressure-driven liquid flow through a gel-filled rectangular channel, with the aim of investigating how the elastic and osmotic properties of the gel influence the resulting permeation process. Apart from streamwise flow in the direction of the applied pressure drop, the permeation process may involve transverse flow if the elastic response of the gel allows the normal stress acting on a plane parallel to the channel walls to be affected by the shear stress acting on the same plane. For certain elastic energy densities, including those of neo-Hookean and Mooney type, liquid permeation takes place exclusively in the direction of the applied pressure drop. Otherwise, spanwise permeation driven by the contribution to the normal stress distributed on planes parallel to the channel walls is also present. In contrast to the downstream flow, the transverse flow is transient and is accompanied by changes in composition leading to a nonuniform polymer distribution across the channel and thereby influencing the downstream flow profile. By analyzing the short-time response of the gel, we determine the driving force for the transverse flow and show that for strain-stiffening networks the transverse motion of the interstitial liquid is directed inward from the channel walls and that the polymer network motion spreads outward from the center of the channel toward the walls. The opposite occurs for strain-slackening networks. By analyzing the steady-state response, we demonstrate that the applied pressure gradient leads to nonuniform transverse distributions of polymer chains than can be continuous or discontinuous. Discontinuous distributions occur for an effective osmotic response involving attractive interactions and are accompanied by the formation of regions of high and low polymer volume fraction separated by sharp interfaces. Finally, we provide illustrative examples for a gel whose elastic and osmotic responses are modeled by the Gent elastic energy density and the Flory–Huggins mixing energy density, respectively.

3.6 Coupled diffusion and phase transition: Phase fields, constraints, and the Cahn–Hilliard equation
This effort focuses on continuum theories for constituent migration in bodies with microstructure described by a scalar phase field. We formulate two continuum theories, one constrained and the other unconstrained, for constituent migration in bodies with microstructure described by a scalar phase field. The theories are built on the same basic principles. In the constrained theory, the concentration and phase field must coincide, whereas in the unconstrained theory those fields are tame to be independent. From these alternative approaches, we provide a new derivation of the Cahn–Hilliard equation. On the basis of that derivation, we find that the Cahn–Hilliard equation can be interpreted as the limiting variant of a system of Allen–Cahn type diffusion equations that arises from the unconstrained theory. We then use numerical simulations of a recently proposed benchmark problem to support this new interpretation. In particular, we find through an error comparison based on varying the dimensionless coupling energy coefficient that the numerical results of the Allen–Cahn type diffusion system converge linearly to those of the Cahn–Hilliard equation as the coupling coefficient tends to zero.
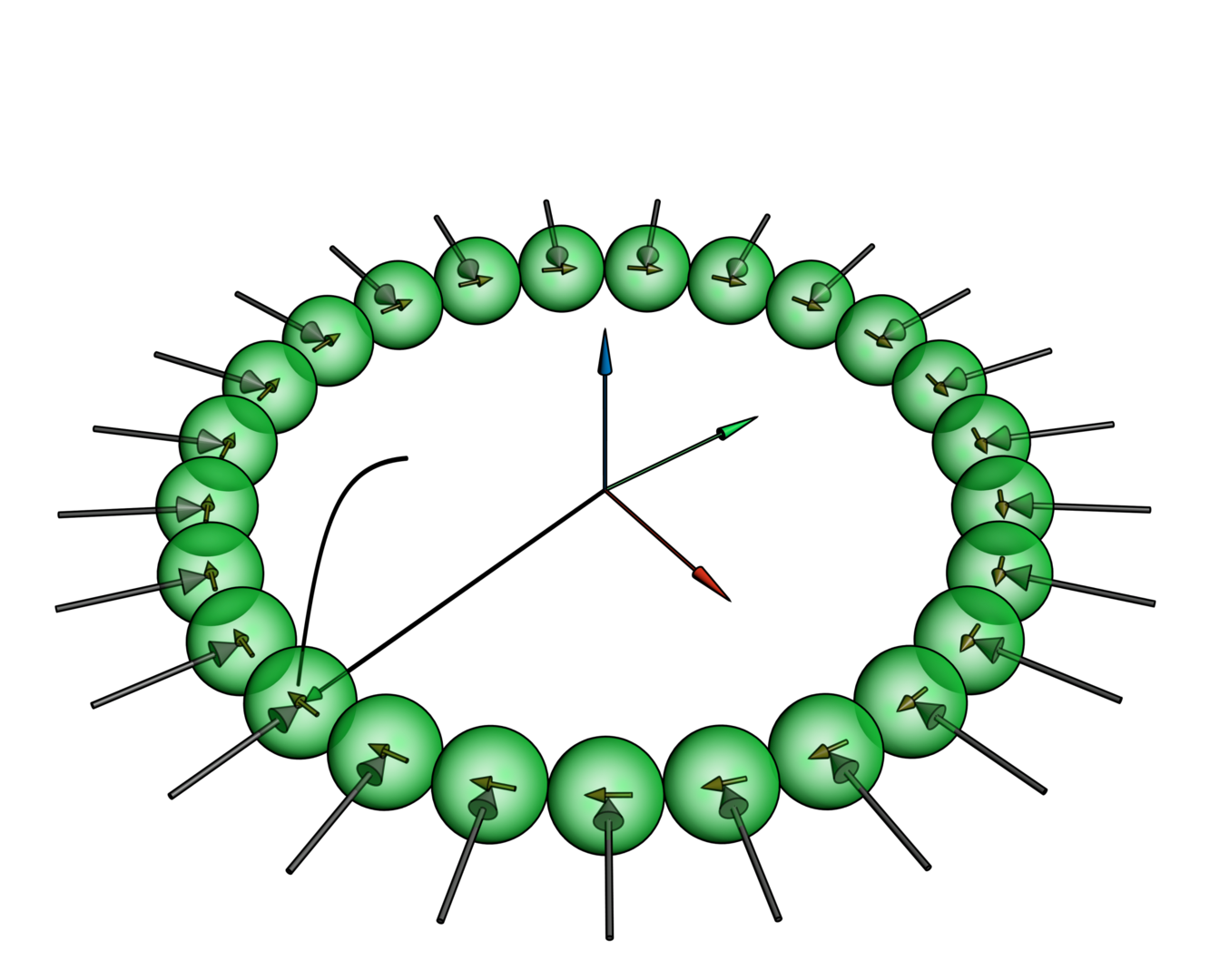
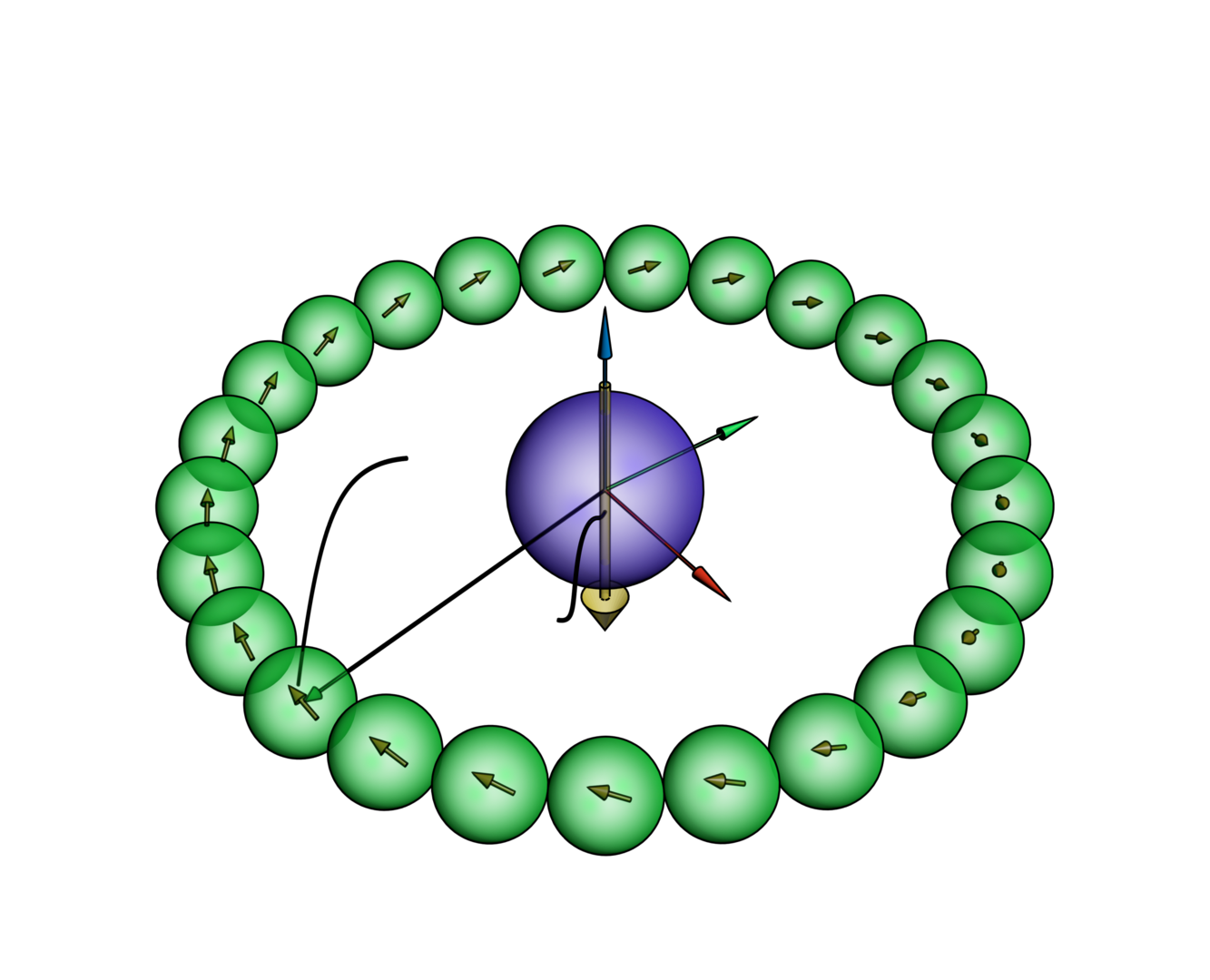
3.7 Summary of the work of T.M. Hoang & D. Vazquez-Cortes onStability of magnetic rings
The assembly of magnetic particles into magnetic rings and their stability play a vital role in many physical systems, i.e. designing switches for non-volatile random-access memory in magnetoelectronic applications, explaining the aggregation processes in colloids, and understanding the origin of the Saturn’s rings. All previous works showed that magnetic rings under the application of an externally homogeneous magnetic field will rupture or break up when instability occurs. We showed for the first time that by using i) an externally heterogeneous magnetic field caused by a magnetic dipole placed at the center of the ring and oriented perpendicular to the plane of the ring or ii) a compressive mechanical load applied at the ring, as illustrated in Figure 1, the magnetic ring can deform without rupture or break
up when instability arises. We also installed an experiment for the first scenario and showed that the observed shape of the ring after instability occurs, as illustrated in Figure 2, agrees well with theoretical calculations. The deformed shapes of our magnetic rings without rupture or break up, owing to high rate of shape changing, could be used to develop novel design concepts for actuators in MEMS or NEMS devices.

|
|
3.8 A continuum theory for mineral solid solutions undergoing chemo-mechanical processes
We derive a thermodynamically consistent framework to characterize the evolution of chemically active minerals. We model the metamorphic mineral assemblages as a solid-species solution where the species mass transport and chemical reaction drive the stress generation process. The theoretical foundations of the framework rely on modern continuum mechanics, thermodynamics far from equilibrium, and the phase-field model. We treat the mineral solid solution as a continuum body, and following the Larché and Cahn network model, we define displacement and strain fields. Consequently, we obtain a set of coupled chemo-mechanical equations. Furthermore, we emphasize the use of the phase-field framework as a promising tool to model complex multi-physics processes in geoscience.
4. Publications
4.1 Journals
- B. Seguin, E. Fried. Coordinate-free compatibility conditions for deformations of material surfaces, Mechanics of Materials 166 (2022), 104193-1–10. (doi:10.1016/j.mechmat.2021.104193)
- A. Giussani, S.D. Janssens, D. Vásquez-Cortés, E. Fried. Evolution of nanodiamond seeds during the chemical vapor deposition of diamond on silicon substrates in oxygen-rich plasmas, Applied Surface Science 581 (2022), 152103-1–11. (doi:10.1016/j.apsusc.2021.152103)
- S.D. Janssens, D. Vásquez-Cortés, E. Fried. Formation and morphology of closed and porous films grown from grains seeded on substrates: two-dimensional simulations, Acta Materialia 225 (2022), 117555-1–11. (doi:10.1016/j.actamat.2021.117555)
- S.P. Clavijo, L. Espath, A. Sarmiento, V.M. Calo, A continuum theory for mineral solid solutions undergoing chemo-mechanical processes, Continuum Mechanics and Thermodynamics. (doi:10.1007/s00161-021-01041-z)
- R. Fosdick, E. Fried. The dynamics of incompressible fluids with incompatible distortion rates, International Journal of Engineering Science 168 (2021) 103540-1–32. (doi:10.1016/j.ijengsci.2021.103540)
- F.P. Duda, A.C. Souza, E. Fried. Fluid flow and interface motion in gels: A finite-strain theory and its application to a channel flow problem, Journal of the Mechanics and Physics of Solids 155 (2021), 104566-1–42. (doi:10.1016/j.jmps.2021.104566)
- T.M. Hoang, D. Vázquez-Cortés. Stability of magnetic rings, International Journal of Solids and Structures 225 (2021), 111060-1–15. (doi:10.1016/j.ijsolstr.2021.111060)
- F.P. Duda, A. Sarmiento, E. Fried. Coupled diffusion and phase transition: Phase fields, constraints, and the Cahn–Hilliard equation, Meccanica 56 (2021), 1707–1725. (doi:10.1007/s11012-021-01338-y)
4.2 Books and other one-time publications
Nothing to report
4.3 Presentations
4.3.1 Oral Presentations
- J. Schönke, A family of periodic functions summing up to a constant when homogeneously distributed, Event: Mathematics of quasiperiodic order and related topics 準周期的秩序の数理とその周辺 (RIMS 共同研究 (グループ型 A)), RIMS + Online via Zoom, Kyoto University, Japan, November 8 (2021).
- B. Sutisna, S.D. Janssens, A. Giussani, D. Vázquez-Cortés, E. Fried, Self-assembled nanocomposites based on block copolymers and nanodiamonds, Oral Presentation (Online) at the 48th World Polymer Congress (IUPAC-MACRO2020+), Jeju, Korea, May 2021
4.3.2 Other Presentations
- S.D. Janssens, B. Sutisna, A. Giussani, D. Vázquez-Cortés, E. Fried, The effect of boundary curvature on the wrinkling of suspended nanocrystalline diamond films, Poster/Exhibition Presentation, Event: 14th International Conference on New Diamond and Nano Carbons (NDNC) 2020/2021, Virtual Conference, June 7-9 (2021)
- B. Sutisna, S.D. Janssens, E. Fried, Guiding Nanodiamond Arrays Using Coassembly with Block Copolymers, Poster Presentation, Event: 14th International Conference on New Diamond and Nano Carbons (NDNC) 2020/2021, Virtual Conference, June 7-9 (2021)
5. Intellectual Property Rights and Other Specific Achievements
5.1 KAKENHI: Grant-in-Aid for Scientific Research
Postdoctoral Fellow: Dr. Stoffel Janssens
Period: From April 2021
5.2 Steering Committee for NDNC2022
Dr. Stoffel Janssens has been elected for the member of steering committee for NDNC2022
NDNC2022
5.3 KAKENHI: Grant-in-Aid for Early Career Scientists
Postdoctoral Fellow: Dr. Burhannudin Sutisna
Period: From April 2020
6. Meetings and Events
6.1 Meetings
6.1.1 Seminars
Professor Meheboob Alam
Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR)
- Date: April 14, 2021
- Venue: Virtual seminar on Zoom
- Seminar: Dynamics and Patterns in Sheared Granular Fluid
6.1.2 Long Term Visiting Researcher
- Professor Yi-chao Chen, University of Houston
6.2 Events
Nothing to report
7. Other
7.1 OIST Press Release: Growing the perfect diamond
Dr. Stoffel Janssens has simulated the growth of both porous and closed polycrystalline diamond films.
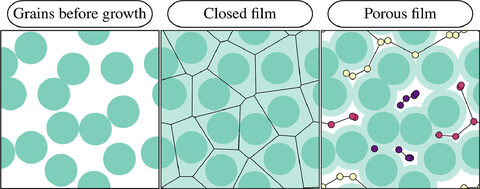
See more at "Growing the perfect diamond: Simulations reveal interesting geometric patterns,"
which was released on Tuesday, 15, February 2022
7.2 Opening ceremony: Kaleidocycle Sculpture "Floating Ring" at Lab4 entrance
On 31 March 2021 the installation of the first Möbius Kaleidocycle sculpture, a self-moving meter-scale object, was finished in the main entrance hall of Lab 4. In a more than two year effort, the sculpture was conceived and designed in the unit and realized in close collaboration with Archimedes Exhibitions Berlin.
Opening ceremony was held on April 1, 2021
https://groups.oist.jp/mmmu/event/floating-ring-kinetic-sculpture-inauguration
Installation of the Möbius Kaleidocycle sculpture in March 2021.



