FY2020 Annual Report

Qubits and Spacetime Unit
Assistant Professor Philipp Höhn

Abstract

Our new group was freshly assembled in the past year with the unit leader joining virtually in the summer of 2020, the first three postdocs joining in October and November 2020 and rotation students in January 2021. On account of the pandemic, the unit leader only arrived physically at OIST in February 2021, while the postdocs had to remain virtual members for FY20. Nevertheless, our group researched on various topics, including quantum clocks and the problem of time, quantum frame covariance in quantum foundations and gauge theories, finite region gauge theories and boundary action principles, and the black hole information paradox. We have also spent efforts pondering about the interplay of quantum correlations and spacetime geometry.

1. Staff

Dr. Joshua Kirklin, Postdoctoral Scholar
Dr. Isha Kotecha, Postdoctoral Scholar
Dr. Fabio Maria Mele, Postdoctoral Scholar
Jiahui Bao, Rotation Student (January - April 2021)
Miguel Jorquera Riera, Rotation student (January - April 2021)
Victor Castillo-Martinez, Collaborator, external (March 2021 - )
Midori Tanahara, Administrative Assistant

2. Collaborations

2.1 Quantum Relational Dynamics

Description: this collaboration resulted in a preprint in July 2020 (which is now published).
Type of collaboration: Joint research
Researchers:
- Prof. Alex Smith, Dartmouth College and Anselm College, USA
- Dr. Max Lock, Institute for Quantum Optics and Quantum Information, Vienna, Austria

2.2 Quantum reference frame transformations as symmetries

Description: this collaboration resulted in a preprint in November 2020.
Type of collaboration: Joint research
Researchers:
- Dr. Markus Müller, Institute for Quantum Optics and Quantum Information
- Marius Krumm, Institute for Quantum Optics and Quantum Information

2.3 Quantum corrected polymer black hole thermodynamics

Description: this collaboration resulted in a preprint in February 2021.
Type of collaboration: Joint research
Researchers:
- Dr. Johannes Münch, CPT Marseille, France
- Stratos Pateloudis, Universität Regensburg, Germany

2.4 Quantum Relativity of Subsystems

Description: this collaboration resulted in a preprint in March 2021.
Type of collaboration: Joint research
Researchers:
- Dr. Max Lock, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Shadi Ali Ahmad, Dartmouth College, USA
- Prof. Alex Smith, Dartmouth College and Anselm College, USA
- Dr. Thomas Galley, Perimeter Institute for Theoretical Physics, Waterloo, Canada

2.5 Edge modes as reference frames and boundary actions from post-selection

Description: ongoing.
Type of collaboration: Joint research
Researchers:
- Dr. Sylvain Carrozza, University of Nijmegen, The Netherlands

2.6 Relational Dynamics with periodic clocks

Description: ongoing.
Type of collaboration: Joint research
Researchers:
- Dr. Max Lock, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Dr. Leonardo Chataignier, University of Köln, Germany

2.7 Quantum frame covariance for general groups

Description: ongoing.
Type of collaboration: Joint research
Researchers:
- Anne-Catherine de la Hamette, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Dr. Thomas Galley, Perimeter Institute for Theoretical Physics, Waterloo, Canada
- Dr. Leon Loveridge, University of South-Eastern Norway
- Dr. Markus Müller, Institute for Quantum Optics and Quantum Information, Vienna, Austria

2.8 Quantum frame covariance and time evolution

Description: ongoing.
Type of collaboration: Joint research
Researchers:
- Dr. Markus Müller, Institute for Quantum Optics and Quantum Information, Vienna, Austria
- Marius Krumm, Institute for Quantum Optics and Quantum Information, Vienna, Austria

3. Activities and Findings

We will only describe the findings of published projects.

3.1 Equivalence of approaches to relational quantum dynamics in relativistic settings

In collaboration with Prof. Alex Smith from Anselm College and Dartmouth College and Dr. Max Lock, we have demonstrated the equivalence of three a priori distinct approaches to relational quantum dynamics in relativistic settings such as appearing in relativistic particle models or quantum cosmology. Relational dynamics becomes a necessity in systems facing the so-called problem of time, arising on account of a temporal diffeomorphism invariance underlying relativity. The idea of relational dynamics is to use dynamical degrees of freedom to serve as a clock relative to which to describe quantum dynamics rather than some idealized and nondynamical background time. Various approaches have been pursued on this question in the quantum gravity and quantum foundations communities. Based on previous works by us, we were able to prove full equivalce of three approaches to the problem, known as (i) relational observables, (ii) the Page-Wootters formalism, and (iii) quantum deparametrizations. Using this equivalence we were also able to resolve a criticism that was levied against the Page-Wootters formalism 30 years ago, demonstrating its consistenty. We were also able to extend a method for describing quantum clock covariance to relativistic settings, allowing us to change from the evolution relative to one quantum clock to the one relative to another. This is a challenging task when the different clocks undergo quantum fluctuations. Using this formalism, we were also able to study the quantum synchronization of quantum clocks, showing that this undergoes a quantum relativity, i.e. synchronization becomes dependent on the quantum clock perspective.

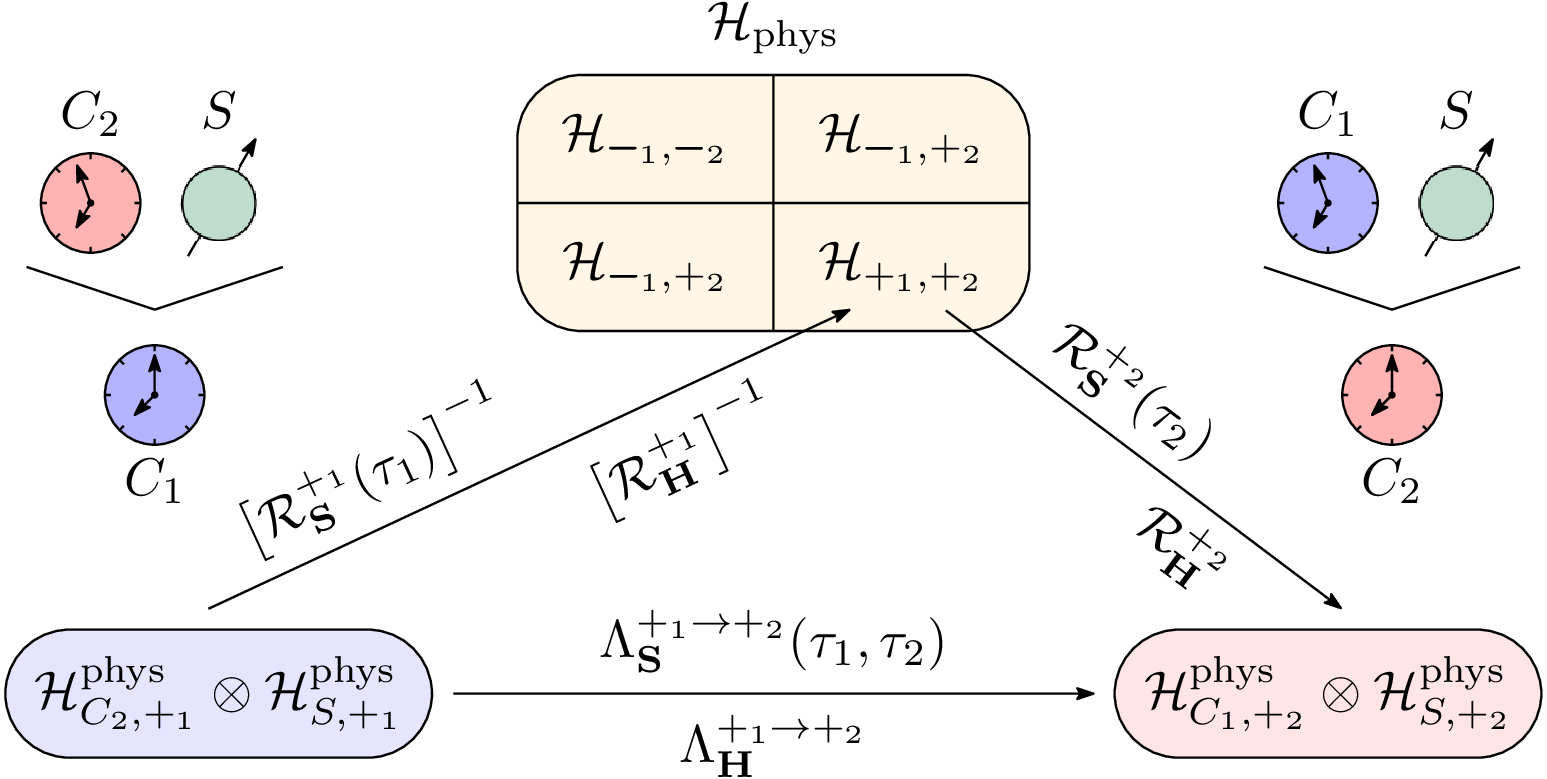
Schematic representation of the "quantum coordinate transformation" representing a quantum clock change.

Publication: Höhn, P., Smith, A., Lock, M., Equivalence of approaches to relational quantum dynamics in relativistic settings, Front. Phys. 9:587083 (2021), invited contribution to special issue "Qubits and Spacetime"

3.2 Quantum reference frame transformations as symmetries and the paradox of the third particle

In a quantum world, reference frames are ultimately quantum systems too -- but what does it mean to "jump into the perspective of a quantum particle"? In work with two collaborators from Vienna, we show that quantum reference frame (QRF) transformations appear naturally as symmetries of simple physical systems. This allows us to rederive and generalize known QRF transformations within an alternative, operationally transparent framework, and to shed new light on their structure and interpretation. We give an explicit description of the observables that are measurable by agents constrained by such quantum symmetries, and apply our results to a puzzle known as the `paradox of the third particle'. We argue that it can be reduced to the question of how to relationally embed fewer into more particles, and give a thorough physical and algebraic analysis of this question. This leads us to a generalization of the partial trace (`relational trace') which arguably resolves the paradox, and it uncovers important structures of constraint quantization within a simple quantum information setting, such as relational observables which are key in this resolution. While we restrict our attention to finite Abelian groups for transparency and mathematical rigor, the intuitive physical appeal of our results makes us expect that they remain valid in more general situations.

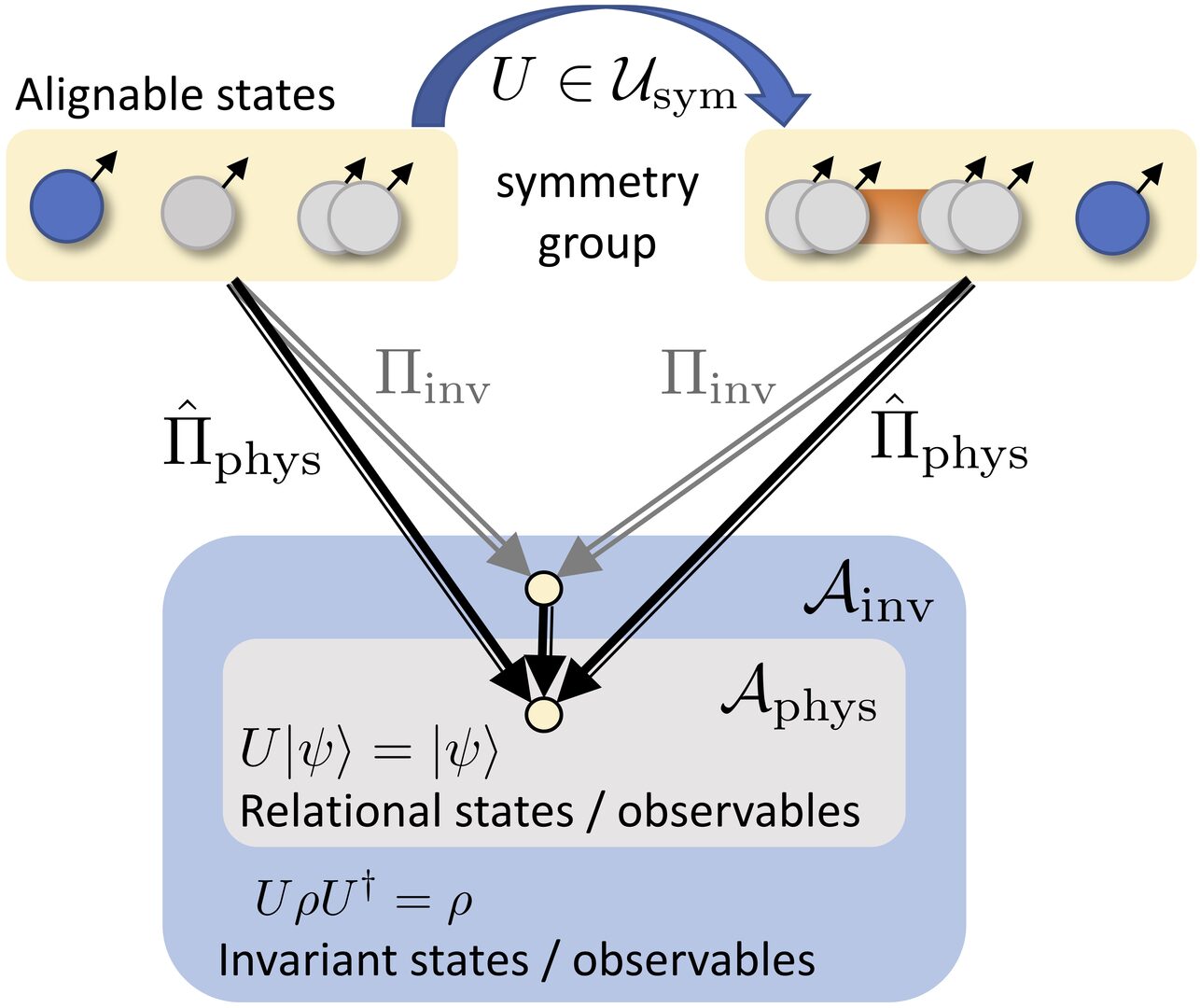
Overview over different kinds of invariant states and observables arising under the symmetry transformations relevant for quantum reference frames.

Publication: Marius Krumm, Philipp A. Höhn, and Markus P. Müller, "Quantum reference frame transformations as symmetries and the paradox of the third particle", arXiv:2011.01951, accepted for publication in Quantum

3.3 Islands and Uhlmann phase: Explicit recovery of classical information from evaporating black holes

Recent work has established a route towards the semiclassical validity of the Page curve, and so provided evidence that information escapes an evaporating black hole. However, a protocol to explicitly recover and make practical use of that information in the classical limit has not yet been given. Our postdoc Josh Kiklin described such a protocol in a single-authored paper, showing that an observer may reconstruct the phase space of the black hole interior by measuring the Uhlmann phase of the Hawking radiation. The process of black hole formation and evaporation provides an invertible map between this phase space and the space of initial matter configurations. Thus, all classical information is explicitly recovered.

Publication: Josh Kirklin, "Islands and Uhlmann phase: Explicit recovery of classical information from evaporating black holes", arXiv:2011.07086

3.4 Quantum corrected polymer black hole thermodynamics: Mass relations and logarithmic entropy corrections

Fabio mele continued his analysis of the effective model of quantum Schwarzschild black holes that he developed with collaborators before joining the unit. In the resulting spacetime of this model the central singularity is resolved by a black-to-white hole bounce, quantum effects become relevant at a unique mass independent curvature scale, while they become negligible in the low curvature region near the horizon and classical geometry is approached asymptotically. This is the case independently of the relation between the black and white hole masses, which are thus freely specifiable independent observables. A natural question then arises about the phenomenological implications of the resulting non-singular effective spacetime and whether some specific relation between the masses can be singled out from a phenomenological perspective. In their paper, Fabio and his collaborators focussed on the thermodynamic properties of the effective polymer black hole and analyse the corresponding quantum corrections as functions of black and white hole masses. The study of the relevant thermodynamic quantities such as temperature, specific heat and horizon entropy reveals that the effective spacetime generically admits an extremal minimal-sized configuration of quantum-gravitational nature characterised by vanishing temperature and entropy. For large masses, the classically expected results are recovered at leading order and quantum corrections are negligible, thus providing us with a further consistency check of the model. The explicit form of the corrections depends on the specific relation among the masses. In particular, a first-order logarithmic correction to the entropy is obtained for a quadratic mass relation. The latter corresponds to the case of proper finite length effects which turn out to be compatible with a minimal length generalised uncertainty principle associated with an extremal Planck-sized black hole.

Publication: Fabio Mele, Johannes Münch, and Stratos Pateloudis, "Quantum corrected polymer black hole thermodynamics: Mass relations and logarithmic entropy corrections", arXiv:2102.04788

3.5 Quantum relativity of subsystems

One of the most basic notions in physics is the partitioning of a system into subsystems, and the study of correlations among its parts. In joint work with collaborators from IQOQI Vienna, Dartmouth College and Perimeter Institute, we explored these notions in the context of quantum reference frame (QRF) covariance, in which this partitioning is subject to a symmetry constraint. We demonstrated that different reference frame perspectives induce different sets of subsystem observable algebras, which leads to a gauge-invariant, frame-dependent notion of subsystems and entanglement. We further demonstrated that subalgebras which commute before imposing the symmetry constraint can translate into non-commuting algebras in a given QRF perspective after symmetry imposition. Such a QRF perspective does not inherit the distinction between subsystems in terms of the corresponding tensor factorizability of the kinematical Hilbert space and observable algebra. Since the condition for this to occur is contingent on the choice of QRF, the notion of subsystem locality is frame-dependent.

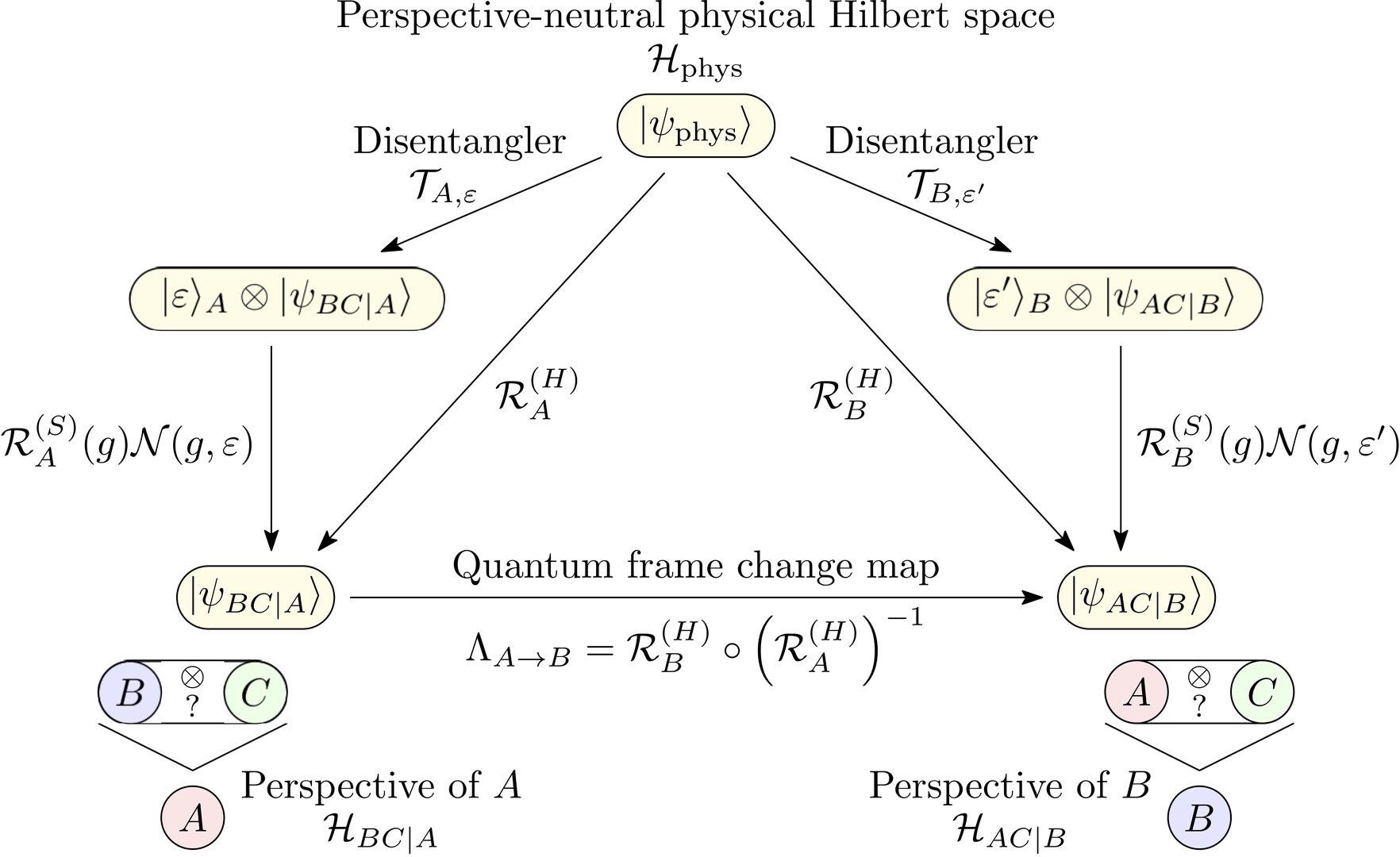
Schematic representation of how quantum frame transformations lead to a relativity of entanglement.

Publication: Philipp A. Höhn, Maximilan P. E. Lock, Shadi Ali Ahmad, Alexander R. H. Smith, and Thomas D. Galley, "Quantum Relativity of Subsystems", arXiv:2103.01232

4. Publications

4.1 Journals

Höhn, P., Lock, M. P. E. Lock, Ahmad, S. A., Smith A. R. H., and Galley, T. D., "Quantum Relativity of Subsystems", arXiv:2103.01232
Mele, F., Münch, J., Pateloudis, S., Quantum corrected polymer black hole thermodynamics: Mass relations and logarithmic entropy corrections, Preprint: arXiv:2102.04788.
Kirklin, J., Islands and Uhlmann phase: Explicit recovery of classical information from evaporating black holes, Preprint: arXiv:2011.07086.
Krumm, M., Höhn, P., Müller, M., Quantum reference frame transformations as symmetries and the paradox of the third particle, Preprint: arXiv:2011.01951, accepted for publication in Quantum.
Höhn, P., Smith, A., Lock, M., Equivalence of approaches to relational quantum dynamics in relativistic settings, Front. Phys. 9:587083 (2021), invited contribution to special issue "Qubits and Spacetime", Preprint: arXiv:2007.00580.
Höhn, P., Vanrietvelde, A., How to switch between relational quantum clocks, New. J. Phys. 22, 123048, doi:10.1088/1367-2630/abd1ac (2020).

4.2 Books and other one-time publications

Nothing to report

4.3 Oral and Poster Presentations

Josh Kirklin, Uhlmann Phase, Black Hole Information and Holography, February 10 2011, Seminar at Albert Einstein Institute in Potsdam-Golm (video)
Philipp Höhn, "Perspective-neutral approach to quantum frame covariance, part II", Nov 30 2020, two-part seminar, Quantum Information Theory Group of ETH Zürich (video).
Philipp Höhn, "Perspective-neutral approach to quantum frame covariance, part I", Nov 17 2020, two-part seminar, Quantum Information Theory Group of ETH Zürich (video).
Philipp Höhn, "Problem of time, relational observables and quantum covariance", Oct 7 2020, inaugural talk of the new international seminar series initiative Quantum Gravity Across Approaches (video).
Höhn, P., Progress in relational quantum dynamics, Sep 15 2020, International LQG Seminar (video).
Josh Kirklin, Uhlmann Phase, Black Hole Information and Holography, March 2nd 2021, Seminar at Institute for Research in Fundamental Sciences (IPM) Tehran.

5. Intellectual Property Rights and Other Specific Achievements