Code - Fujin - Scaling
We test the scaling performance of our solver. In particular, we consider the time evolution of a Taylor-Green vortex in a three-periodic domain of size \(2\pi L\). The velocity field is initialized as
\(u = U \sin \left( x/L \right) \cos \left( y/L \right) \cos \left( z/L \right),\)
\(v = -U \cos \left( x/L \right) \sin \left( y/L \right) \cos \left( z/L \right),\)
\(w=0.\)
The Reynolds number \(Re = \rho U L /\mu\) is fixed equal to \(1600\).

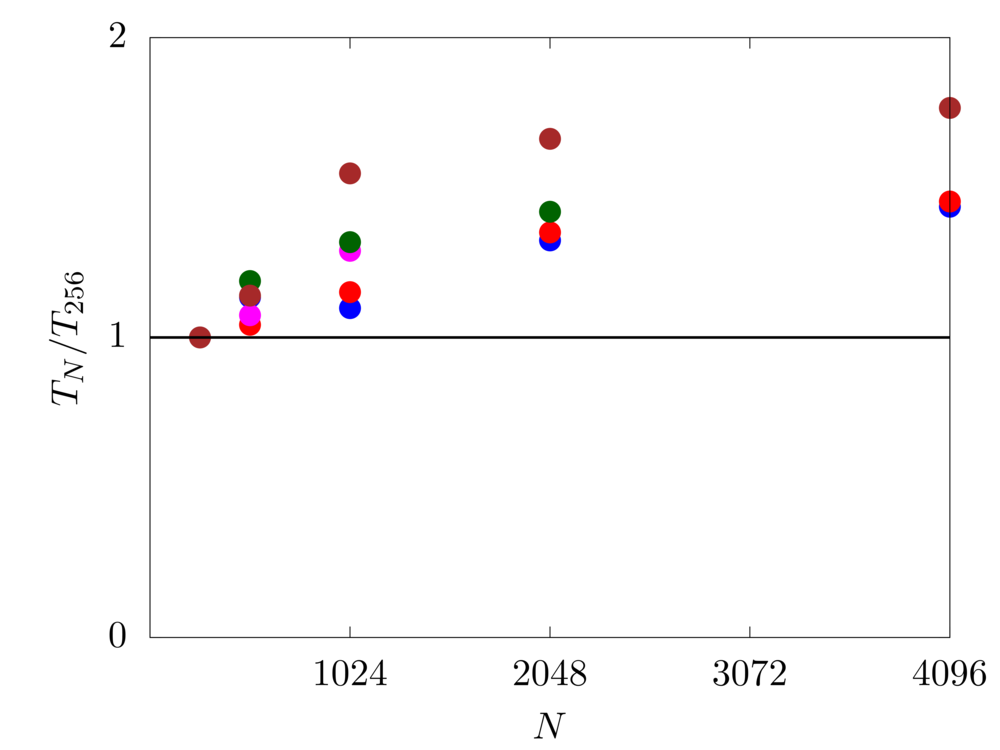
Blue: Beskow - KTH (Sweden)
Red: Oakbridge-CX - UTokyo (Japan)
Magenta: Oakforest-PACS - JCAHPC (Japan)
Brown: SQUID - Handai (Japan)
Green: Deigo - OIST (Japan)
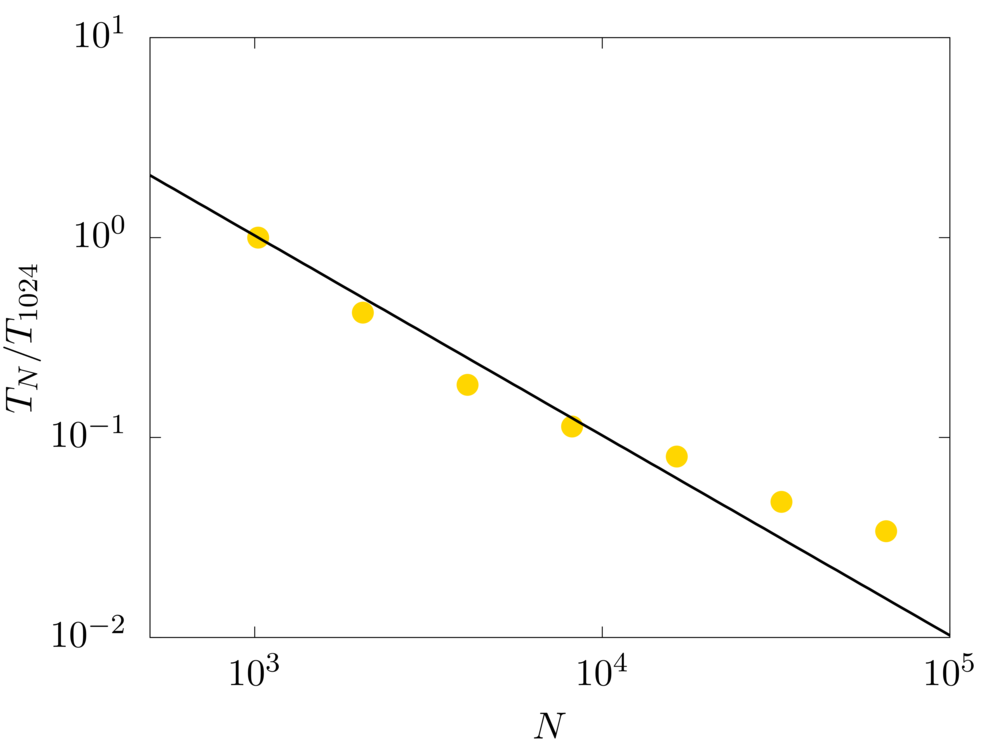
Gold: Fugaku - RIKEN (Japan)
The strong scaling test evaluates the speedup for a fixed problem size with respect to the number of processors. For this test, we consider a numerical domain discretised with \(1024\) grid cell per side. The code shows very good scaling performance up to about \(10^4\)cores, with an almost linear decay of the computational time with the number of cores used.
Blue: Beskow - KTH (Sweden)
Red: Oakbridge-CX - UTokyo (Japan)
Magenta: Oakforest-PACS - JCAHPC (Japan)
Brown: SQUID - Handai (Japan)
Green: Deigo - OIST (Japan)
The weak scaling test evaluates the speedup for a scaled problem size with respect to the number of processors. For this test, we consider a numerical domain discretised with around \(8M\) grid cells per computational sub-domain. The code shows a good scaling with only a small decay of performance from \(N=256\) to \(4096\) cores, suggesting that strong scaling timings can scale up to much larger problem sizes.



