Colloquium: "Simplicial homology, part III" by Dr. Guilherme Sadovski

Speaker: Dr. Sadovski is a member of this unit (visit his page)

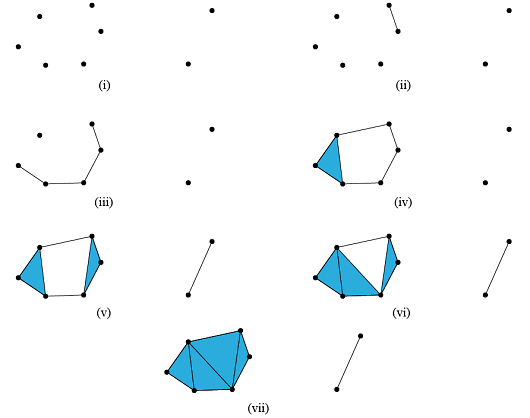
Abstract: Part III of IV in our series will start by the definition of the cycle groups as kernel of the boundary operators. Further, we define the boundary groups as the image of the boundary operator. The homology groups associated with the simplicial complex can then be defined as the groups whose elements are cycles which are NOT boundaries (the "triangles" without interior). From there, we argue that these homology groups are actually topological invariants of the simplicial complex. Further, we show how homology groups are independent of a particular triangulation of X and therefore can be associated to X itself. Finally, we finish by evaluating the homology groups of 0-manifolds and showing that they carry information about the degree of connectedness of such spaces (a topologically invariant information).