[Seminar] "Random coefficients autoregressive processes and the PUCK model with fluctuating potential: application to the diffusion of market prices" - by Mr. Arthur Yamashita

Speaker

Mr. Arthur Yamashita

PhD student at Tokyo Institute of Technology

Abstract

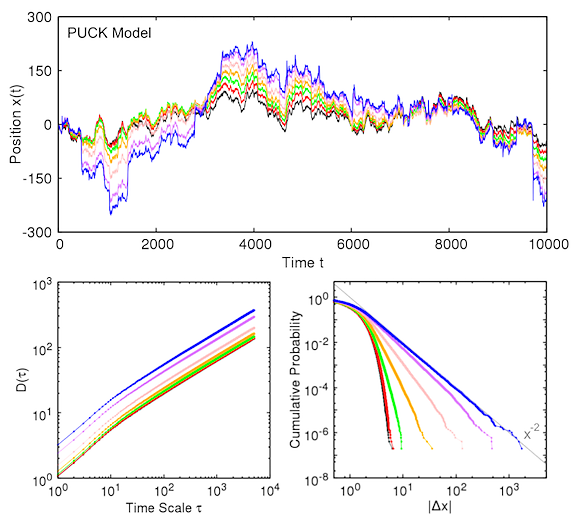
The Potentials of Unbalanced Complex Kinetics (PUCK) model was originally proposed as a representation of the market price dynamics, consisting of a random walker subjected to a potential whose center is located at the moving average of its last positions. In this work we study the PUCK model with fluctuating quadratic potential, created by adding stochastic perturbations to the corresponding deterministic one. We show that the PUCK model with such potential is a special case of the Random Coefficients Autoregressive (RCAR) process and it is naturally connected with the commonly used model for financial time series Autoregressive Conditional Heteroskedasticity (ARCH) process, being both RCAR processes but with different dependence relations among the coefficients. As theoretical results for the general RCAR process considering Gaussian perturbations, we obtain its solution in terms of random generalized Fibonacci numbers and then derive the explicit expression of the mean squared displacement D^2(τ), having the same functional form as the ordinary autoregressive process but amplified by the fluctuations of the coefficients. We also establish the conditions for divergence of the variance, which by the Kesten's theorem imply the tail-index α=2 of the power-law-tailed cumulative probability distribution. Finally, translating those results to the PUCK model, we analyze real data from the U.S. Dollar/Japanese Yen market and demonstrate that the model is successful in reproducing empirical facts of market price time series, namely the diffusion behavior of prices and the heavy-tailed distribution of price changes. As an additional topic, we discuss the mathematical structure responsible for the power-law-tailed distribution in the RCAR process: the sum of products of identically distributed random variables.