FY2012 Annual Report
Mathematical Biology Unit
Associate Professor Robert Sinclair

Abstract
I continue to wonder about how best mathematics and biology can relate to each other. Goethe famously said "Mathematicians are like [foreigners]: if you speak to them, they will translate what you say into their own language, and then it becomes something completely different", and I think there is some truth in this. In mathematical biology, one most work hard to avoid this temptation to translate for as long as possible. A fundamental biological question may easily cease to appear important if translated into equations, and yet the biological importance remains. It is fair to say that I have spent most of my energy this year working on this central issue of communication by communicating with as many specialists as I could find!
1. Staff
- Dr. Robert Sinclair, Associate Professor
- Shino Fibbs, Research Administrator
2. Collaborations
- Theme: Geometry and visualization of integrable systems and non-integrable systems
- Type of collaboration: JSPS Grant 22654010
- Researchers:
- Professor Martin Guest, Waseda University
- Professor Takashi Sakai, Tokyo Metropolitan University
3. Activities and Findings
Almost every morning, I find myself staring at a speaker grille in the lift which takes me up to C floor:

It has left a deep impression on me, one I could not understand myself at first, but now it is finally clear. The appearance of perfection is misleading - one of the holes is "out of place". Does this tell us something? I think it does tell us something. I expect it is telling us that a human being made those holes. Thus, the living world makes itself apparent here through a lack of the type of perfection we mathematicians are used to focus on. It is not difficult to write down mathematical equations which describe a perfect lattice. It is difficult to begin to decribe, in mathematical terms, what it means to say "out of place" and why that may be a sign of life.
The speaker grille also reminds me of one more misleading impression: that "cutting edge science" is somehow shiny and clean. The phrase usually makes me think of people in very white lab coats standing in front of large and shiny metallic machines, usually with vigorously flashing lights. I think this image is misleading because cutting is often a rather messy or dirty process. Indeed, the development of new theory, for research fields which traditionally have had very little, is often a matter of learning from ugly trial and error, rather than a quest for beauty (compare with the work of Paul Dirac, who did in fact very successfully search for beauty in theoretical physics - but that was a field which had already had hundreds of years of mathematical formulation of its theory).
For example, I spent much of this year working with paleontologists (Pat and Tom Rich), in an attempt to formulate a statistical argument which would support or reject a specific hypothesis concerning the classification of a fossil bone. It is not only that fossils are found in dirt or rock, but they are often broken or distorted, so the very idea of using mathematics is often questioned. I have found this work to be enormously rewarding, because one does make progress if one puts in the effort. I think it is fair to say that what has resulted from this rather intense collaboration has been very different from what either I or the paleontologists had first expected to come out, and yet we have put as much of our combined expertise into the final analysis as we could. I will write more about this work when it is eventually published: Truly interdisciplinary work is not easy to get into print.
I am particularly grateful to Makoto Manabe of the National Museum of Nature and Science in Tokyo, who not only allowed me to make measurements of bones in his collection, but also taught me much about the nature of his work.
A highlight from the very beginning of the year was the publication of the work I did with Dr. Yihwa Kim and Prof. Erik de Schutter, on a theoretical argument as to why bifurcations ("forks") in various biological trees, from brain cells to corals, tend to be flat.
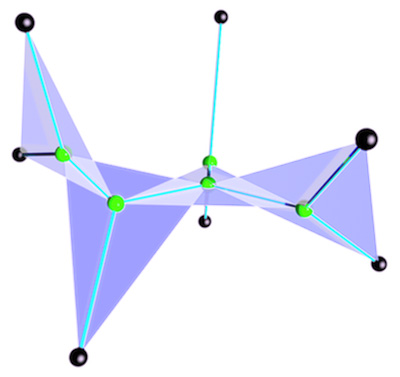
The work was done for tree-like structures (no loops allowed), but this did not seem to be a requirement for the analysis, so I wondered whether bifurcations would also be flat for biological structures which are not tree-like. It seemed that cobwebs would be a good candidate! I traveled to Helsinki to see an exhibition of a digitized Black Widow web which had been scaled up to human size by Tomas Saraceno ( http://www.tomassaraceno.com ):
Some initial analysis of the data provided by Saraceno suggests that cobwebs also have flat bifurcations, but there are significant difficulties separating the actual cobweb from artifacts of the digitization. Work continues on this very nice problem!
While in Helsinki, I also visited the lab of Prof. Dennis Bamford, a virologist with deep theoretical insights which had fascinated me for some time. We have started working on the problem of detecting sequence similarity between highly divergent sequences. I am excited about this work for a number of reasons, and it has become a major activity for me.
Finally, I would like to thank the students of OIST for providing me with much needed energy, by actively participating in classes and allowing me to bend their minds!
4. Publications
4.1 Journals
- Kim, Y., Sinclair, R., Chindapol, N., Kaandorp, J.A., de Shutter, E.; Geometric Theory Predicts Bifurcations in Minimal Writing Cost Trees in Biology Are Flat, PLoS Comput Biol., doi: 10.1371/journal.pcbi.1002474 (2012).
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Sinclair, R. Imperfection at the Cutting Edge, Dynamics of nonlinear oscillations and their applications in neuroscience and biology, Tokyo Metropolitan University, Tokyo, Japan, Apr 13, 2012
- Sinclair, R. Towards a Quantification of Stress in Biological Oscillators, JST/CREST Seminar:Towards Depper Understanding of Biodynamics Principles, Okinawa, Japan, Dec 3, 2012
- Sinclair, R. The Need for Mathematical Neuroscience: Beyond Computation and Simulation, Panel Discussion:, CNS2012, Atlanta/Decatur, GA, USA, June 25, 2012
- Sinclair, R. What are we?, Yamada Jr. High School, Onna-son, Okinawa, Dec 18, 2012
- Sinclair, R. What are we?, OIST Open Campus, Okinawa, March 3, 2013
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Seminar
- Date: July 6th, 2012
- Venue: OIST Campus Lab1
- Speaker: Dr. Anthony Poole (University of Canterbury)
6.2 Seminar
- Date: September 12th, 2012
- Venue: OIST Campus Lab1
- Speaker: Dr. Iain Aitchison (The University of Melbourne)
6.3 Seminar
- Date: January 24th, 2013
- Venue: OIST Campus Lab 1
- Speakers: Dr. Jun Inoue (Atomosphere and Ocean Research Institute, The University of Tokyo)



