生物の非線形力学データサイエンス研究ユニット(ジェラルド・パオ)
The biological nonlinear dynamics data science unit investigates complex systems explicitly taking into account the role of time. We do this by instead of averaging occurrences using their statistics, we treat observations as frames of a movie and if patterns reoccur then we can use their behaviors in the past to predict their future. In most cases the systems that we study are part of complex networks of interactions and cover multiple scales. These include but are not limited to systems neuroscience, gene expression, posttranscriptional regulatory processes, to ecology, but also include societal and economic systems that have complex interdependencies. The processes that we are most interested in are those where the data has a particular geometry known as low dimensional manifolds. These are geometrical objects generated from embeddings of data that allows us to predict their future behaviors, investigate causal relationships, find if a system is becoming unstable, find early warning signs of critical transitions or catastrophes and more. Our computational approaches are based on tools that have their origin in the generalized Takens theorem, and are collectively known as empirical dynamic modeling (EDM). As a lab we are both a wet and dry lab where we design wet lab experiments that maximize the capabilities of our mathematical methods. The results from this data driven science approach then allows us to generate mechanistic hypotheses that can be again tested experimentally for empirical confirmation. This approach merges traditional hypothesis driven science and the more modern Data driven science approaches into a single virtuous cycle of discovery.
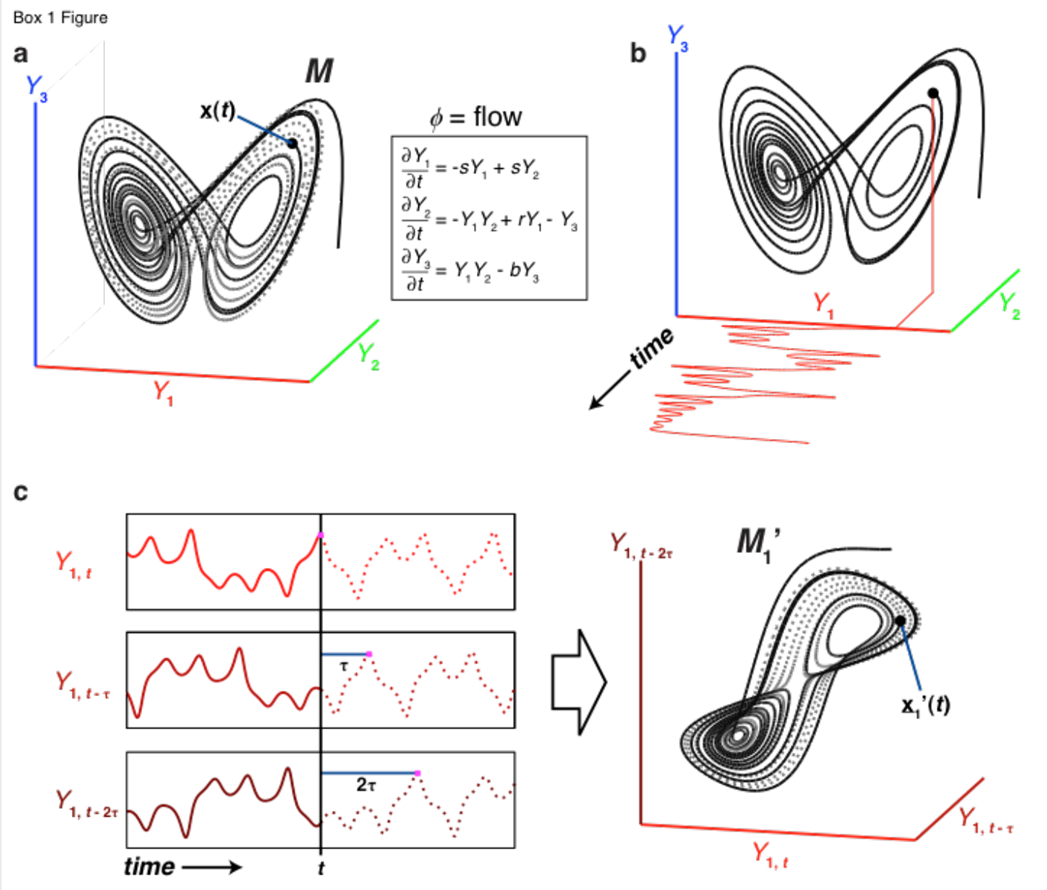
An Illustration of the Takens theorem. a) The Lorenz butterfly attractor example for the Takens theorem. The attractor manifold M is the set of states that the system progresses through. x(t) is the state of the system at time t, and the dynamics are defined by the Lorenz equations. b) A time series is simply a projection of the system states from M to a coordinate axis (Y1 is a state variable of the system). The manifold can be constructed from the component time series. c) Following Takens Theorem, lags of the time series {Y1} can act as coordinate axes to construct a shadow manifold M1’which maps 1:1 to the original manifold M (the visual similarity between M1’ and M is apparent). These shadow manifolds can be used for dynamics-based prediction of all kinds of systems, identifying causal variables, and much else.
Big Data Causal inference
Convergent cross-mapping is a powerful technique developed by George Sugihara for the causal inference of nonlinear systems. In our work we have adapted this computationally intensive method for high performance computing through software and hardware modifications to make it possible to be used for Big Data science applications. We actively collaborate with supercomputing centers throughout Japan and professors Keichi Takahashi (Tohoku University) on HPC and Hiroaki Natsukawa (Osaka Seikei University) on big data visualization applications. Applications are primarily for natural as well as human built systems that form large networks.
Downloading the Brain into computers
We have developed a new mathematical framework that allows us to convert observations of whole brain activity into a computational representation that reproduces both the behavior as well as the brain activity of experimental organisms such as flies and fish for which we have large scale brain recordings. The algorithm named Generative Manifold Networks essentially allows the downloading brains into computers using a network extended form of the generalized Takens theorem. We are extending this work to test the settings in which this algorithm works well and are developing an extension of this algorithm into new learning algorithms that start with a downloaded brain but is able to perform continual learning.
Causality without correlation
Although it is widely known that correlation does not guarantee causality, the converse the existence of causality without correlation is not well known in many areas, especially in biology. We are particularly interested in systems in which causality without correlation exists due to the fact that they are extremely nonlinear low dimensional systems. These systems exhibit behaviors akin to “perfect storms” where multiple conditions have to be met to integrate a particular outcome. We are particularly keen on studying systems like these in the epigenetics of pluripotency and neuroscience where we can verify the causality with experiments to proof such relationships.
Cephalopod proteins and collective behavior
Our unit also works on cephalopod specific genes and in particular reflectin proteins that have unusually high optical refractive indices and naturally form optically active nanoparticles. Using tools from human gene therapy we are developing reflectins into optical tools for microscopy and other materials science applications. In addition in collaboration with the Reiter and Miller units, we use tools from Data Science to study the social interactions between cephalopods and develop genetic tools for the study for systems neuroscience in cephalopods.