Code - Fujin - Validation - Non-Newtonian multiphase flow

Rotation of a spherical particle in a Non-Newtonian Couette flow

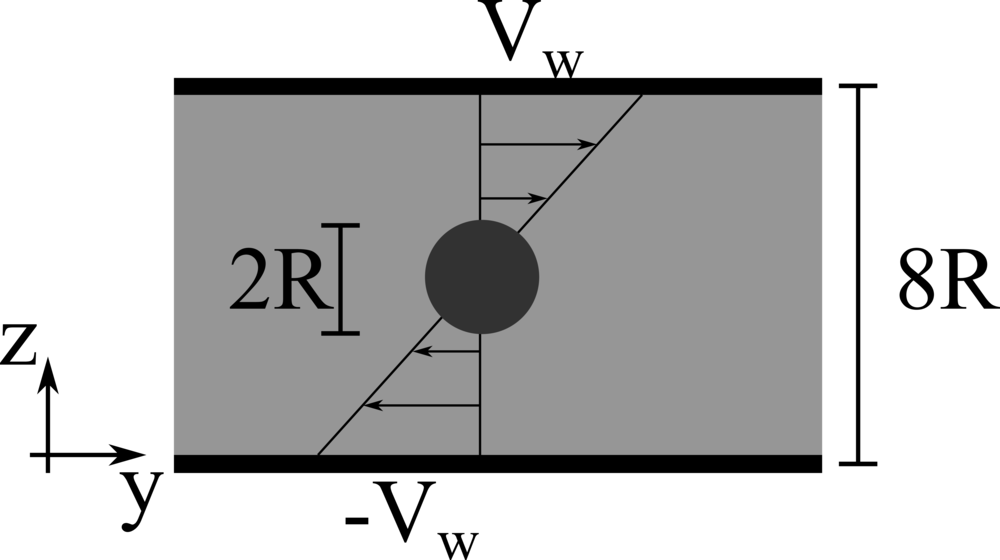
*Sketch of the computational domain and of the Cartesian coordinate system.*

We consider a spherical particle of radius \(R\) immersed in a Non-Newtonian elastic fluid. The computational domain has size \(4 R \times 8R \times 8R\) and is discretised with \(24\) grid points per particle diameter. The top and bottom walls move with opposite velocity \(\pm V_w\), providing a shear rate \(\dot{\gamma} = 2V_w/8R\), while periodic boundary conditions are imposed in the remaining directions. The particle is neutrally buoyant, and the Reynolds number \(Re = \rho \dot{\gamma} R^2 / \mu\) is fixed equal to \(0.025\). The fluid is modelled with the Oldroyd-B model and the Weissenberg number \(Wi = \lambda \dot{\gamma}\) is varied between \(0\) and \(2\).

config.h

#define _FLOW_COUETTE_
#define _SOLVER_FFT2D_
#define _MULTIPHASE_
#define _MULTIPHASE_NNF_
#define _MULTIPHASE_IBM_
#define _MULTIPHASE_VISCOSITY_UNIFORM_
#define _MULTIPHASE_DENSITY_UNIFORM_
#define _MULTIPHASE_NNF_OLB_
#define _MULTIPHASE_NNF_XXX_LOG_
#define _MULTIPHASE_IBM_3D_

param.f90

!Total number of grid points in X, Y and Z
integer, parameter :: nxt = 24*2, nyt = 24*4, nzt = 24*4
!Size of the domain in X, Y and Z
real, parameter :: lx = 2.0, ly = 4.0, lz = 4.0
!Fluid viscosity and density
real, parameter :: vis = 5.0, rho = 1.0
!Reference velocity (bulk velocity or wall velocity)
real, parameter :: refVel = 1.0
!Gravitational acceleration
real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/)
!Output frequency
integer,parameter :: iout0d = 500, iout1d = 1000000, iout2d = 1000000, iout3d = 1000000, ioutfld = 1000000
real, parameter :: nnVis=vis, nnLambda=4.0
integer, parameter :: ibmN=1
real, parameter :: ibmR = 0.5, ibmRho = rho, ibmRhoF = rho

main.f90

!Simulation initial step
iStart = 0
!Simulation final step
iEnd   = 9999999
!Choose the timestep
dt = 0.000001*32./24.

initPositionParticle.dat

1.0 2.0 2.0 0.5

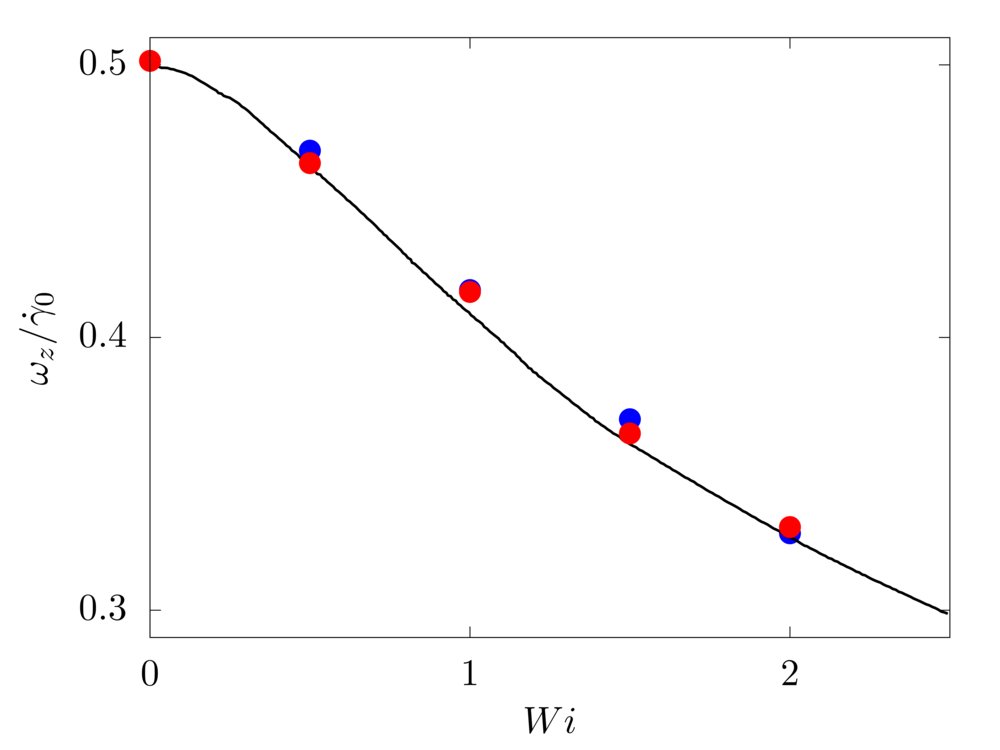
*Profiles of the ratio of the particle angular velocity to the applied shear rate as a function of*
*the Weissenberg number. The blue symbols denote the numerical results, the red symbols the experiments from Ref. [1] and the black line the numerical prediction from Ref. [2].*

References:

[1] F. Snijkers, G. D’Avino, P. L. Maffettone, F. Greco, M. A. Hulsen, and J. Vermant. Effect of vis- coelasticity on the rotation of a sphere in shear flow. Journal of Non-Newtonian Fluid Mechanics, 166(7-8):363–372, 2011.

[2] N. Goyal and J. J. Derksen. Direct simulations of spherical particles sedimenting in viscoelastic fluids. Journal of Non-Newtonian Fluid Mechanics, 183:1–13, 2012.