FY2022 Annual Report
Geometric Partial Differential Equations Unit
Associate Professor Qing Liu
Abstract
Our research centers on investigating the well-posedness and geometric properties of diverse nonlinear partial differential equations in various geometric contexts. Motivated by applications in surface evolutions, crystal growth, and image processing, we employ convex analysis techniques to study nonlinear nonlocal partial differential equations within the framework of viscosity solution theory. We extend the existing knowledge to encompass a broader class of PDEs, weaken the space structure to allow general geometric settings including sub-Riemannian manifolds, and thus largely expand the scope of applications. Furthermore, we also tackle nonlinear eigenvalue problems in general metric spaces and contribute to further development of PDE theory.
1. Staff
- Prof. Qing Liu, Group Leader
- Dr. Erbol Zhanpeisov, Postdoctoral Scholar
- Ms. Karabo Kwelegano, Rotation Student
- Ms. Wan Nur Syuhada binti Wan Suhaimi, Intern Student
- Ms. Yukiko Nakagawa, Administrative Assistant
2. Collaborations
2.1 Principal eigenvalue problem for infinity Laplacian in metric spaces
- Description: We consider the principal eigenvalue and eigenfunctions associated with the infinity Laplacian with homogeneous Dirichlet boundary condition in metric spaces. Our major contribution is a general framework that can be applied to study this eigenvalue problem in a large variety of metric spaces.
- Type of collaboration: Joint research
- Researchers:
- Qing Liu, OIST
- Ayato Mituishi, Fukuoka University
2.2 Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations
- Description: We investigate the preservation of spatial quasiconvexity of viscosity solutions to a general class of fully nonlinear nonlocal parabolic equations.
- Type of collaboration: Joint research
- Researchers:
- Takashi Kagaya, Muroran Institute of Technology
- Qing Liu, OIST
- Hiroyoshi Mitake, University of Tokyo
2.3 Horizontally quasiconvex envelope in the Heisenberg group
- Description: We establish a PDE approach to deal with a certain weak type of convexity for both sets and functions in the Heisenberg group. We provide a characterization for such convex sets and functions by adopting the viscosity solution theory for a nonlocal Hamilton-Jacobi equation.
- Type of collaboration: Joint research
- Researchers:
- Antoni Kijowski, OIST
- Qing Liu, OIST
- Xiaodan Zhou, OIST
2.4 Existence for time fractional semilinear parabolic equations
- Description: We study the existence of solutions to time-fractional parabolic equations. Instead of the usual decay estimates in Lebesgue spaces for time-fractional power equations, we use decay estimates in Besov-Morrey spaces to give a new existence result.
- Type of collaboration: Joint research
- Researchers:
- Yusuke Oka, University of Tokyo
- Erbol Zhanpeisov, OIST
3. Activities and Findings
3.1 Principal eigenvalue problem for infinity Laplacian in metric spaces
We study the Dirichlet eigenvalue problem associated with the infinity Laplacian in metric spaces. We establish a direct partial differential equation approach to find the principal eigenvalue and eigenfunctions in a proper geodesic space without assuming any measure structure. The key step in our work is to find an appropriate notion of solutions. We show the existence of solutions of the eigenvalue problem by adapting Perron’s method. Our method is different from the standard limit process via the variational eigenvalue formulation for p-Laplacian in the Euclidean space. Note that the simplicity of the eigenvalue for infinity Laplacian is a long standing open question. We discuss this problem in the setting of metric graphs and provide an example, as below, showing that eigenfunctions are in general not unique up to multiplicative constants without adding sufficient constraints.
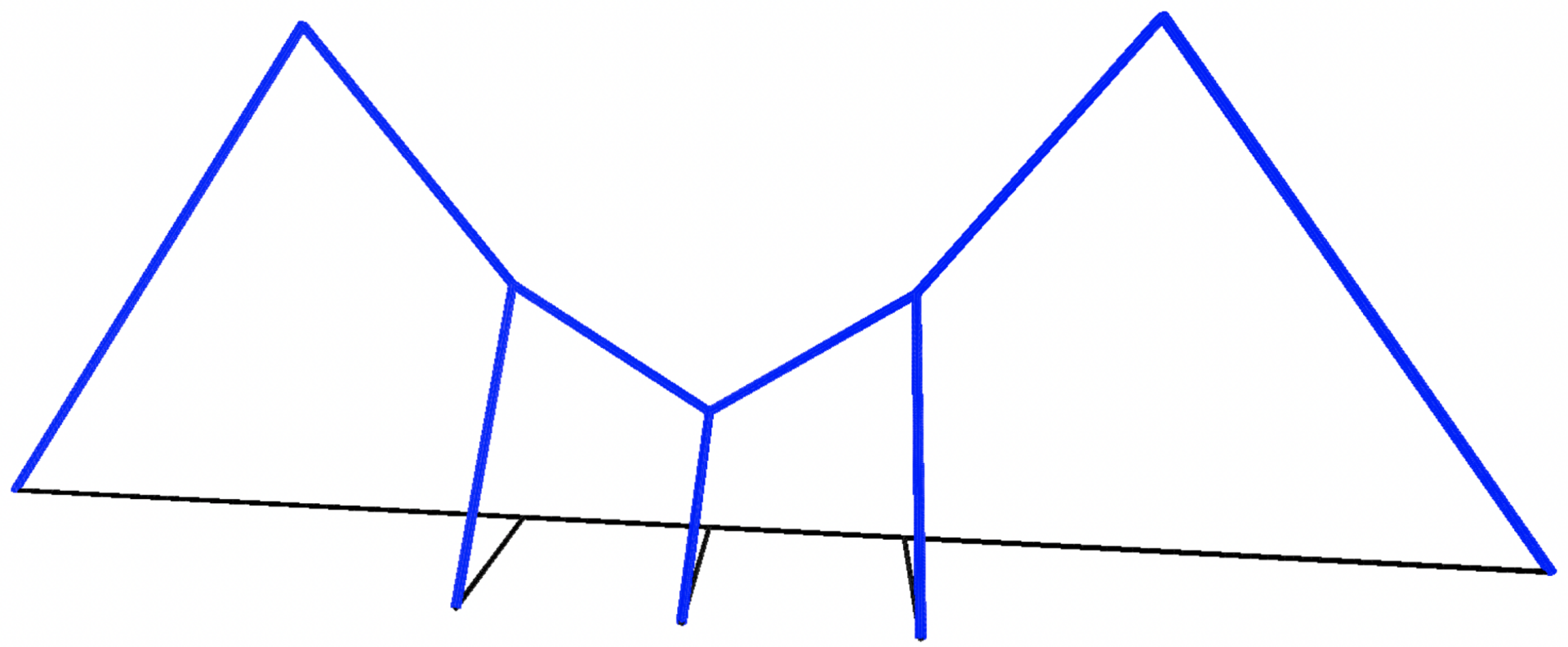

3.2 Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations
This work is concerned with a general class of fully nonlinear parabolic equations with monotone nonlocal terms. We investigate the quasiconvexity preserving property of positive, spatially coercive viscosity solutions. We prove that if the initial value is quasiconvex, the viscosity solution to the Cauchy problem stays quasiconvex in space for all time. Our proof can be regarded as a limit version of that for power convexity preservation as the exponent tends to infinity. Our result is not only applicable to a general class of level set nonlocal geometric equations but also allows the parabolic operator to additionally depend on the unknown.
3.3 Horizontally quasiconvex envelope in the Heisenberg group
We propose a PDE-based approach to the horizontally quasiconvex (h-quasiconvex for short) envelope of a given continuous function in the Heisenberg group. We provide a characterization for upper semicontinuous, h-quasiconvex functions in terms of the viscosity subsolution to a first-order nonlocal Hamilton-Jacobi equation. We also construct the corresponding envelope of a continuous function by iterating the nonlocal operator. One important step in our arguments is to prove the uniqueness and existence of viscosity solutions to the Dirichlet boundary problem for the nonlocal Hamilton-Jacobi equation. Applications of our approach to the h-convex hull of a given set in the Heisenberg group are discussed as well.
4. Publications
4.1 Journals
- Kijowski, A., Liu, Q., Zhou, X., Horizontally quasiconvex envelope in the Heisenberg group, to appear in Rev. Mat. Iberoam.
- Liu, Q., Zhou, X., Differential games and Hamilton-Jacobi-Isaacs equations in metric spaces, Minimax Theory Appl., 8 (2023), 121-138.
- Kagaya, T., Liu, Q., Mitake, H., Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations, NoDEA Nonlinear Diffferential Equations Appl., 30 (2023), Paper No. 13. doi: 10.1007/s00030-022-00818-8
- Liu, Q., Mitsuishi, A., Principal eigenvalue problem for infinity Laplacian in metric spaces, Adv. Nonlinear Stud., 22 (2022), 548-573. doi:10.1515/ans-2022-0028
- Zhanpeisov, E., Existence of solutions to fractional semilinear parabolic equations in Besov-Morrey spaces, arXiv: 2301.04236.
- Oka, Y., Zhanpeisov, E., Existence of solutions for time fractional semilinear parabolic equations in Besov-Morrey spaces, arXiv: 2305.05969.
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Liu, Q., Principal eigenvalue problem for infinity Laplacian in metric spaces, University of Cincinnati Analysis Seminar, University of Cincinnati, Cincinnati, USA, February 23, 2023.
- Liu, Q., Horizontal quasiconvex functions in the Heisenberg group, Hiroshima Mathematical Analysis Seminar, Hiroshima University, Hiroshima, Japan, February 3, 2023.
- Liu, Q., Principal eigenvalue problem for infinity Laplacian in metric spaces, NLPDE seminar, Kyoto University, Kyoto, Japan, November 25, 2022.
- Liu, Q., Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations, RIMS Workshop on Innovation of the Theory for Evolution Equations: Developments via Cross-disciplinary Studies, RIMS, Kyoto University, Kyoto, Japan, October 18, 2022.
- Liu, Q., Convexity in Partial Differential Equations, OIST Faculty Lunchtime Seminar, October 12, 2022.
- Liu, Q., Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations, Asia-Pacific Analysis and PDE Seminar (online), October 3, 2022.
- Liu, Q., Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations, Conference on Systematical Geometric Analysis and Asymptotic Analysis for Evolution Equations, University of Tokyo, Tokyo, Japan, August 2, 2022.
- Liu, Q., Principal eigenvalue problem for infinity Laplacian in metric spaces, Conference on Theoretical and Numerical Trends in Inverse Problems and Control for PDE’s, and Hamilton-Jacobi Equation, CIRM at Luminy, Marseille, France, June 14, 2022.
- Liu, Q., Quasiconvexity preserving property for fully nonlinear nonlocal parabolic equations, Waseda University Applied Analysis Seminar, Tokyo, Japan, June 4, 2022.
- Zhanpeisov, E., Existence of solutions for fractional semilinear parabolic equations in Besov-Morrey spaces, OIST Conference Geometric PDEs and Applications, January 18, 2023.
5. Intellectual Property Rights and Other Specific Achievements
Nothing to report
6. Meetings and Events
6.1 Geometric PDE and Applied Analysis Seminar
- Oct. 13, 2022
- Speaker: Mikko Parviainen (University of Jyväskylä)
- Title: Stochastic tug-of-war type games and partial differential equations
- Oct. 27, 2022
- Speaker: Kazuhiro Kuwae (Fukuoka University)
- Title: Liouville theorem for V-harmonic maps under non-negative (m, V)-Ricci curvature for non-positive m
- Nov. 10, 2022
- Speaker: Agnid Banerjee (TIFR CAM Bangalore)
- Title: Space like strong unique continuation for some fractional parabolic equations
- Nov. 17, 2022
- Speaker: Robert V. Kohn (New York University)
- Title: Prediction with expert advice: a PDE perspective on a model problem from machine learning
- Dec. 1, 2022
- Speaker: Shigeaki Koike (Waseda University)
- Title: ABP maximum principle with upper contact sets for fully nonlinear elliptic PDEs
- Dec. 1, 2022
- Speaker: Michiaki Onodera (Tokyo Institute of Technology)
- Title: A perturbation theory of overdetermined problems
- Dec. 15, 2022
- Speaker: Bernd Kawohl (University of Cologne)
- Title: On Reuleaux and Cohn-Vossen, or buttons and balls that cannot run away
6.2 OIST Workshop Analysis on Metric Spaces
- Date: May 23-27, 2022
- Venue: OIST Conference Center
- Co-organizers: Luca Capogna (Smith College), Qing Liu (OIST), Shin-ichi Ohta (Osaka University), Nageswari Shanmugalingam (University of Cincinnati), Xiaodan Zhou (OIST)
- Speakers:
- Hiroaki Aikawa (Chubu University)
- Luigi Ambrosio (SNS Pisa)
- Mario Bonk (University of California, Los Angeles)
- Luca Capogna (Smith College)
- Estibalitz Durand-Cartagena (Universidad Nacional de Educación a Distancia)
- Sylvester Eriksson-Bique (University of Oulu)
- Nicola Gigli (SISSA)
- Piotr Hajlasz (University of Pittsburgh)
- Shouhei Honda (Tohoku University)
- Yoshito Ishiki (RIKEN)
- Jun Kigami (Kyoto University)
- Riikka Korte (Aalto University)
- Pekka Koskela (University of Jyväskylä)
- Panu Lahti (Chinese Academy of Sciences)
- Andrea Mondino (University of Oxford)
- Shin-ichi Ohta (Osaka University/RIKEN)
- Nageswari Shamugalingam (University of Cincinnati)
- Karl-Theodor Sturm (University of Bonn)
- Short talk speakers
- Zhangkai Huang (Tohoku University)
- Kohei Sasaya (Kyoto University)
- Ryosuke Shimizu (Kyoto University)
- Hiroshi Tsuji (Osaka University)
6.3 OIST Conference Geometric PDEs and Applications
- Date: January 16-18, 2023
- Venue: OIST C209
- Co-organizers: Qing Liu (OIST), Hiroyoshi Mitake (University of Tokyo), Xiaodan Zhou (OIST)
- Speakers:
- Goro Akagi (Tohoku University)
- Jiwoong Jang (University of Wisconsin, Madison)
- Tianling Jin (Hong Kong University of Science and Technology)
- Inwon Kim (University of California, Los Angeles)
- Shuhei Kitano (Waseda University)
- Olivier Ley (IRMAR, INSA-Rennes)
- Adam Oberman (McGill University)
- Norbert Pozar (Kanazawa University)
- Julio Rossi (University of Buenos Aires)
- Hung Tran (University of Wisconsin, Madison)
- Shuntaro Tsubouchi (University of Tokyo)
- Yifeng Yu (University of California, Irvine)
- Erbol Zhanpeisov (OIST)
7. Other
Nothing to report.



