FY2014 Annual Report
Mathematical Biology Unit
Associate Professor Robert Sinclair

Abstract
We were able to celebrate a number of successes (such as Dr. Inoue winning on Open Science Award for his website) this year, but I would like to begin with the publication of work done by an intern, Haozhe Zhang, who showed what can be done in a few months if one has loads of curiosity, a very strong work ethic and the ability to switch between focusing on details and considering the big picture. Congratulations Haozhe! Work on a dinosaur bone was also finally published, after several years of work. The project raised a number of questions relating to the meaning of statistical analysis when not only sample sizes are small, but also sources of error are difficult to quantify (I am talking about broken and deformed fossilized bones), leading to a number of interesting challenges. I hope to return to some of these biologically relevant statistical questions in the future. Finally, two shorter papers explored the nature of the interface between mathematics and biology, one involving the mathematical analysis of a model to reach a biologically relevant conclusion, and the other returning to the roots of mathematics (music and the rational numbers) in the hope of finding new connections between numbers and modes of development. Dr. Inoue and I continue to work on the teleost–specific whole genome duplication.
1. Staff
- Dr. Jun Inoue, Staff Scientist
- Shino Fibbs, Administrative Assistant
2. Collaborations
- Theme: Theoretical Virology
- Researchers:
- Professor Dennis Bamford, University of Helsinki
- Dr. Janne Ravantti, University of Helsinki
- Researchers:
- Theme: Genome Evolution
- Type of collaboration: JSPS Grant 24770070
- Researchers:
- Professor Mutsumi Nishida, University of the Ryukyus
- Assistant Professor Yukuto Sato, Tohoku University
- Theme: Integrable Systems
- Researchers:
- Professor Martin Guest, Waseda University
- Associate Professor Takashi Sakai, Tokyo Metropolitan University
- Researchers:
3. Activities and Findings
3.1 Namibian Fairy Circles (Zhang and Sinclair)
Haozhe Zhang came as an intern from China, and expressed an interest in stochastic geometry. Through discussions with Prof. Masai here at OIST, I had become aware of very beautiful theoretical work which suggested that epithelial (think of skin) cells, from flies to humans, tend to form sheets with very distinctive patterns of connectivity. I wondered whether this was primarily due to the competition for space between cells, and whether this same theory could apply at macroscopic scales, so I asked Haozhe to work on satellite images of Namibian fairy circles (large, barren circles in an arid environment otherwise characterised by low grasses), to see whether similar patterns could be identified. The cause of Namibian fairy circles is still a mystery, but there are good reasons to expect that they are produced by biological entities (ants, termites, plant root systems etc.) which are very likely to be competing for resources, and, therefore, space.
Technically, the work was quite difficult, but Haozhe put his considerable skills and ingenuity to work, and managed to extract the relevant data from the images. Much to our surprise and delight, it was a perfect match!
The importance of this result is that it strongly suggests that types of pattern observed microscopically can also be observed in the large, and this in turn suggests that the same theory may apply. We hypothesize that Namibian fairy circle patterns may also reflect competition for space, and that our result may be demonstrating that mathematical analyses developed for microscopic systems may also apply to large systems (and vice-versa). Theoretically, this is a very exciting prospect!

Publishing the work was an uphill climb, given that both the approach and the result are so unusual. The response of one journal was
It is unclear why an attempt has been made to demonstrate the similarity in patterning between epithelial cells and Namibian fairy circles, or what it might mean that there are similarities. It seems difficult to draw any meaningful interpretation of the results. The authors state that value of their results is in demonstrating that a descriptive approach to the microscopic world can also be used to describe the macroscopic world, but do not make a convincing case for why one would want to do that or what one learns by doing so.
A reviewer response from a different journal was even more blunt:
What harm can there be in putting this idea out in the market place of ideas? On the other hand, I have seen erroneous ideas take hold and become resistant to purging, simply because the ideas were so appealing and "made sense" (the most dangerous phrase in science).
Happily, we did finally find a journal which understood that our work was quite serious. At OIST, we try to push the cutting edge of research, and this often involves working in unconventional ways (working "out of the box"), but truly new ideas are not always readily accepted by the scientific community.
Interestingly, the story was also picked up by the international press, and covered in more than ten countries in at least eight languages. It has also already been cited in the scientific literature.
3.2 Evolutionary Genomics of Vertebrates (Inoue & Sinclair)
All extant vertebrates experienced ancient whole genome duplication (WGD) events during their evolutionary history (Fig.1, vertebrate genome duplication [VGD] 1/2 and/or teleost genome duplication [TGD]). Therefore, these events are considered to have had a major impact on genomic architecture and consequently organismal features of vertebrates. In order to understand the evolution of vertebrate genomes, we are focusing on the fish-specific WGD, what is known as TGD, for the following reasons: 1) more evidence remains from the TGD than from the other older events for evolutionary study and 2) a time-calibrated tree combining molecular and fossil evidence can be used to trace the teleost diversification pattern.
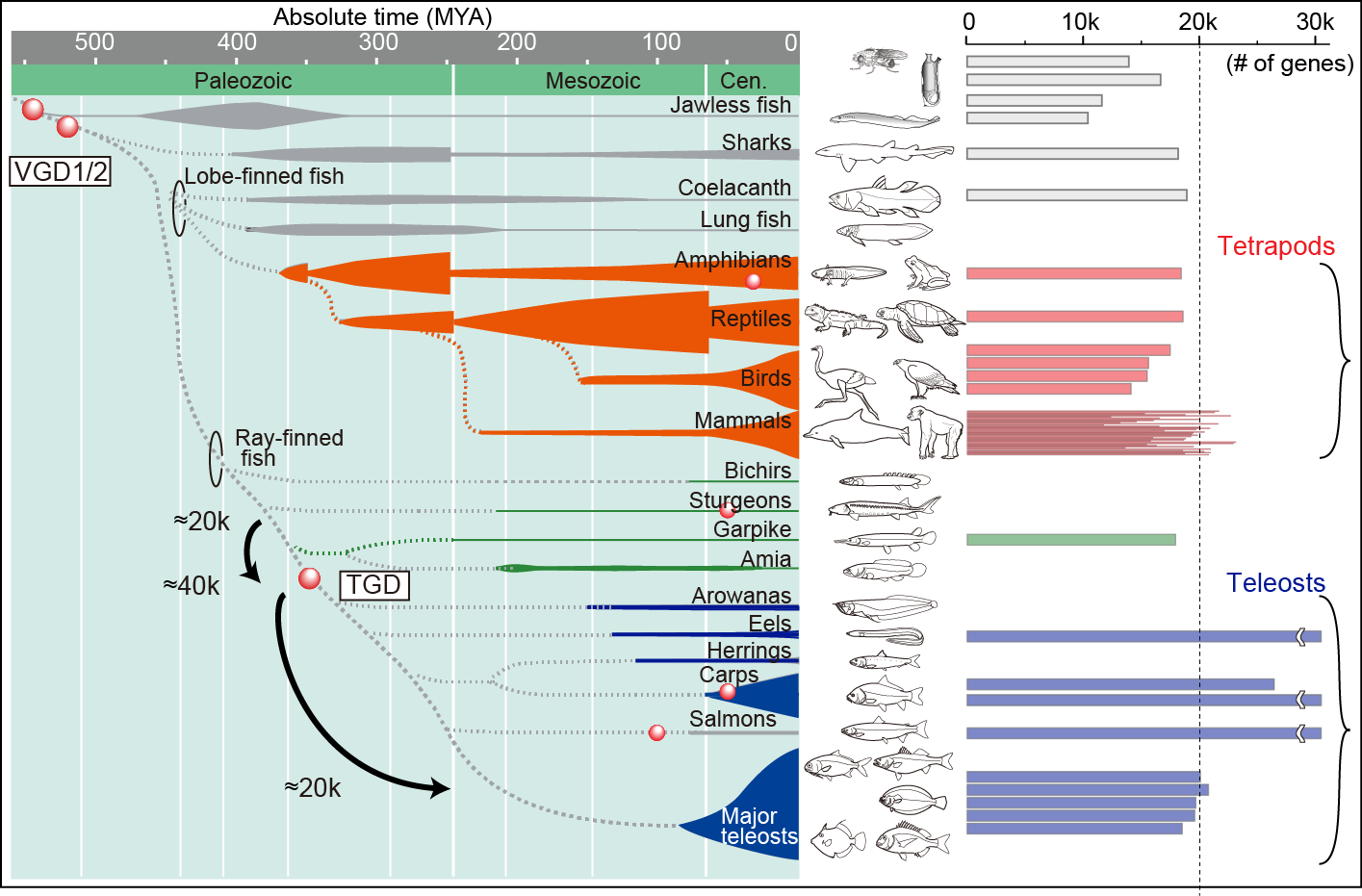
Considering that the numbers of protein-coding genes are almost the same among tetrapods and teleosts (Fig. 1, ca. 20k), all genes duplicated by TGD are thought to revert in number over teleost history. Therefore, genome reorganizations accompanied by gene loss events are considered to play a key part in shaping teleost characteristics (e.g., ecological and morphological diversity). We explored the link between the genome organization and the teleost evolution with mathematical modeling.
Analysis pipeline (Inoue): Reliable orthology information is crucial for comparative genome analysis. However, variable gene loss/persistence pattern among teleost species after TGD makes the identification of orthologs and TGD-derived paired genes difficult. In order to identify reliable orthologs among tetrapods and teleosts, we constructed phylogeny-based pipeline (Fig. 2). As a result, we successfully identified ca. 7,000 sets of orthologs by analyzing all protein-coding gene sequences of 17 animals. The orthology information will be distributed from our website of the Orthology Database of Fish Specific-WGD derived Genes (Fig. 3).
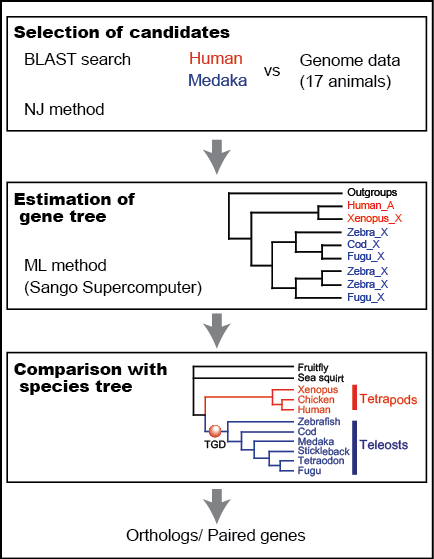
Spatiotemporal gene loss pattern: In order to estimate genomic positional and temporal (spatiotemporal) loss pattern of TGD-derived gene pairs, evolutionary analyses were conducted along with the time-calibrated tree using the results obtained from the pipeline. The genomic positional patterns of gene loss were estimated by comparing ortholog arrangements among species and the temporal patterns were reconstructed by estimating the number of remaining gene pairs in each ancestral and extant species. These results clarified the timing of gene loss and genome reorganization after TGD.
Mechanism of gene loss: In order to understand the mechanisms of gene loss after TGD, the observed temporal pattern of gene loss was fitted by several gene-loss models. The fitting analysis has allowed us to propose a possible mechanism of the observed gene loss pattern after TGD. By integrating the results obtained above, we have been able to discuss interrelationships between the genome reorganization and species diversification of teleosts.
Most of the year was spent on the manuscript describing this work, which has since been accepted by a prestigious journal. Please watch this space!
3.3 Dinosaurs! (Sinclair)
The eminent British anatomist Richard Owen, who first introduced the term "dinosaur", was said to have been able to identify an animal from a single bone. I was contacted by palaeontologists (Dr. Tom Rich of Museum Victoria, Australia, and others), who were in the difficult situation of having a single bone which was attracting controversy. The reason was that it seemed to be from a type of dinosaur which should never have been in Australia at all, given that this type is commonly thought to have originated in a different part of the world which has not been connected to Australia by a land bridge at any time since then. The size of the bone made it clear that it was not likely to have been an animal which could have been transported by air or sea, and some controversy had developed, with some palaeontologists flatly refusing to believe that this bone could be what it seemed to be.
I was initially asked to assist with statistical analysis, but soon discovered that far more was required, since many of the length and width measurements necessary for the analysis had been done to an unsatisfactory precision. This meant combing through the paleontological literature for accurate, scaled images of fossil bones and also taking measurements directly from museum specimens (I have Dr. Makoto Manabe to thank for access to specimens held by the National Museum of Nature and Science in Tokyo). Finally, it turned out to be possible to address some of the more serious issues relating to sources of error, by carefully considering pairs of bones known to have once belonged to individual animals (as left and right forearms), and to include this in the mathematical analysis.
Since so few dinosaurs are known to have lived in Australia, this one was included in an Australia Post stamp set, based upon the following picture (reproduced here with permission):

It is wonderful to see how mathematics can contribute to our understanding of the distant past!
3.4 Rational Numbers and Development? (Sinclair)
Modern (Western or European) mathematics is considered to have originated in ancient Greece, with Pythagoras and his followers, who believed that rational numbers (such as "one half" or "three fifths") had a connection with music, and were thought of in an almost religious sense. Since that time, while we no longer regard these numbers as having any mystical power or meaning, it has often been the case that the discovery of simple fractions has pointed to the existence of underlying laws. This is true in chemistry, for example. Also, Mendel's laws are very much based upon simple ratios. The point is that even very complex processes sometimes reveal hidden regularities in the form of simple ratios.
There are some well-known cases in developmental biology where patterns are extremely well ordered (the compound eyes of a fly, for example), and also some where seemingly random patterns emerge. Are the former in any way related to simple rational numbers, and the latter not? I wrote a paper about this, suggesting that there may in fact be a link, even if it is not a law (i.e. there can be exceptions). This is a topic I hope to spend more time on in the future, and I intend to visit some experimental groups in order to learn more about modes of development.
3.5 Persistence of Sensitive Strains in the presence of Killer Strains (Sinclair)
Microbes are often engaged in very sophisticated conflict with each other. One strategy is to produce a toxin which can kill other microbes, but for which the producer has immunity. This is observed in some strains of yeast, for example. What is observed in the wild is that killer strains and sensitive strains, which have no defense at all, often co-exist, although one would imagine that the killers could simply wipe out the others. Also, there does not always appear to be any difference in growth rates between killer and sensitive strains.
I looked at this from a theoretical point of view. Theory would usually predict that co-existence is not possible unless the sensitives could reproduce fast enough to replace the numbers lost to the killers, usually thought to require much higher growth rates for sensitive strains as compared to the killers. Observations are suggesting that is not what actually happens. I asked whether one could construct any type of model for which co-existence would be possible, even if the differences in growth rates were negligible.
The result was that it is indeed possible. This was an unusual project, since mathematical analysis was performed on a mathematical model using techniques usually reserved for pure mathematical analysis. I am happy to see that the line between so-called pure and applied mathematics does not actually exist: I believe that mathematics will be enriched by engaging with biology, and that types of mathematics we currently think of as "pure" will in fact turn out to be very applicable!
4. Publications
4.1 Journals
- Rich, T. H., Kear, B.P., Sinclair, Robert., Chinnery, B., Carpenter, K., McHugh, M.L., Vickers-Rich, P. Serendipaceraptops arthurcclarkei Rich & Vickers-Rich, 2003 is an Australian Early Cretaceous ceratopsian. Alcheringa: An Australasian Journal of Palaeontology, doi:10.1080/03115518.2014.894809 (2014)
- Sinclair, Robert. Persistence in the shadow of killers. Frontiers in Microbiology, doi:10.3389/fmicb.2014.00342 (2014)
- Sinclair, Robert. Do rational numbers play a role in selection for stochasticity? Frontiers in Computational Neuroscience, doi:10.3389/fncom.2014.00113 (2014)
- Zhang, Haozhe., Sinclair, Robert. Namibian fairy circles and epithelial cells share emergent geometric order. Ecological Complexity, doi:10.1016/j.ecocom.2015.02.001 (2015)
4.2 Books and other one-time publications
Nothing to report
4.3 Oral and Poster Presentations
- Sinclair, Robert. Geometry before Euclid: How Life Explored and Conquered the Dimensionality of 3-Space, iTHES Theoretical Science Colloquium, RIKEN iTHES, Wako, Saitama, Japan, (2014)
- Inoue, Jun. Bayesian divergence time estimation. Theory and practical training of molecular phylogenetics AFFRIT Workshp No.176, Tsukuba, Japan, (2014)
- Sinclair, Robert. The Mathematics of Hiking, Bracelets and DNA. OIST Open Campus (2015)
- Sinclair, Robert. Geometry before Euclid. Okinawa Prefectural Museum & Art Museum (2015)
5. Intellectual Property Rights and Other Specific Achievements
5.1 Dr. Inoue Wins Open Science Award
Dr. Jun Inoue, a staff scientist of the Mathematical Biology Unit at the Okinawa Institute of Science and Technology Graduate University (OIST), has received one of this year’s Open Science Awards (Category: Website) for his website of evolutionary analysis (http://www.geocities.jp/ancientfishtree/index_eng.html).
http://2014.openscienceaward.org
6. Meetings and Events
6.1 A butterfly effect: crystallographic phyllotaxy II
- Date: June 3, 2014
- Venue: OIST Campus Lab1
- Speaker: Dr. Iain Aitchison (The University of Melbourne)
6.2 Fossils from Gabon show early steps toward multicellularity and the oldest biodiversity 2.1 billion years ago: A new chapter of Life history
- Date: November 5, 2014
- Venue: OIST Campus Lab1
- Speakers: Prof. Abderrazak El Albani (The University of Poitiers)
6.3 Why do freshwater eels migrate thousands kilometers in oceans?
- Date: February 24, 2015
- Venue: OIST Campus C209
- Speakers: Prof. Katsumi Tsukamoto (Nihon University)
7. Other
Nothing to report.



