Code - Fujin - Validation - Immersed Boundary Method
Uniform flow around a cylinder
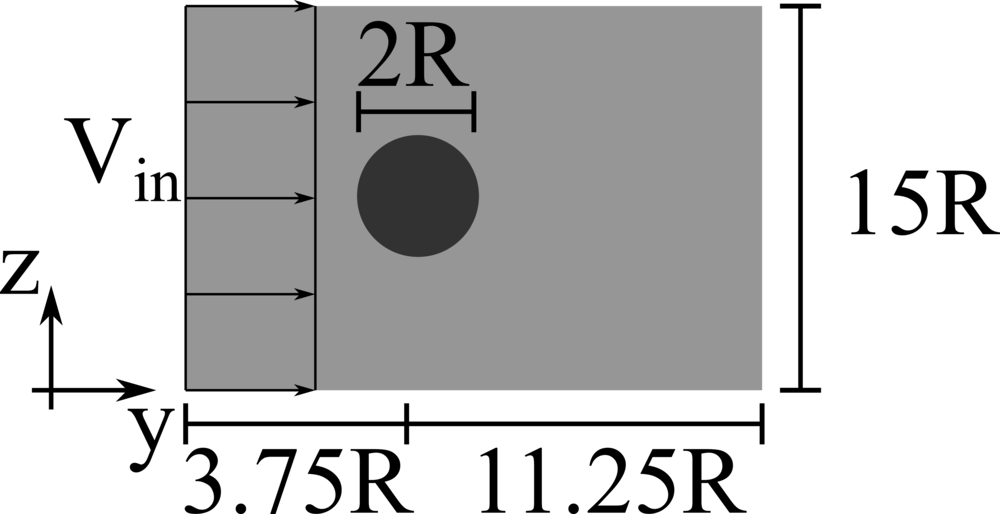
We consider a 2D rigid cylinder of radius R located in a computational domain of size \(15R \times 15R\), discretised with a resolution of \(68\) grid points per particle diameter. The incoming flow is uniform with velocity \(V_{in}\), providing a Reynolds number \(Re = D V_{in}/\nu\) of \(100\), \(150\) and \(200\).
config.h
#define _FLOW_COUETTE_ #define _FLOW_INOUT_ #define _FLOW_INOUT_UNBOUND_ #define _SOLVER_INOUT_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 2048, nzt = 2048 ! Size of the domain in X, Y and Z real, parameter :: lx = 30.0/2048.*4., ly = 30.0, lz = 30.0 ! Fluid viscosity and density real, parameter :: vis = 1.0/200.0 real, parameter :: rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) ! Number of particles integer, parameter :: ibmN = 1 ! Particle radius and density real, parameter :: ibmR = 0.5, ibmRho = 1.0, ibmRhoF = rho
input/input.in
# Simulation initial and final step 1200000 9999999 # Simulation time 299.99999999463392 # Simulation time-step 2.5000000000000001E-004 # Output frequency 400 1000000 40000 1000000 400000 # Simulation restart condition for the multiphase part F
initParticlePosition.dat
7.5 15.0

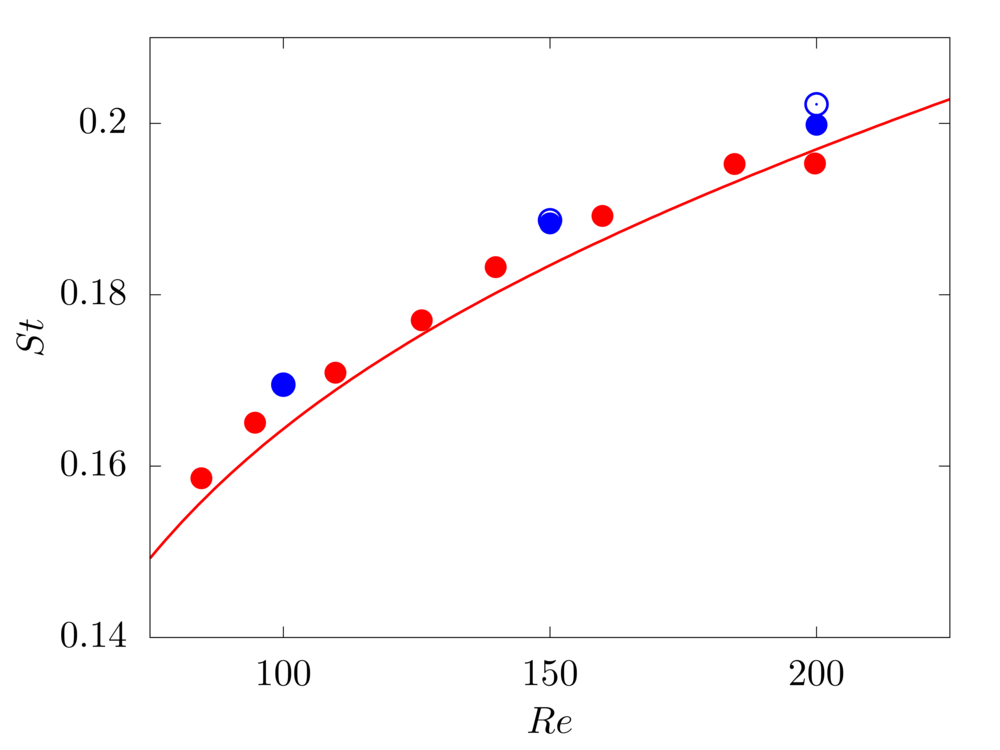
Lateral migration of a circular cylinder in a shear flow
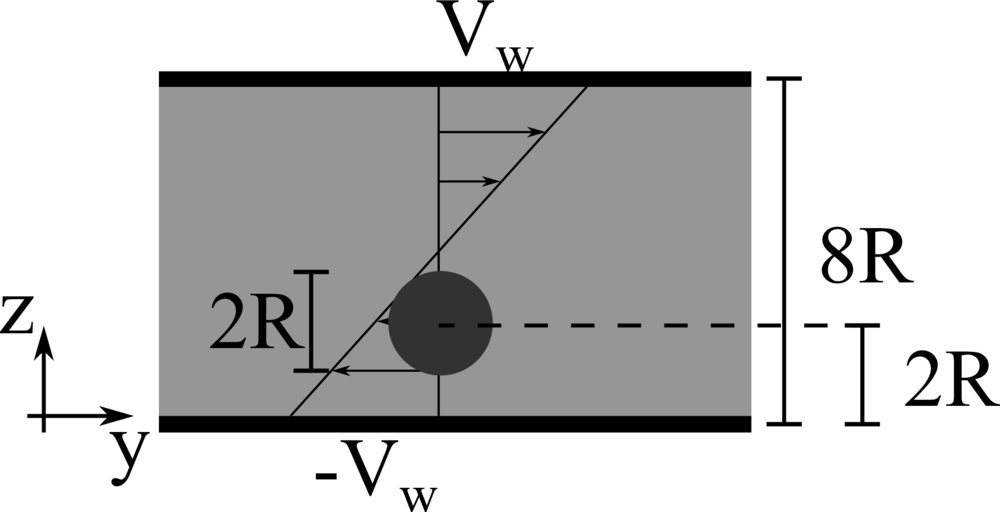
We consider a 2D rigid cylinder of radius R located in a computational domain of size \(8R \times 50R\), discretised with a resolution of \(16\) grid points per particle diameter. The top and bottom walls move with opposite velocity \(\pm V_w\), providing a shear rate \(\dot{\gamma} = 2 V_w/8R\), while periodic boundary conditions are imposed in the remaining directions. The particle is neutrally buoyant, and the Reynolds number \(Re = \rho \dot{\gamma} R^2 / \mu\) is fixed equal to \(40\). Two different initial conditions are studied: \(z = 2R\) and \(6R\).
config.h
#define _FLOW_COUETTE_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 8*50, nzt = 8*8 !Size of the domain in X, Y and Z real, parameter :: lx = 4.0/8.0, ly = 50.0, lz = 8.0 !Fluid viscosity and density real, parameter :: vis = 1.0*8.0/40.0, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.5 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 4000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR=1.0, ibmRhoF=rho, ibmRho=ibmRhoF, ibmVol=pi*ibmR**2, ibmMas=ibmRho*ibmVol, ibmIne=0.5*ibmMas*ibmR**2
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.000001
initParticlePosition.dat
0.5 2.0
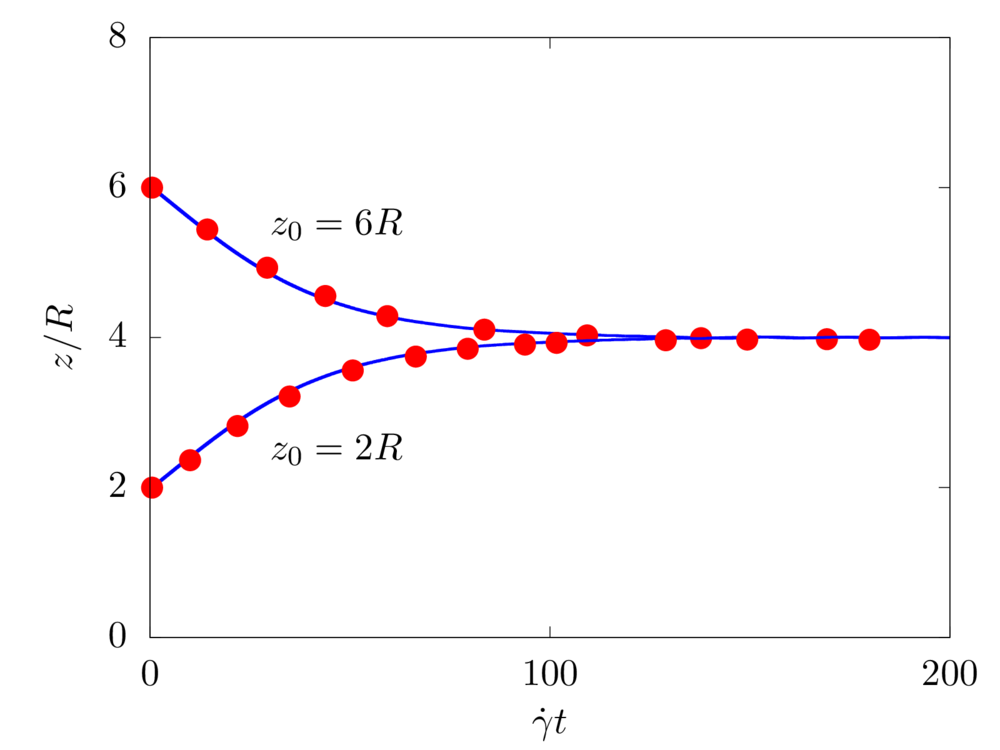
Lateral migration of a circular cylinder in a pressure driven flow
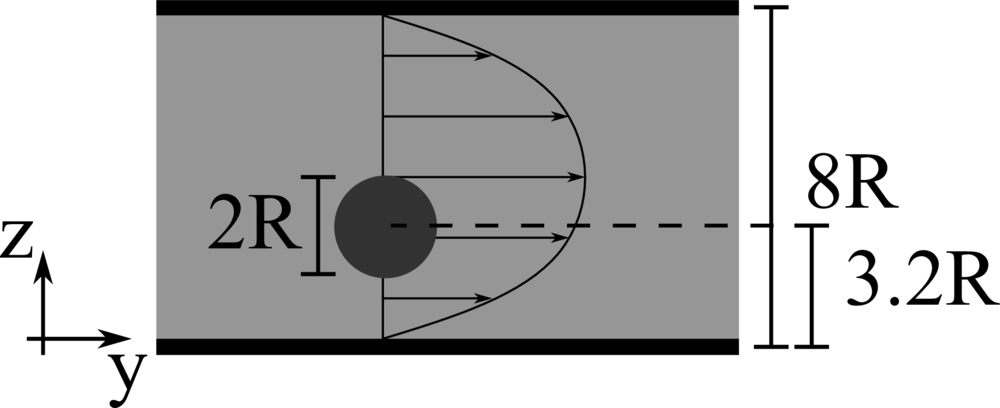
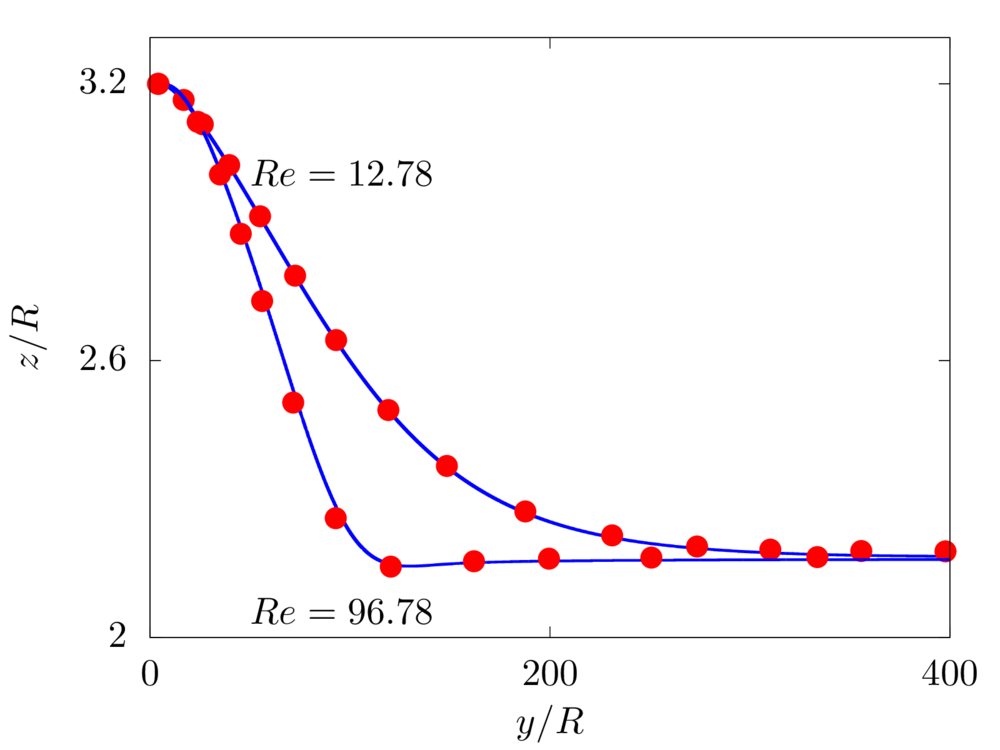
We consider a 2D rigid cylinder of radius R located in a computational domain of size \(8R \times 8R\), discretised with a resolution of \(32\) grid points per particle diameter. The flow is driven by an imposed pressure gradient, such that the resulting Reynolds number \(Re = \rho V_b 8R/\mu\) is equal to \(12.78\) and \(96.74\). The particle is neutrally buoyant and initially located at \(3.2R\) from the bottom wall.
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 256, nzt = 256 !Size of the domain in X, Y and Z real, parameter :: lx = 1.0/128.0*4.0/2.0, ly = 1.0, lz = 1.0 !Fluid viscosity and density real, parameter :: vis = 4.283E-04, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.0 !Imposed pressure gradient real, parameter :: gradP = 2.337E-04 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 4000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR=0.125, ibmRhoF=rho, ibmRho=ibmRhoF, ibmVol=pi*ibmR**2, ibmMas=ibmRho*ibmVol, ibmIne=0.5*ibmMas*ibmR**2
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.001
initParticlePosition.dat
0.5 0.4
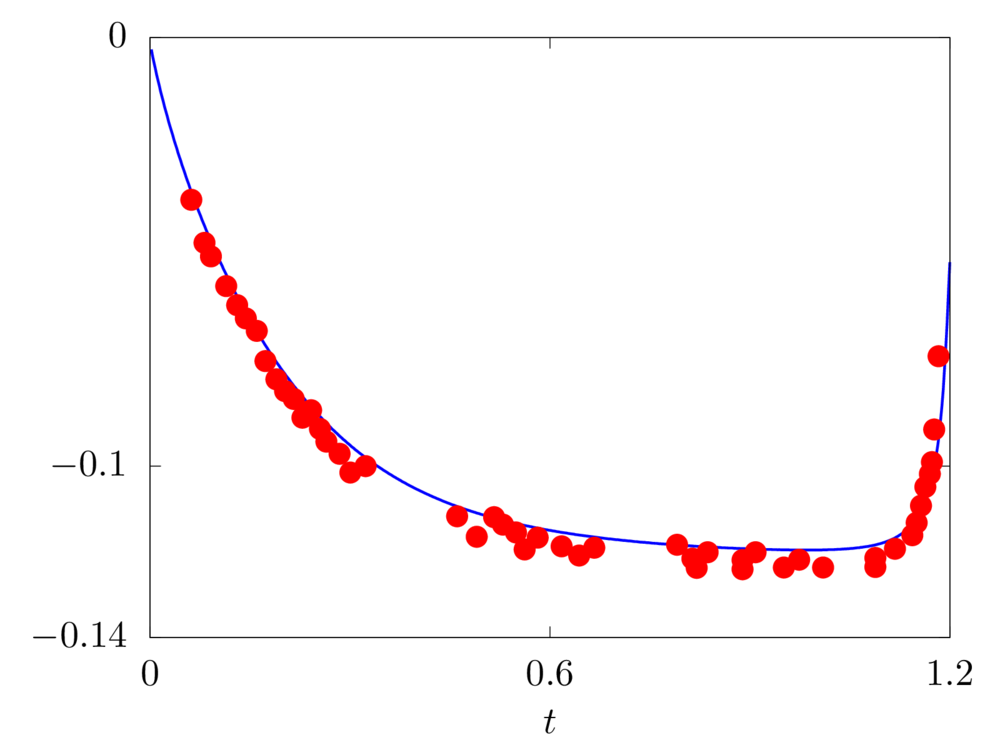
Sedimentation of a spherical particle
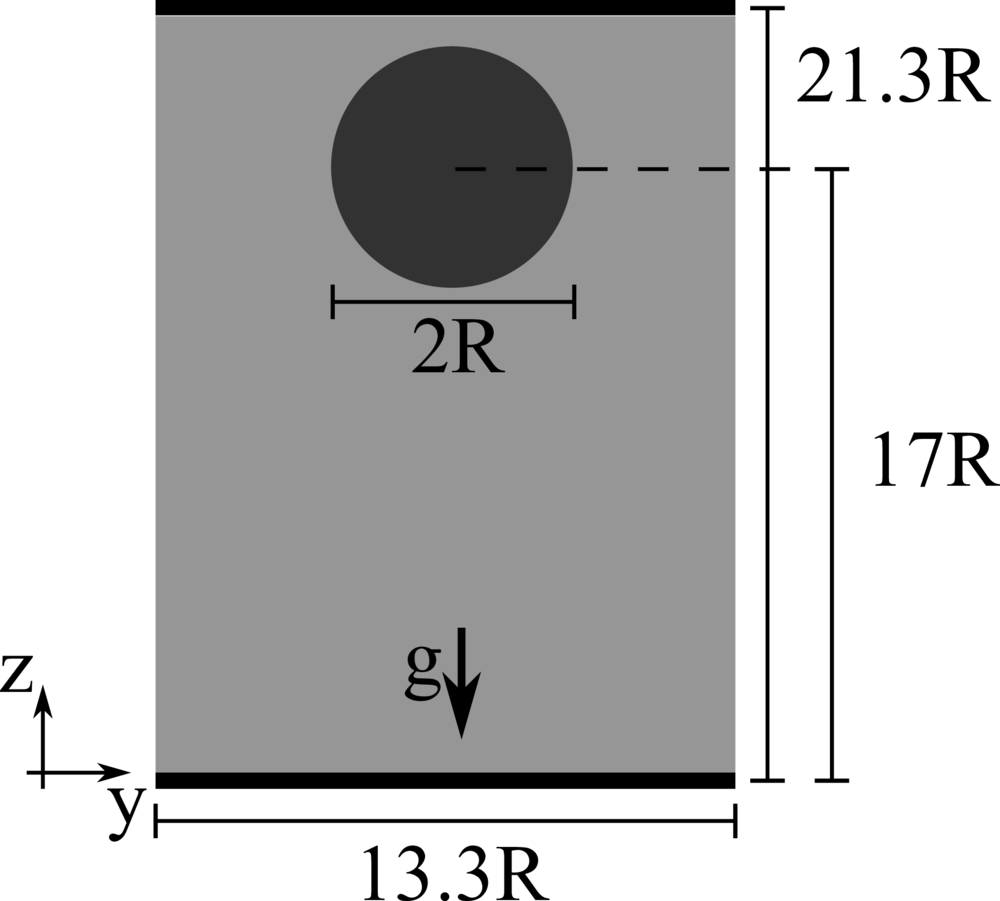
We consider a rectangular domain filled with a liquid with density and viscosity equal to \(960 kg~m^{−3}\) and \(0.058 Pa~s\). The domain size is \(0.1 m \times 0.1m \times 0.16m\) in the \(x\), \(y\) and \(z\) directions, where \(x\) and \(y\) are the two horizontal directions, while \(z\) is the vertical direction parallel to the gravitational acceleration \(g = 9.81 m~s^{-2}\). A particle of diameter \(0.015m\) and density \(1120 kg~m^{−3}\) is initially positioned at \(\left(0.05 m, 0.05 m, 0.1275 m \right)\).
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_3D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 192, nyt = 192, nzt = 304 !Size of the domain in X, Y and Z real, parameter :: lx = 0.1, ly = 0.1, lz = 0.1/192.0*304.0 !Fluid viscosity and density real, parameter :: vis = 0.058, rho = 960.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.0 !Imposed pressure gradient real, parameter :: gradP = 0.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-9.8/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 1000000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR = 0.015/2.0, ibmRhoF = rho, ibmRho = 1120.0
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.0001
initParticlePosition.dat
0.05 0.05 0.1275
References:
[1] C. H. K. Williamson. Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Physics of Fluids, 31(10):2742–2744, 1988.
[2] E. Guilmineau and P. Queutey. A numerical simulation of vortex shedding from an oscillating circular cylinder. Journal of Fluids and Structures, 16(6):773–794, 2002.
[3] J. Feng, H. H. Hu, and D. D. Joseph. Direct simulation of initial value problems for the motion of solid bodies in a newtonian fluid. part 2. couette and poiseuille flows. Journal of Fluid Mechanics, 277:271–301, 1994.
[4] T. W. Pan and R. Glowinski. Direct simulation of the motion of neutrally buoyant circular cylinders in plane poiseuille flow. Journal of Computational Physics, 181(1):260–279, 2002.
[5] A. Ten Cate, C. H. Nieuwstad, J. J. Derksen, and H. E. A. Van den Akker. Particle imaging velocimetry experiments and lattice-boltzmann simulations on a single sphere settling under gravity. Physics of Fluids, 14(11):4012–4025, 2002.



