Mini - Course: An introductory course on Knots, contact structures, and open book decompositions

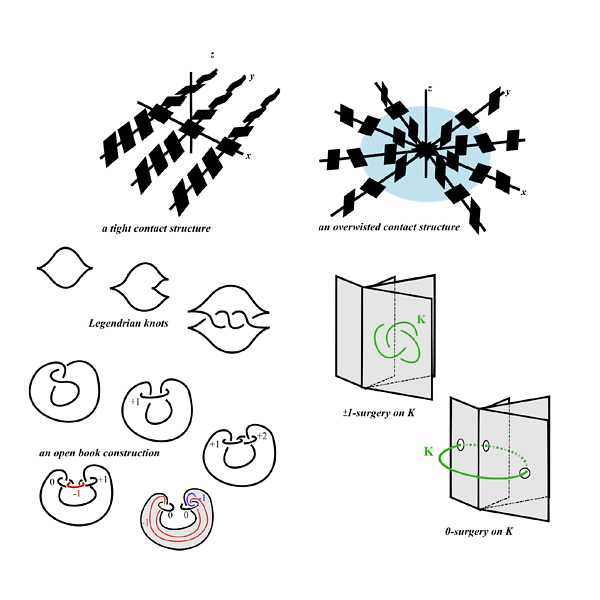
Course Description: Currently, contact geometry is a very active area of research. This course aims to introduce the basic tools to study topology and geometry of contact 3-manifolds. We will begin by highlights from knot theory. Then, we will define open book decompositions and discuss various examples in detail. We will discuss the importance of the open books in manifold theory, in particular in contact geometry. After a brief introduction on contact 3-manifolds, we will focus on a class of knots called Legendrian knots in contact 3-manifolds. We will define a new invariant for Legendrian knots using open book decompositions and discuss its applications.

Lecture I: Knot Theory basics (August 12^th, Tuesday, 13:00 – 15:00)

1. Knots and links, basic definitions

2. Isotopy of knots, Reidemeister moves

3. Seifert surfaces, framing issue

Exercises I

Lecture II: Open book decompositions (August 13^th, Wednesday, 13:00 – 15:00)

5. Definitions, examples, lots of examples: for S³, for other 3-manifolds

6. Alexander's theorem and its 3 different proof, 3 different technique (one of them is my proof)
(Alexander's theorem says every closed, orientable 3-manifold admits an open book decomposition)

Exercises II

Lecture III: Contact Structures (August 19^th, Tuesday, 13:00 – 15:00)

7. Definitions, examples: tight R³, overtwisted R³

8. Legendrian knots, transverse knots,

9. classical invariants for Legendrian knots and their calculations

Exercises III

Lecture IV: Open book decompositions and contact structures (August 20^th, Wednesday, 13:00 – 15:00)

10. Relationship between open book decompositions and contact structures

11. Invariants of contact structures from open book decompositions

12. Invariants of Legendrian knots from open book decompositions

13. Problems related to open books, invariants and contact structures

14. Suggestions to where to look.

Exercises and Open Problems IV

References:

Books:

The Knot Book, Colin Adams

Knots and Links, Dale Rolfsen

Lectures on Topology of 3-manifolds: An Introduction to the Casson Invariant, Nikolai Saveliev

An introduction to Contact Topology, Hansjörg Geiges.

Surgery on Contact 3-manifolds and Stein Surfaces, Burak Ozbagci, Andras Stipsicz

Papers:

J. B. Etnyre, Lectures on open book decompositions and contact structures, Floer Homology, Gauge Theory and Low dimensionel Topology, Caly Math. Proc. 5, American Mathematical Society (2006), 103–141.

S. Onaran, Invariants of Legendrian knots coming from open book decompositions, IMRN, (2010) Vol. 2010, No. 10, 1831-1859.